До сих пор рассматривалось состояние воды, заполняющей пористое тело полностью. При неполном насыщении вода заполняет поры частично, что приводит к образованию пленок, менисков и появлению капиллярного давления. В этой связи возникает вопрос о поверхностном натяжении и кривизне менисков, их равновесии со смачивающими пленками. Толщина смачивающих пленок определяется изотермой их расклинивающего давления, отличающейся от изотермы П(/г) плоских прослоек между твердыми поверхностями тем, что одна из поверхностей смачивающих пленок граничит с газовой фазой. Таким образом, смачивающая пленка воды представляет собой резко несимметричную систему.
Типичные изотермы смачивающих пленок воды изображены на рис. 1.6, где по оси абсцисс отложено расклинивающее давление пленки П, а по оси ординат — ее толщина H. Кривая 1 Относится к пленке воды на гидрофильной, полностью смачиваемой поверхности, а кривая 3 отвечает неполному смачиванию, когда объемная жидкость образует с пленкой конечный краевой угол. Кривая 2, в зависимости от площади* под изотермой в области П<0, характеризует либо полное, либо неполное смачивание. Вид изотермы П(/г) определяется вкладом различных составляющих поверхностных сил: молекулярных,
Рис. 1.6. Изотермы расклинивающего давления смачивающих пленок
Электростатических и структурных. Методы теоретического и экспериментального определения изотерм смачивающих пленок изложены в монографии [45].
В состоянии равновесия расклинивающее давление пленки р равно перепаду капиллярного к2 р«РРм° п давления на мениске: П = РК,
Что и позволяет определить зависимость толщины пленок от состояния заполнения пористого тела и кривизны поверхности менисков l/Rm. Как известно, PK = A/Rm, где а—поверхностное натяжение мениска.
В зависимости от Рк могут реализоваться различные состояния и, соответственно, толщины смачивающих пленок. Так, при малом капиллярном давлении (РкІ — на рис. 1.6) в зависимости от степени гидрофильности подложки могут возникать либо толстые (порядка 100 нм) устойчивые пленки (изотерма 1), либо также достаточно толстые, но метастабильные (3-пленки (изотерма 2). При приближении капиллярного давления к критическому они могут прорываться, переходя в значительно более тонкие (около 10 нм) термодинамически устойчивые ос-пленки, впервые исследованные в работе [46]. Наконец, при дальнейшем ухудшении смачивания (изотерма 3) находиться в равновесии с мениском могут только тонкие {H~ 1 нм) а-пленки. В тонкопористых телах, где капиллярное давление велико (Рк2 — на рис. 1.6), метастабильное состояние водных пленок может не реализоваться.
|
|
Вид изотерм определяется при этом не только гидрофиль- ностью поверхности, но и составом водного раствора, влияющим на электростатические и структурные силы и, в меньшей степени, на молекулярные. Так, концентрационное подавление граничных слоев (несмотря на исходно гидрофильную поверхность, например, кварца) приводит к ослаблению сил структурного отталкивания в водных пленках, что вызывает переход от изотерм типа 1 к изотермам 2 или от изотерм типа 2 к изотермам 3. Так как устойчивость толстых р-пленок определяется, в основном, электростатическими силами, изменение концентрации и состава водного раствора, влияющее на электрические потенциалы обеих поверхностей пленки, сказывается на виде изотерм П(h). При повышении концентрации электролита или (и) снижении рН уменьшаются силы электростатического отталкивания, что приводит к сдвигу изотерм П(/г)
в сторону изотермы 3. В большинстве реальных пористых тел (в силу недостаточно высокой гидрофильное™ поверхности, присутствия электролита и высокого капиллярного давления) мениски находятся в равновесии с а-пленками. Их устойчивость определяется в основном структурными силами, менее чувствительными, чем электростатические, к составу раствора. Разрушение особой структуры граничных слоев начинается при концентрации электролита более Ю-2 моль/л. В очень тонких порах гидрофильных обратноосмотических мембран полного разрушения граничных слоев воды не происходит и при более высокой концентрации раствора.
Анализ изотерм П(/г) для сс-пленок воды на поверхности кварца показал, что приближенно они следуют экспоненциальной зависимости (1.1) [47]. При этом параметр К для пленок на подложках из стекла, кварцы и слюды сохраняет примерно то же значение, что и для симметричных водных прослоек: (І-ьЗ)-Ю-4 Н/см2, но длина корреляции / выше, составляя до 10 нм для наиболее гидрофильных поверхностей и снижаясь до 1 нм при уменьшении степени гидрофильности. Повышение температуры приводит, главным образом, к падению значений I: от 3,3 нм — при 20 °С до 0,8 нм — при 40 °С для пленок на слюде. Для почти гидрофобной поверхности пиролитического углерода (краевой угол 0 = 72°) меняется, как и в случае симметричных прослоек, знак параметра К(—2-Ю3 Н/см2) при сохранении обычного порядка значений 1 = 0,7 нм.
Изменение структуры воды в тонких а-пленках на поверхности кварца подтверждено смещением полосы валентных О—Н — колебаний на 100 см-1 в длинноволновую область ИК-спектра, что свидетельствует об усилении межмолекулярных водородных связей в структуре а-пленок [45].
Равновесие менисков в пористом теле описывается обычно уравнением Кельвина, связывающим раднус кривизны менисков с давлением пара над их поверхностью. При этом не учитывается, однако, поле поверхностных сил, приводящее к изменению формы мениска, что меняет и его капиллярное давление. Точная запись условий равновесия менисков с пленками для пор в виде плоской щели имеет вид [48]:
2a + g(h,H)-G(H)
Это уравнение связывает капиллярное давление мениска Pk с шириной щели Я и толщиной пленок h, зависящей, в свою очередь, от П = Р*. Здесь g(h,H) и G(H) — избыточные удельные свободные энергии взаимодействия участков щели, покрытых пленками 1 (рис. 1.7) и заполненных жидкостью 2, соответственно. Для расчетов g(h,H) и G(H) используются изотермы смачивающих пленок П(/г) и изотермы расклинивающего дав-
///////////;///’////////и/////;///////////<///////////;//!-
|
|
|
2Н 1 { 2 |
|
I h |
Рис. 1.7. Равновесие мениска со смачивающими пленками в плоской гидрофильной щели
I J I
Ления водных прослоек П(Я) [42]. Расчеты показывают [48], что в порах шириной Н—Зч~5 нм действительное капиллярное давление на порядок превосходит рассчитанное по уравнению Лапласа (Р = 2а/Н).
При Н> 10 нм можно пренебречь в выражениях для свободной энергии членами, зависящими от Я, что приводит к более простому выражению:
|
H |
(1.3)
В котором остается только изотерма расклинивающего давления смачивающих пленок П(А). Второй член в числителе учитывает существование переходной зоны 3 (рис. 1.7) между мениском и пленкой, в пределах которой действуют как капиллярные (вследствие кривизны поверхности переходной зоны), так и поверхностные силы (локальное расклинивающее давление). Наличие переходной зоны уменьшает радиус кривизны мениска г, делая его меньшим, чем (Я—2А)/2. Так, для изотерм типа П=Л/А3 радиус кривизны мениска уменьшается до Т= (Я—3/i)/2.
При проведении таких расчетов возникает вопрос о том, какие значения поверхностного натяжения следует использовать в уравнениях (1.2), (1.3). Как известно, значения а зависят от кривизны поверхности. Однако отличия а от объемных значений обнаруживаются при г, приближающихся по порядку величины к расстояниям между молекулами. По Толмену, поверхностное натяжение вогнутого мениска должно быть для г=10 нм, примерно на 5% выше, чем плоского. Однако молеку — лярно-динамические расчеты [49] приводят к выводу о неприменимости уравнения Толмена к малым каплям жидкости (Г=2-4 нм).
Эксперименты по измерению силы F, необходимой для отрыва друг от друга скрещенных цилиндров, покрытых молекулярно гладкими листочками слюды [50], позволили осуществить проверку уравнения Кельвина. Величину F измеряли при раз
личном относительном давлении пара P/Ps. Из найденных значений F, равных 4n/?ocjcos0 (где J? o = 2 см — радиус поверхности цилиндров), определяли значения acosQ. Радиус кривизны лиенисков находили по ширине зазора между поверхностями дилиндров в зоне менисков методом многолучевой интерференции. Для воды при г>5 нм получено хорошее согласие результатов измерений с теорией. При этом использовали значение cos0=1 и объемные значения а для воды. При Pjps<0,9 и, соответственно, г< 5 нм полученные из опытов значения о cos 9 были ниже. Это снижение можно объяснить приближенным характером использованного уравнения для сил отрыва. Более — строгое выражение для F, учитывающее влияние расклинивающего давления пленок и прослоек, получено в работе [51]. Так как, по Толмену, а менисков должно быть выше объемного поверхностного натяжения, вопрос о знаке и величине отклонений ■о остается открытым. Во всяком случае, для г>5 нм можно, по-видимому, пользоваться объемными значениями а.
Для неполярных жидкостей уравнение Кельвина выполнялось вплоть до г = 0,5 нм (P/Ps = 0,1). Считается, что при этом ловышение а, обусловленное кривизной поверхности, компенсируется снижением а вследствие растяжения жидкости под действием отрицательного капиллярного давления [50].
 24 октября, 2012
24 октября, 2012  admin
admin 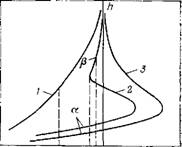

 Опубликовано в рубрике
Опубликовано в рубрике 