Поверхность реального фосфолипидного бислоя представляет собой довольно сложное образование. Граничащие с электролитом полярные головки фосфолипидных молекул образуют поверхностный слой (толщиной 0,6—1 нм), заполненный электрическими зарядами и диполями. Часть этих зарядов и диполей принадлежит самим головкам, другую часть составляют молекулы воды и ионы электролита. Поэтому термины «поверхностные заряды», «поверхностные диполи» в значительной степени условны. Заряды и диполи реальных фосфолипидных поверхностей распределены в приповерхностном слое. Происхождение такого распределения является результатом «рыхлости» поверхности, позволяющей молекулам воды и ионам электролита проникать «в глубь» поверхности.
Существенно, что, варьируя ионный состав электролита, можно менять толщину приповерхностного слоя. Например, ионы Са2+ способны вытеснять воду из области полярных головок и тем самым «сжимать» приповерхностный слой [430]. Обычно толщиной этого слоя пренебрегают и считают, что все поверхностные источники электрических полей строго локализованы на границе раздела бислой/липид, а сама эта граница считается геометрической плоскостью. Такое допущение позволяет проводить теоретический анализ электрических явлений на основе классической теории Гуи — Чепмена [431], в рамках которой структура двойного электрического слоя (ДЭС) определяется лишь поверхностными зарядами. При этом оказывается, что поверхностные электрические диполи, если они присутствуют в системе, не влияют на эту структуру. Существует целый ряд проблем, для которых предположение о локализации источников электрических полей строго на границе раздела является слишком грубым. Оказалось, что трехмерность распределения «поверхностных» электрических зарядов заметно влияет на элект-
Рис. 9.3. Модель поверхности фосфолипидного би — слоя.
А — полярная часть фосфоли — пида
Рофоретическую подвижность клеток, покрытых гликопротеи — новым слоем [426]. Таким образом, возникает необходимость детализации модели границы раздела, которую уже нельзя считать простой геометрической плоскостью.
Рассмотрим плоский диэлектрик, помещенный в водный электролит. Будем предполагать, что толщина диэлектрика много больше дебаевского радиуса электролита, что позволяет считать диэлектрик бесконечно толстым. Граница раздела диэлектрик/электролит непроницаема как для молекул воды, так и для ионов электролита. Введем де — картову систему координат таким образом, что начало координат соответствует границе раздела оси х и у лежат в плоскости диэлектрика, а ось г направлена нормально плоскости раздела (рис. 9.3). Для простоты будем рассматривать одномерную задачу и считать, что плотности источников электрических полей зависят только от г.
В полупространстве z>L находится электролит с дебаев — ским радиусом экранирования х-1, в полупространстве z<0 — диэлектрик с диэлектрической проницаемостью ет. Слой 0< <C.Z<.L заполнен электролитом и «поверхностными» зарядами с объемной ПЛОТНОСТЬЮ pf(z) и диполями с объемной плотностью
М(г). Отметим, что влияние на структуру ДЭС (на интересующих нас расстояниях) могут оказывать лишь нормальные составляющие электрических диполей, объемную плотность которой обозначим Мп(г). Влиянием латеральных составляющих можно пренебречь по двум причинам. Во-первых, обычно они значительно разупорядочены, и, во-вторых, поле, создаваемое каждым отдельным латеральным диполем, спадает по мере удаления от поверхности значительно быстрее, чем поле, создаваемое нормальными диполями.
|
|
Для липидной мембраны описываемая модель поверхности интерпретируется следующим образом. Полупространство z<О
соответствует области углеводородных хвостов, граница раздела z = 0 соответствует области глицеринового каркаса, а поверхностный слой 0<C.Z<C.L — это область полярных головок липид — ных молекул. Толщина этого слоя относительно мала (L~ нм) [423], поэтому для простоты можно считать, что все заряды и электрические диполи сосредоточены на одной поверхности, помещенной в точку Z=L. В этом случае распределение электрических источников становится «6-функциональ — ным»:
Pf(Z) = C(6(Z — L); Mn(Z)=Ifj(Z — L), (9.1)
Где At и |х — поверхностные плотности электрических зарядов и диполей соответственно; б(|)—дельта-функция Дирака.
Возникающие в такой системе электрические поля влияют на целый ряд биологических процессов. В частности, электрическое поле в полупространстве z>L определяет дальнее взаимодействие фосфолипидных мембран.
Электрическое поле определяется, как известно, уравнением
Div3=4rcp, (9.2)
Которое для рассматриваемой системы в случае классической электростатики принимает вид (используется линейное по потенциалу приближение):
4я
Ф"_*2ф=! — —[0,6(2-L)-|ie'(z-L)], (9.3)
Где е0 — диэлектрическая (статическая) проницаемость воды (е0«80). Используются обычные граничные условия
D(Q)=EmE„ (9.4)
И требование конечности потенциала при z = oo. Здесь Ет — напряженность электрического поля в диэлектрике.
Нас интересует распределение электрического потенциала в полупространстве z>L. Из (9.3), (9,4) имеем [427]:
4л Г
|
Ехр( — кг). (9.5) |
|
4xi |
^ ~ё^Г °< Ch(Xi) + Vх Sh (Xi)
Как видим, распределение потенциала вблизи гидратирован — ной (ЬФ0) гидрофильной поверхности существенно отличается от классического выражения Гуи — Чепмена:
4зх
В которое оно, однако, переходит, если поверхность становится дегидратированной (т. е. при L = 0).
Таким образом, распределение электрического потенциала вблизи фосфолипидной поверхности определяется не «истинным»
поверхностным зарядом At, а эффективным аех, который зависит как от At, так и от плотности нормальной составляющей поверхностных диполей ц и степени гидратации поверхности L. Сравнивая (9.5) и (9.6), можно определить эффективный поверхностный заряд следующим образом (для Ет = 0) [427]:
А«с=ш ch (x,L) +[лх sh (KL). (9.7)
Теоретический анализ структуры ДЭС вблизи поверхностей, источники электрических полей которых (заряды и диполи) заполняют определенный поверхностный слой, показывает, что она существенно зависит от толщины этого слоя L. Основным результатом является вывод о том, что поверхностные диполи вносят значительный вклад в электрическое поле, образующееся вблизи поверхности. Поэтому вблизи электрически нейтральной гидратированной гидрофильной поверхности существует электрическое поле, обусловленное поверхностными диполями. При дегидратации поверхности (т. е. при L->-0) это поле исчезает. Отметим, что этот результат справедлив только в рамках классической электростатики. В нелокальной электростатике поле вблизи нейтральной гидрофильной поверхности не исчезает и при ее полной дегидратации.
 24 октября, 2012
24 октября, 2012  admin
admin 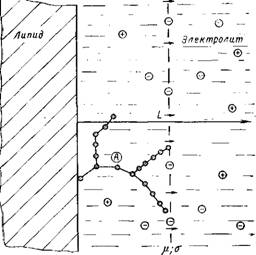
 Опубликовано в рубрике
Опубликовано в рубрике 