Когда жидкость приходит в контакт с предварительно обез — гаженной пористой средой, капиллярные силы создают давление в жидкости, которое в случае смачивания (9 < 90°) заставляет жидкость проникать в поры. Величина этого капиллярного давления согласно уравнению Юнга—Лапласа [1, 21 представляет собой произведение кривизны межфазной поверхности жидкость — пар J и поверхностного натяжения у. Когда впитывание происходит в пористой среде, где основные радиусы кривизны поверхности жидкость — пар достигают молекулярных размеров, эффект кривизны проявляется как изменение у [3—6].
От изменения у зависит время, необходимое для насыщения впитывания в пористую сферу, как результат изменения движущего капиллярного давления. Следовательно, зная уравнение скорости впитывания массы и кривизну впитываемой поверхности жидкость — пар можно определить у и результирующие эффекты кривизны из опытов по впитыванию жидкости в пористые среды, имеющие достаточно малые поры.
В опытах для определения эффекта кривизны по впитыванию жидкости пористое стекло Вайкор (Corning № 7930) было выбрано, поскольку предыдущие исследования [24, 25] показали, что для появления эффекта кривизны поры должны быть достаточно малы, но и достаточно велики, чтобы впитываемые жидкости вели себя как сплошные среды. В [24, 25 ] было найдено, что впитываемые межфазные поверхности жидкость — пар должны быть геометрическими при локальном равновесии,
изменяющимися по кривизне J в процессе впитывания. Другими словами, в процессе впитывания происходит изменение кривизны каждой межфазной поверхности жидкость — пар вдоль устойчивой лапласовой траектории [26].
В соответствии с таким динамическим механизмом впитывания жидкости было получено гидродинамическое уравнение впитывания жидкости [25] из уравнения непрерывности [27] и закона Дарси [28]. Для жесткой пористой сферы радиуса R Уравнение впитывания устанавливает связь между радиальным положением фронта жидкость — пар т] после впитывания в течение времени T под действием давления АР в форме
Зт|3 — 3R4* 4—R* — (C ДР) (2т]3 — 4^2 + 2R3) = 3k APR [2 — (с — Ь) ДР] /
Ф
Где АР = PR — Я,, = — Рт,; PR — давление при г — R (давление пара + гидростатический напор); Рл — капиллярное давление при г = т]; С — изотермическая сжимаемость жидкости; Ь — вязкостный аналог с [27]; K — кбэффициент проницаемости Дарси; Ф — пористость среды. В уравнении ^1) величины Ь и с вносят поправку в уравнение течения на вызываемые давлением изменения вязкости и плотности жидкости и определяются следующими уравнениями
|
(2) (3) |
|
Р= р0 ехр'(— М — = М-о ехр (—ЬРЦ) |
Где р0 — плотность жидкости при г = R; Р — плотность жидкости при г = г);
Ро — вязкость жидкости при г = R; Р. — вязкость жидкости при Г = ‘П.
В полном опыте по впитыванию жидкости радиальное положение т] фронта жидкость — пар исчезает за конечное время Tx. Если эти конечные условия, т. е. Tj = 0, когда T = налагаются на уравнение впитывания, выражение, связывающее время насыщения впитывания tx с капиллярным движущим давлением Рч, дает:
R*(l+2cP1l) = ^-l(b-c)P1l-2]tl (4)
Разделив обе части уравнения (4) на член в квадратных скобках в правой части уравнения, опустив члены с Рч* поскольку члены второго и более высоких порядков по не были использованы при выводе уравнения (1) [24, 251, и
решив относительно получим:
TOC o "1-3" h z Р________________ 2Ф*2 (5)
11 ~ 2ktx — f Я2ф (b + Зс)
Исключение капиллярного движущего давления Рп объединением уравнения (5) с уравнением Юнга—Лапласа [1, 2]
Л, = YJ ‘ (6)
Дает соотношение между у и параметрами эксперимента по впитыванию:
1
2Ф** 1 (7)
12kh + ФR% (Ъ + Зс)
Если бы были оценены все восемь неизвестных уравнения (7), можно было бы рассчитать зависящую от кривизны величину у.
Однако параметр межфазной толщины является более фундаментальной мерой эффекта кривизны, так как он в принципе не зависит от J [15, 30, 311. Этот параметр определяется [10] как
Б = к (Г = 0) — к (Cs = 0) (8)
Где X (Г = 0) — главный радиус кривизны эквимолярной
Разделяющей поверхности, расположенной при Г = 0;
X (Cs = 0) — главный радиус кривизны поверхности натяжения, расположенной при Cs = 0;
Cs — коэффициент при D.J в термодинамическом уравнении Гиббса [3 ].
Уравнение Толмэна [10]
Y=yto(l-&/) (9)
Есть уравнение связи б и у.
Исключение у в уравнениях (7) и (9) и решение относительно 6 дает:
С _}_ ,________ 1__ Г__________ 2ф#2 I
J + Yj* L 12&*! — j — ф/?2 (B — j — Зс) J
Шесть из восьми переменных правой части уравнения (10) ("Уоо, ф, R, Tly B и с) могут быть или измерены, или легко получены из других литературных источников. Однако остающиеся два (K и J) требуют независимого измерения, которое должно быть исследовано далее.
Коэффициент проницаемости Дарси K определялся из данных по скорости проницаемости жидкости, полученных при использовании уже описанной техники. Для стационарного осевого течения жидкости через круговое сечение пористого диска площади А и толщины L под действием давления PL Объем протекшей жидкости Q в соответствии с законом Дарси равен:
Q=kA-^~ (11)
Решение относительно K дает
QL
* = (12>
Откуда K может быть рассчитано непосредственно из данных по скорости протекания жидкости.
Множество отдельных межфазных поверхностей жидкость — пар, которые в процессе впитывания жидкости постоянно изменяются как по размеру, так и по числу являются во все моменты времени поверхностями постоянной кривизны J [24, 25]. Эти отдельные межфазные поверхности жидкость — пар проходят через все поровые пространства, и, следовательно, капиллярная движущая сила для впитывания жидкости зависит от среднего поперечного размера поры.
Два обычных метода для измерения таких размеров, а именно: определение изотерм сорбции и ртутная порометрия, неприменимы в мезопорах, так как они зависят от эффекта кривизны.
Стационарное кнудсеновское течение газа (СКТ) [32] не зависит от этого эффекта, но, главным образом, зависит от среднепоровых сужений или шеек. Поэтому была разработана другая методика, основанная на опытах по кнудсеновскому течению газа, которая измеряет средний размер полного поперечного сечения поры.
Рассмотрим поровую систему, показанную на рис. 3. Если на концы капилляра мгновенно подать давление газа Р — = Р0 и Р = 0, получится неустановившееся течение газа *. В процессе неустановившегося кнудсеновского течения (НКТ) в каждой поре молекулы газа, которые входят через каждую шейку поры в примыкающее поровое тело, не будут зависеть от соседних молекул, .как устанавливается диффузионной теорией Кнудсена [33]. Тем не менее чистое направление молекулярного полета будет неизбежно иметь радиальную составляющую, вызванную заполнением молекулами газа радиальных краев перовых пространств. Это проиллюстрировано
* Для этой методики должны выполняться три требования к условиям течения газа: время, которое молекулы газа проводят в адсорбированном состоянии, должно быть коротким в сравнении со временем, проводимым в газообразном состоянии; перенос газовой фазы должен быть в кнудсеновском режиме и квантовые эффекты должны быть очень незначительны.
|
Гр — радиусы поры в любой точке вдоль оси поры; гс— средний радиус кривизны поверхности постоянной средней кривизны, отступающей от стенки поры; гп— гидравлический радиус шеек или сужений пор; гр— угол между стенкой и осью поры. |
На рис. 3. Когда достигается СКТ, чистое радиальное течение молекул газа исчезает. Результат такого поведения состоит в том, что в условиях НКТ процесс радиального течения газа зависит от объема поры. При СКТ на течение газа влияют только шейки поры [32].
Теперь может быть разработан метод определения средней межфазной кривизны поверхности жидкость — пар в пористых средах, основанный на экспериментальных данных по НКТ и СКТ.
Поскольку СКТ зависит от размеров шейки поры, а НКТ — от общих размеров поры, т. е. размеров порового пространства и поровой шейки, уравнения течения требуют различных определений пористости (отношение объема пустот к общему объему пористой среды). Концепции СК-пористости (q>s) и НК-пористости, ((ft) для кнудсеновского течения были впервые введены Гуднайтом и др. [34, 35]. Используя уравнение Бар-
Поверхностное натяжение и кривизна | 255 рера для времени запаздывания [36] для НКТ, можно записать
Где TLB — отрезок, отсекаемый на оси абсцисс данными СКТ по зависимости объема перенесенного газа от времени (барреровское время запаздывания); т — извилистость поровой среды; L — толщина поровой среды (одномерное течение); D — коэффициент диффузии. Из выражений, полученных для ф5 и <р, в жесткой изотропной пористой среде в Приложении для пористости при нестационарном и стационарном кнудсеновском течении газа [34, 35] следует
72
Ф< _ г_с
Ф* 7
Где гс — средний радиус кривизны для всех пор;
Гп — средний гидравлический радиус поровых шеек, или
Сужений. Уравнение (13) принимает вид:
T2L2~r2
= (15)
|
=- (14) П |
Если течение кнудсеновское, из газовой кинетики следует выражение для коэффициента диффузии
|
27n(8RT_T 3 nMw |
|
D = |
У (16)
Что при сочетании с уравнением (15) дает:
_2 J 2~2 1 Т L гс ( NMw — г
Т Т L RC ( NMw —
Tlb = ~A(17)
^ п
{R — универсальная газовая постоянная; Mw — молекулярная масса жидкости).
Решение относительно гс дает:
Г — г f*TLB?n(.*RT
Rc~rny x2L2 ^ nMw ) (18)
Извилистость, как это следует из написанных выше уравнений для изотропных пористых сред, равна (обсуждение
(19)
Межфазную кривизну поверхности жидкость — пар J можно тогда определить как
2 а J = — =—- cos 9
Rc~t О
Где TQ — толщина неподвижной адсорбированной пленки непосредственно перед границей жидкость — пар [24, 25].
Переменные в уравнении (20) могут быть определены из опытов по СКТ и НКТ [24, 25, 34, 35, 36].
 2 января, 2013
2 января, 2013  admin
admin 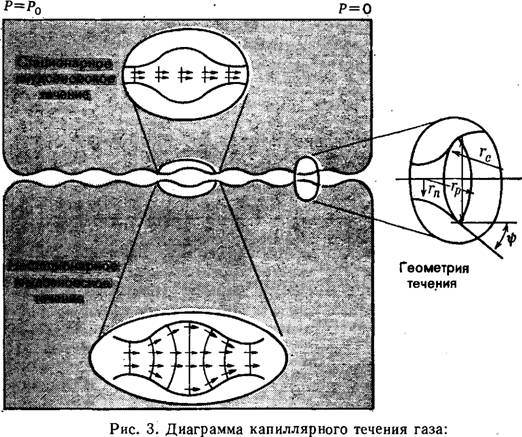
 Опубликовано в рубрике
Опубликовано в рубрике 