Установленные соотношения статистической механики позволяют дать ответ на центральный вопрос о дисперсионных силах в конденсированных системах. В наиболее общем виде этот вопрос может быть поставлен так:
Требуется найти потенциал взаимодействия двух молекулярных тел любой природы, формы и размеров, находящихся в жидкой или газообразной среде произвольного состава.
Поскольку речь идет о дисперсионных силах, то имеется в виду, что тела находятся друг от друга на расстояниях, много превышающих размеры отдельных молекул.
В дальнейшем понадобится знать явно лишь дисперсионную составляющую парного эффективного межмолекулярного потенциала, которая и начинает доминировать на больших расстояниях. Учитывая, что характер зависимости этой составляющей от расстояния такой же, как и в газах, можем написать для нее выражение:
Ф(/, i) = — ASjSr^ (12)
Здесь As.S. — силовая постоянная;
-> -» 1
Гц = | rt—Гу | — межмолекулярное расстояние; подразумевается, что параметр "К принимает значения 6 или 7 для обычных или запаздывающих дисперсионных сил.
В обоих из указанных случаев ради краткости используется единое обозначение для силовой постоянной. Надо помнить, однако, что при этом она имеет различные значения и даже размерности.
Очевидно, что взаимодействующие тела — будем их называть тело 1 и тело 2 — можно в общем случае понимать как молекулярные комплексы {%} и {п2. Систему же из тел 1 и 2 можно понимать как молекулярный комплекс пх-{-
Искомый потенциал взаимодействия тел 1 и 2, который будем обозначать через W12, представляет собой потенциал средней силы. Как известно, последний непосредственно связан с функциями распределения статистической механики. В рассматриваемом случае взаимодействия двух тел эта связь может быть записана в виде соотношения
Фи = ~ З"11" [Р ("1 + «Л/Р W Р {"2}] (13)
Которое следует из определения (4) для функций распределения и из их смысла как вероятностей распределения молекул.
В интересующей области больших расстояний между телами можно использовать метод асимптотической оценки диаграмм [7—9] полученного ранее (стр. 173) разложения для функции распределения р пх + П2.
Очевидно, что во всех диаграммах, кроме сводящихся к произведению р {tlx] р {п2у будут обязательно содержаться малые множители в виде растягивающихся — по мере удаления тел друг от друга — майеровских связей. Главный вклад при этом будут давать диаграммы с минимальным числом растягивающихся связей. Это диаграммы, которые могут быть разделены на две части, с одним из комплексов {я^ и |п2| в каждой, удалением одной майеровской связи. В данных диаграммах по мере неограниченного удаления тел друг от друга может растягиваться всего одна — именно указанная связь. И когда растягивается только она одна, данные диаграммы и оказываются асимптотически существенными.
|
(14) |
Результат суммирования асимптотически существенных диаграмм может быть наглядно представлен соотношением:
Р{п1+п2}=р{п,}р{п2}+
{п,} {Л2}
Изображенные здесь блоки обозначают суммы диаграмм в разложениях р {я^ и р {/г21; линия обозначает растянутую
Майеровскую связь / (1, 2) = Ms, s/концы 1 и 2 этой линии могут подсоединяться к любой из вершин соединяемых ею блоков.
Поочередное подсоединение линии к различным вершинам блоков можно в функциональном методе эффективно учесть домножением концов линии на операторы £ (1)б/б£ (1) и £ (2) б/б£ (2) с последующим интегрированием по всем значениям аргументов 1 и 2.
|
(15) |
Действие данных операторов на функции pj^} и р{я2| легко находится с помощью функционального представления (5) для этих функций:
|
|
= £ в(1. О Р <«L) + Р <«1 + l}-p{"L}p(l)
Здесь I характеризует вершины блока (л^, б (1, I) — обычная б-функция по непрерывным переменным и символ Кроне — кера — по дискретным.
Дисперсионные взаимодействия в капиллярных системах | 177
С помощью обозначения
Ар<м{*!})= Seo; О+ ^„j1* -Р(О (16>
Полученный результат записывается в виде
СО) у Р К) = Р Ы Ар (1|{я,)) (17)
И аналогично для функции р |л2}.
Очевидно, р пх + 1}/р представляет условную одно — частичную функцию распределения в поле комплекса пх}. Поэтому определяемая соотношением (16) функция Лр (1 | пх}) представляет избыточную одночастичную функцию распределения в присутствии тела 1 — избыточную по сравнению со случаем, когда это тело отсутствует.
Подстановка соотношения (14) в формулу (13) с учетом (17) и аналогичного равенства для функции р {/г2| приводит (после разложения логарифма в ряд и удержания главных по дисперсионному взаимодействию членов) к следующему важному результату [22]:
^12 =~ 2 J^Aps (‘li{«l»X
X £ J^A^f/i^Vlf (18)
T ‘
В полученной формуле выполнено интегрирование по уг-
Ловым координатам молекул. Соответственно Др5 (гх [ {rtjj)
И Др, (г2 | представляют обусловленные наличием взаимодействующих тел избыточные локальные плотности компонен-
Тов s и T в точках гх и г2. Множитель Astrn описывает взаимодействие отдельных избыточных молекул в данных точках. Интегральный вклад взаимодействий берется по всем областям Vi И V2, в которых избыточные локальные плотности эффективно отличны от нуля.
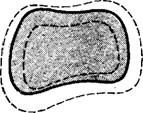
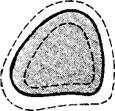
На рис. 1 сплошными линиями обозначены граничные поверхности взаимодействующих тел. Внешние и внутренние
|
Рис. 1. Поверхностные слои взаимодействующих тел. |
Штриховые линии указывают эффективные границы прилегающих поверхностных слоев со стороны среды и тела. Области, окруженные внутренними штриховыми линиями, соответствуют объемным состояниям тел. В телах микроскопических размеров эти области практически не реализуются. Области V и V2, дающие вклад во взаимодействие, лежат внутри внешних пунктирных линий. По этим областям и ведут интегрирование в формуле (18).
Общность и наглядность выражаемого формулой (18) результата позволяет назвать его принципом взаимодействия. Словами данный принцип формулируется так:
Два любых молекулярных тела в произвольной жидкой или газообразной среде взаимодействуют так, как взаимодействовали бы эти тела в вакууме, если бы в них и окружающих их поверхностных слоях локальная плотность каждого компонента отсчитывалась от ее значения в однородной среде в отсутствие тел.
Установленный принцип полностью решает главную проблему взаимодействия, заключающуюся в определении влияния, которое оказывает на взаимодействие среда, реально окружающая тела. Действительно, формула (18) учитывает как эффекты последовательной передачи сил молекулами среды, которая при этом меняет свою структуру и образует вокруг тел сольватные или адсорбционные слои, так и эффекты передачи сил, связанные с перестройкой самих взаимодействующих тел (образованием у тел собственных поверхностных слоев).
|
|
Достигнутая в принципе взаимодействия формальная аналогия с гидростатическим законом Архимеда объясняется тем, что в случае дисперсионных сил посредником взаимодействия тел оказываются лишь близко лежащие к ним молекулы среды. В случае электрических сил данная аналогия исчезает. Так, в случае дипольных сил линию, 2 в диаграммном
(19)
Где блоки, в свою очередь, изображают суммы диаграмм в разложениях р (0, р (/)-.., а линии по-прежнему обозначают растянутые майеровские связи.
Представленные в (19) диаграммы описывают взаимодействия с участием далеких молекул среды, лежащих от тел на расстояниях, превышающих молекулярные размеры. Учет таких взаимодействий требует введения дополнительных коэффициентов, связанных с диэлектрической проницаемостью среды [22].
 1 января, 2013
1 января, 2013  admin
admin 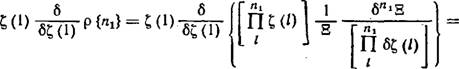
 Опубликовано в рубрике
Опубликовано в рубрике 