Рассмотрим теперь случай, когда радиус кривизны граничной поверхности — обозначим его через а* — принимает конечные, однако все же настолько большие (по абсолютной величине) значения, что а* > H. При этом расстояние H сохраняет прежний порядок величины.
Имеются в виду как вогнутые, так и выпуклые поверхности. Поэтому радиус кривизны поверхности, а также и ее главные радиусы кривизны могут принимать как положительные, так и отрицательные значения.
В соответствии со сделанными допущениями будем теперь также учитывать члены порядка H~K+3H/A*. Величинами 0 (H~:И-1), как и прежде, будем пренебрегать. Кроме того, пока будем пренебрегать величинами 0 (H~^+3H2La*2) и 0 (H~^+2H/A*). В пределе а* —> оо результаты этого раздела перейдут в результаты для случая плоских поверхностей.
Вместо формулы (39) мы будем теперь иметь [25, 26, стр. 182]:
РМ = р«" М + (х-^-з, [‘ + и х
Х 2 л* W> — рм+т^ 2-а®*
S f t S J t
(43)
Как и в случае плоских поверхностных слоев, с помощью (43) легко получить соответствующие формулы для полной локальной плотности и локального состава. Можно получить с помощью (43) также и формулу для локального тензора давлений.
Очевидно, тензор будет диагонален в криволинейной системе координат с началом в точке наблюдения, с ocbioZ, перпендикулярной к граничной поверхности, и с осями X, Y Вдоль главных направлений этой поверхности (в точке пересечения ее осью Z).
Данная криволинейная система X, Y, Z представлена на рис. 2. Линиями изображены главные направления граничной
H
|
СЦх) Рис. 2. Характеристики искривленной поверхности. |
Поверхности в точке, в которой поверхность пересекается с осью Z. Эти главные направления ломечены соответствующими им главными радиусами кривизны поверхности ах и ау. Указано также расстояние H от точки пересечения граничной поверхности осью Z до начала криволинейной системы координат X, Y, Z. Это начало совмещено с точкой наблюдения.
Приведем конечный результат расчета диагональных составляющих тензора давлений в указанной криволинейной системе координат [25, 26]:
= + (Х-^-4) £ S м» — рН <44>
|
Z |
|
Y |
S, t
|
2я |
|
Рхх — + (А> _ 2)2 . (А — 3) H |
.Fc—M-з
2 (А,— 4) ах
|
2(1-4) ау |
Г-^Р?0 [р}р)-р}а)] +
S. t
(45)
|
S, t Fc-JH-3 |
|
УУ + |
2я
(А, — 2)2 (А — 5) H
2 (А — 4) A^J
S. t
1 , Fr-з) А,
+ 2(1-4) ах
[P}p>-pje)] +
|
(46) |
+ 2(ЯА-Т)23) I^PW’
S, *
В отличие от функций распределения и нормальной составляющей тензора давлений Рп — PZzy его тангенциальные составляющие Рхх и PYY. зависят не только от радиуса кривизны поверхности а*, но и от ее главных радиусов кривизны ах и ау. Разумеется, из этих трех переменных, задающих геометрию поверхности, независимыми являются только две, поскольку,
2 1,1
Как известно, —— — Н————- .
А* ах ау
Выражения (45) и (46), очевидно, симметричны относительно замены ак на ау и ау на ах.
В то время как в выражениях для функций распределения и тангенциальных составляющих тензора давлений член порядка fo-M-зfr/a* ИГрает роль поправочного по отношению к главному члену порядка /1_я-+3, в выражении для нормальной составляющей тензора давлений этот член является главным. Действительно, в соответствии с формулой (41) отличие нормальной составляющей тензора давлений от давления в фазе а может быть вызвано лишь наличием кривизны граничной поверхности.
Значительно сложнее, чем в плоском случае, проводится проверка формул (44)—(46) для тензора давлений на согласование с условием механического равновесия. Обращаясь к этому важному вопросу, рассмотрим предварительно два частных случая: цилиндрическую и сферическую граничные поверхности.
В случае цилиндрической поверхности мы имеем ах — оо, Ау = а, где а — радиус цилиндрической поверхности и ось X Выбрана параллельной ее оси.
Обозначим тангенциальную составляющую Рхх через Ptl, А тангенциальную составляющую PYY через Р(2. Можно показать, что условие механического равновесия (10) для систем цилиндрической симметрии имеет вид
1р(грп)=р<. <47>
Где г — расстояние точки наблюдения тензора давлений до оси цилиндрической поверхности.
Подставляя (44) и (46) в равенство (47), убеждаемся, что постоянные члены, а также члены порядка /r-M-з в его левой и правой частях совпадают. Что же касается членов порядка H~K+3H/A и то они содержат вклад от неизвестных членов
В Рп порядка h-*+3h2/a2 и H~^+2H/A.
Мы можем, очевидно, использовать равенство (47) для определения этих неизвестных членов. В результате вместо (44) будем иметь в рассматриваемом случае цилиндрической
194 | Ф. М. Куни, А. И. Русанов
Граничной поверхности [25; 26, стр. 182]:
^(Х — 2)*(1 — 4) а + 2 а2 / Л
S, t
(48)
Аналогично рассматривается случай сферической поверхности. Имеем ах = ау — а, где а — радиус сферической поверхности. Тангенциальные составляющие Рхх ® ^Yy теперь совпадают: РХх = PYy = Ри а условие механического равновесия (10) имеет вид
-IF (r2pn) = pt №
Где г — расстояние точки наблюдения тензора давлений до центра сферической поверхности.
Равенство (49) может быть использовано как для проверки правильности уже найденных членов в (44)—(46), так и для определения неизвестных поправочных членов к Рп. С учетом этих поправочных членов будем иметь в рассматриваемом случае сферической граничной поверхности [25; 26, стр. 182]:
Р _ р«*> . 4я Л-М-з / JL Л. 2 — х
(Я — 2)2 (К — 4)
В общем случае слабо искривленной поверхности произвольной формы условие механического равновесия (10) имеет вид:
~ ^-hl^-h) Ж IK — H) (% — H) рп] —
РхК +-AV (51)
Ах — h Uy — h
Как и в разобранных выше частных случаях, равенство (51) может быть использовано, с одной стороны, для подтверждения правильности уже найденных членов в (44)—(46), а с другой стороны, для отыскания высших поправочных к Рп. Уточнен-
Ное таким способом выражение для нормальной составляющей тензора давлений принимает вид [25; 26, стр. 182]:
H-w(JL + JL 2^p(«>r}«*> (52)
|
Х°У ) S, t |
|
Рп = р<а> + |
|
(К-2) |
|
|
ах ау / .
Представленные в этом и предыдущем разделах результаты наших исследований молекулярной структуры в системах с плоскими и слабо искривленными граничными поверхностями в течение ряда лет оставались достоянием только микроскопической теории. Лишь совсем недавно [31, стр. 26] аналогичные исследования были проведены и на основе макроскопической теории дисперсионных взаимодействий [1, 2]. Объектами этих исследований были локальная плотность и тензор давлений. Полученные в главном асимптотическом члене (который только и рассматривался в [31, стр. 26]) зависимости данных величин от расстояния до граничной поверхности и от ее кривизны совпадают с приведенными выше.
 1 января, 2013
1 января, 2013  admin
admin 
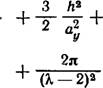
 Опубликовано в рубрике
Опубликовано в рубрике 