|
177" |
При обменной молекулярной адсорбции из растворов происходит перераспределение компонентов между объемом раствора и поверхностным слоем. Обмен одного компонента в объеме
12 Фролов ю. Г.
Раствора или поверхностном слое на другой можно представить как квазихимическую обменную реакцию между компонентами В (компонент /) и С (компонент 2) с константой обмена Ка
В + С С + В: к„ = а2а,/(а, а2) НИ.102)
Где В и С — компоненты, находящиеся в поверхностном слое; о,- и и,— активность компонентов в поверхностном слое и объеме соответственно.
Если выразить активность компонентов через молярную долю х и коэффициент активности у, то уравнение (III.102) примет вид
XnXi У, у. х, х,
(III.103)
■*1*2 V1V2 Х1х.2
Где K^ — коэффициент, учитывающий изменения коэффициентов активности с изменением состава раствора (их отклонения от единицы); К—концентрационная константа обмена.
Константа К равна
К=х2х ,/(.FlA-2) =D2/DI (III. 104)
Где Di = Хі/Хі — коэффициент распределения компонента между поверхностным слоем и объемом раствора; .Г,-, х,- — молярные доли компонента в поверхностном слое и в объеме раствора.
Выразим молярную долю компонента / через молярную долю компонента 2 (,v,—J—X2= 1), тогда уравнение (III.104) примет вид
Ха(1 — х2)
(1 — хГ)хг
Из этого уравнения найдем молярную долю компонента 2 в поверхностном слое:
| + С"-105)
Уравнение (III. 105) называют общим уравнением изотермы адсорбции из бинарных растворов с константой обмена. Константа К является также коэффициентом разделения компонентов 1 и 2, т. е. отношением коэффициентов распределения второго и первого компонентов (III.104). Концентрационная константа обмена равна термодинамической константе обмена Ка только при условии /С, = 1 (111.103). Если коэффициенты активности компонентов и соответственно Л’т изменяются при изменении состава раствора, то не останется постоянной и К (III.103). Выражение концентраций в молярных долях позволяет графически представить изотерму при всех соотношениях компонентов, даже для неограниченно смешивающихся веществ (рис. III.16).
Проведем анализ зависимости (III. 105). Если л’2—>-0, то при любом значении К в знаменателе уравнения (III.105) можно пренебречь величиной (К~)х2, и тогда изотерма приобретает вид закона Генри:
Хг=Кх 2 (III.106)
Поэтому в начале изотермы наблюдается линейная зависимость х2 от х2. При К> 1 изотерма идет выше диагонали (рис. 111.16, кривая /), при К< 1 — ниже диагонали (рис. III.16, кривая 2), при К= 1 — по диагонали.
Проанализируем ход изотермы адсорбции из растворов с ростом концентрации при 1 и /С<СІ. При таких условиях можно не учитывать влияние изменения Kv Если 1, то разность (К—1) имеет положительный знак и уравнение (III. 105) принимает вид, аналогичный уравнению Ленгмюра:
Ь^ТГкЪ <ш-107>
Где К’^К при Д’»1.
Из соотношения (III.107) следует, что знаменатель растет ■с увеличением концентрации компонента 2 в объеме, и первоначальный прямолинейный участок зависимости х2 от х2 переходит в кривую выпуклой формы — рост величины адсорбции замедляется с увеличением концентрации компонента в объеме (рис. III.16, кривая /).
|
|
|
|
|
Рис. III. 16. Изотермы адсорбции из бинарного раствора в соответствии с уравнением (III. 105): I —К>1; 2—К<1; 3— иллюстрация адсорбционной азео — троиии |
Если К< 1, то разность (К—1) приобретает отрицательный знак и уравнение (III. 105) переходит в соотношение:
|
(III.109) |
|
12 |
|
179 |
Следовательно, при увеличении концентрации компонента 2 в объеме знаменатель уравнения (III.108) уменьшается и более быстро возрастает величина адсорбции (см. рис. III.16, кривая 2). Зависимость приобретает вид вогнутой кривой. Изотермы при К> 1 и К< 1 сходятся в точке, для которой справедливо соотношение
Х2 = х2 = 1
Оно также следует из уравнения (III.105).
|
(III. 112) |
Если константа /( мало отличается от единицы, т. е. величины сродства компонентов к адсорбенту близки, то на форму изотермы могут влиять изменения коэффициента Кт Наиболее интересной зависимостью является изменение знака величины (К—1) с изменением состава раствора. Например, при малых концентрациях изотерма может проходить выше диагонали, а при больших — ниже ее, пересекая в точке К= 1. Это соответствует проявлению адсорбционной азеотропии.
Молярные доли компонентов в поверхностном слое практически определить так же трудно, как и абсолютную величину адсорбции А. Если один из компонентов адсорбируется значительно лучше другого, то можно принять величину адсорбции А равной величине гиббсовской адсорбции Г. Последняя, как уже упоминалось, экспериментально определяется по разности количеств.! вещества в объеме до и после адсорбции [см. уравнения (II.49) или (111.99)]. Если компоненты близки по адсорбционной способности, то для определения величины адсорбции А можно воспользоваться уравнением, связывающим величины Л и Г (III.100), а также соотношением (111.105). Соотношение (III.105) можно записать относительно величины адсорбции А, если учесть, что
At + A2 = ns, .r, = -4,/ns, ,r2 = A2/ns (111.110)
Тогда для второго и первого компонентов соответственно имеем:
Nskx2 nsx i
1 4- (К — 1)Х2 • А1 " 1 4- (К — 1 )хг (ш-т>
Подставляя эти выражения в уравнение (111.100) найдем:
П0Д хг Nsxtx2(K — 1) S ~ 1 4- (К — 1)*г
Для удобства обработки экспериментальных результатов полученное соотношение записывают в линейной форме:
Sxtxa 1 1
+ — (Ш’"3)
Линейная зависимость в координатах s• хіх2/(П0ІХІ)^-ХІ позволяет определить графически величины ns и К, а используя уравнение (III.111), можно рассчитать А2 и построить изотерму адсорбции A2 = f(x2).
 2 ноября, 2012
2 ноября, 2012  admin
admin 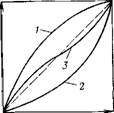
 Опубликовано в рубрике
Опубликовано в рубрике 