Уравнение Ленгмюра можно использовать только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. Это условие выполняется достаточно строго при хемосорбции, физической адсорбции газов при небольших давлениях и температурах выше критической (в отсутствие конденсации на поверхности адсорбента), а также при адсорбции из растворов. Указанное ограничение для применения уравнения Ленгмюра связано не столько с формальным описанием адсорбции, сколько с невозможностью получить правильные значения параметров К и А^, соответствующих их физическому смыслу.
В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться па второй, третий и последующие адсорбционные слои. Эта возможность реализуется, когда газы и пары адсорбируются при температурах ниже критической. В этом случае образуются полимолекулярные слои вещества на поверхности адсорбента. Полимолекулярную адсорбцию можно представить как результат вынужденной конденсации пара под действием поверхностных сил. Если в области образования мономолекулярного слоя величина адсорбции существенно замедляет свой рост с увеличением давления пара, то в области давлений, близкой к давлению насыщенного пара, она резко начинает
Рис. Ш.6. Изотерма полнмолекулярной адсорбции
Возрастать и адсорбция заканчивается объемной конденсацией пар:-) при P = Ps (рис. III.6J.
Первые попытки получения уравнения изотермы полимолекулярной адсорбции были сделаны еще Ленгмюром. Современная форма уравнения полнмолекулярной адсорбции — основного уравнения обобщенной теории Ленгмюра — была предложена лишь примерно двадцать лет спустя Брунауэром, Эмме- гом и Теллером. В соответствии с начальными буквами фамилий авторов обсуждаемая теория получила название теории БЭТ. В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата. Тогда процесс адсорбции можно представить в виде последовательных квазихимических реакций:
|
К„ |
|
Кг’- |
|
К, |
А + В ^ АЁГ: ХВ + В АВ2: АВ2 + В ^ АВ3 и т. д.
Константы равновесия этих реакций соответственно равны IABJ,, |ДВ2| ^ (АВ3 ]
|
А0Р |
IАВ] р’
И т. Д-
|АВ.21р
Где А о—концентрация свободных адсорбционных центров.
Из представленных уравнений получаются следующие выражения для концентрации соответствующих комплексов на поверхности адсорбента:
[АВ] = К,,Аар
[АВ2]=Д’,{АВ]р= VCA, P2 (111.28)
IА Вз] = К2 [А В21 р = К„ К, К2А „р3
Авторы теории БЭТ приняли, что во всех слоях, кроме первого, взаимодействуют между собой в основном молекулы адсорбата, как и при конденсации. Поэтому было принято, что
Д’, =/С2= … =/cL=fl„;/fl„ = i/Ps H1J.29V
Где Ki. — константа конденсации пара, равная отношению активностей вещества в жидком состоянии аж и в состоянии насыщенного пара а„, принято йж = 1 (стандартное состояние), а а„=р…
|
|
Для упрощения вывода и вида конечного уравнения полимолекулярной адсорбции введем обозначения:
|
К,, |
|
1 |
|
PjPs — |
|
Kl PS |
|
Рь |
(III. ЗО >
Постоянная С равна отношению констант равновесия адсорбции (мономолекулярной) и конденсации пара. Логарифми рование этого отношения приводит к разности логарифмов констант, а из этого следует, что постоянная С характеризует разность энергий Гиббса процессов адсорбции и конденсации, т. е. энергию Гиббса чистой адсорбции:
— AG°=RT In С =RT In К„ — RT In Л"с
Учитывая уравнения (III.29) и (III.30), получим из уравнения (III.28).
[АВ„] =KPKLn-,A0p» = CKLnA0p" = = СА^р/р,)" = СА0х"
Или
[АВ] =А0Сх [АВ2]=Л0С.Г2; [АВ3] = Д0СЛ‘3 … и т. д.
Общее число активных центров на адсорбенте, или емкость монослоя, будет равна
Л«=Л0+[АВ] + [АВ21 + [АВ31+ … =
= Л0 + Л0СХ + Л0С. Ї2 + Л0СЛ-3 + …= = Д0[1 + Сл:(1+.Ї + .Ї2+ …1]
Ряд в круглых скобках (1+х-(-х2-|-…) является геометрической прогрессией, сумма членов которой равна 1/(1—х) при условии х<1. Поэтому
А _А ( Сх_М1+Сх-х) + [ _ х J— (1-х)
(III.31)
Величина адсорбции компонента В равна
Д = [АВ] + 2[АВ2] + 3[АВ3]+ … = = А0Сх + 2А0Сх2 + 3 Л 0Cx3 +• … = = А0Сх(1 + 2х + 3х2 + …)
Ряд (1+2*+Зх2+…) является производной по г предыдущей геометрической прогрессии, и сумма ее членов равна 1/(1—Х)2. Поэтому
|
(1-х)* |
А0Сх
(III.32)
Подставляя значение А0 из соотношения (III.31) и выражение для х (ПІ.30), окончательно получим:
A_,CpiPs
(III.33)
(і — РІР$)[ і + (С — i)p/psl
Соотношение (III.33) является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимоле
кулярной адсорбции БЭТ. С уменьшением давления при P/Ps<.
1 уравнение БЭТ превращается в уравнение мономолекулярной адсорбции Ленгмюра, которое при дальнейшем уменьшении давления (р—>-0) переходит в закон Генри. Например, при P!Ps<СІ имеем из уравнения (III.33):
■4 Ср/р, A^KpPsp/ps крР
Д •= 1 + Cplps " 1 +- Kppsp/ps 1 + Кгр
При обработке экспериментальных результатов уравнение БЭТ обычно используют в линейной форме:
Phh І С— І
___e__+__p/pf (II1.34)
Уравнение (III.34) позволяет графически определить оба постоянных параметра Ах и С (рис. III.7). Отрезок, отсекаемый на оси ординат при экстраполяции зависимости, представленной на рис. III.7, равен ІЦА^С), a tga = (С—1)(АаоС).
Необходимо отметить, что полимолекулярная адсорбция многих газов и паров в полной мере не соответствует теории БЭТ. Согласие с теорией тем лучше, чем больше константа КР по сравнению с константой KL, т. е. чем больше С или чистая теплота адсорбции. Этому способствует увеличение сродства адсорбата к адсорбенту и уменьшение когезионных сил в конденсате на поверхности.
На теории БЭТ основан стандартный метод измерения удельной поверхности адсорбентов, катализаторов, порошков и других материалов (метод БЭТ). По экспериментальным данным находят величину Лоо (см. рис. III.7), а затем по уравнению (III.19) рассчитывают удельную поверхность. В качестве адсорбатов используют инертные газы (азот, аргон, криптон и др.), которые проявляют слабое межмолекулярное взаимодействие на поверхности адсорбента, что находится в соответствии с исходными допущениями теории и обеспечивает достоверность получаемых результатов. Значения площади, занимаемой молекулой адсорбата в заполненном монослое ш0 принимают равной для азота 0,162 нм2, аргона—0,138 нм2, криптона— 0,195 нм2. Для увеличения адсорбции таких газов ее ведут при низких температурах, откуда и частое название метода БЭТ — метод низкотемпературной адсорбции. Уравнение изотермы БЭТ применяется с хорошим приближением в области относительных давлений 0,05<p/ps<0,3. При P/Ps<0,05 в получаемые результаты вносит искажения неоднородность поверхности (вывод уравнения БЭТ предполагает однородность поверхности), а при р/р^>0,3 сказывается взаимодействие между адсорбированными молекулами.
Названные ограничения показывают, что основные недостатки рассмотренных моделей адсорбции на однородных по-
Рис. III.7. Изотерма полимолекулярной адсорбции в координатах линейной формы уравнения БЭТ
^ і
Верхностях заключены в тех допуще — ^ ниях, которые заложены в основу предложенных моделей и теорий. В теории БЭТ, кроме того, обнаружива — _J_ ется противоречие между пренебреже — иием боковыми взаимодействиями между молекулами на поверхности и предположением о том, что константы адсорбции в верхних адсорбционных слоях равны константе конденсации пара. Как известно, константа конденсации определяется взаимодействием молекулы в среднем с двенадцатью ближайшими соседями, окружающими ее со всех сторон, а не только с двумя соседними по вертикали молекулами.
Предложено много модификаций уравнения теории БЭТ,, по, как правило, они описывают только частные варианты изотерм адсорбции. По-видимому, трудно исправить недостатки теории, не нарушив простоты, которая составляет ее серьезное достоинство.
 2 ноября, 2012
2 ноября, 2012  admin
admin 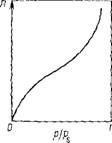
 Опубликовано в рубрике
Опубликовано в рубрике 