В адсорбционном уравнении Гиббса (11.70) влияние природы веществ на адсорбцию отражает производная да/да. Эта производная определяет и знак гиббсовской адсорбции. Таким образом, величина да/да может служить характеристикой поведения веществ при адсорбции. Чтобы исключить влияние концентрации на производную и придать этой величине вид характеристической постоянной, берут ее предельное значение при с-*-0; эту величину П. А. Ребиндер (1924 г.) назвал поверхностной активностью. Ее общее определение дается соотношением (Ю. Г. Фролов, 1987 г.)
£ = _ (да/да),,^ (И.75»
Которое справедливо как для неэлектролитов, так и для электролитов. При положительной адсорбции величина да/да имеет отрицательный знак [см. уравнение (11.70)]. Чтобы’знаки поверхностной активности и гиббсовской адсорбции совпадали, в уравнении (11.75) перед производной ставят знак минус.
Общее определение поверхностной активности при переходе к концентрациям (для разбавленных систем активность можно заменить на концентрацию) принимает соответствующие выражения:
Для неэлектролитов g = — >д<5/дс}с^о (II.76)
|
|
Для электролитов g± = — (<?o/dcv+)c±^o (11.77)
Поверхностная активность является важнейшей адсорбционной характеристикой веществ, определяющей многие их свойства и области применения. Единицами поверхностной активности неэлектролитов и электролитов являются Дж-м3′-2/моль или Н■ м3′-1/моль где v — стехиометрический коэффициент; для неэлектролитов — Дж-м/моль (v=l) или Н-м2/моль. Естественно, сравнивать поверхностные активности веществ можно только, если они выражены в одних и тех же единицах.
Уравнения (11.76) и (11.77) показывают, что чем сильнее уменьшается поверхностное натяжение с увеличением концентрации адсорбируемого вещества, тем больше поверхностная активность этого вещества. Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и рассчитанную на единицу гиббсовской адсорбции.
Поверхностную активность можно определить графически как отрицательное значение тангенса угла наклона касательной, проведенной к кривой o = f(c) для неэлектролита или к кривой a = f(c±-‘) для электролита в точке пересечения с осью ординат (см., например, рис. II.7, g = —tgao).
Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-ак — тивным. Для таких веществ
G > 0, да/дс < 0 (или да/дс"± < 0) и Г > 0
Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверх — постно-инактивными. Для них
G < 0, да/дс > 0 (или Da/Dcv± >0) и Г < 0
|
4* |
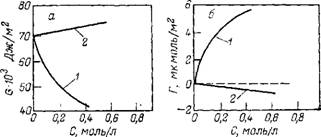
Отрицательная гиббсовская адсорбция Г<0 означает, что концентрация адсорбируемого вещества в объеме больше, чем в поверхностном слое. При увеличении концентрации поверх- ностно-инактивного вещества в объеме степень соответствующего роста его концентрации в поверхностном слое ниже. В результате с увеличением концентрации поверхностно-инактивного вещества в объеме растет отрицательная величина гиббсовской адсорбции. Эти зависимости наглядно иллюстрирует рис. II.8, из которого видны различия между поверхностно-активными (додециламин) и поверхностно-инактивными (сульфат натрия) веществами, растворенными в воде. Если же в качестве растворителя додециламина (а = 22,5 мДж/м2) взять гексан, поверхностное натяжение которого меньше (а=17,8 мДж/м2), то амин будет выступать уже как поверхностно-инактивное веще-
|
Рис. II.8. Зависимость поверхностного натяжения (а) и гиббсовской адсорбции (б) от концентрации водного раствора поверхностно-активного и инактивного вещества: / — додециламин; 2 — сульфат натрия |
Ство. Так как большинство органических веществ имеет поверхностное натяжение меньше, чем вода, то они по отношению к воде поверхностно-активны.
Термин «поверхностно-активные вещества» (ПАВ) обычно применяют к специфическим веществам, обладающим очень большой поверхностной активностью по отношению к воде, что является следствием их особого строения. Молекулы ПАВ имеют неполярную (углеводородную) часть и полярную, представленную функциональными группами —СООН, —МН2, —ОН, —О—, —S020H и др. Углеводородные радикалы выталкиваются из воды на поверхность, и их величина адсорбции всегда положительна ( Г>0). ПАВ типа обычных мыл (олеат натрия) в концентрации 10~3 моль/л понижают о воды при 298 К с 72,5 до 30 мДж/м2. Это значит, что в определенной толщине поверхностного слоя концентрация ПАВ в 3-Ю[2] раз (т. е. в десятки тысяч раз) превышает концентрацию ПАВ в объеме раствора.
Примером поверхностно-ииактивных веществ по отношению к воде являются неорганические соли, которые сильно гидрати — руются. Они взаимодействуют с водой сильнее, чем молекулы воды между собой. Вследствие этого они имеют отрицательную величину адсорбции (Г<0). При добавлении неорганических солей к воде поверхностное натяжение повышается, но в связи с тем, что адсорбция соли отрицательна, т. е. на поверхность предпочтительнее переходит растворитель (вода), поверхностное натяжение раствора с увеличением концентрации поверх — ностно-инактивных веществ растет медленно (см. рис. II.8).
Ется в конденсате пара, образующегося на его поверхности. При таком условии энергия Гиббса системы изменяется в соответствии с соотношением (11.69), для которого принято равенство Г = Л (большая избыточная адсорбция). Фундаментальное уравнение Гиббса в этом случае принимает вид (учитываются только параметры адсорбируемого газа—фазы 2):
— dSa = r-2d-n:. -— Ло= j IVAp2 (11.78)
Подставляя уравнение (11.78) в уравнение (11.69), получим:
AGS= Г2Лц2 — j ГггіАцг
Сравнение этого уравнения с применяемой в математике формулой интегрирования по частям[3] дает возможность записать:
Г*
Л(, — f Аі*!Гг (П.79)
‘о
Таким образом, зная зависимость величины гиббсовской адсорбции от химического потенциала адсорбата, можно рассчитать интегральное изменение энергии Гиббса в системе при адсорбции. Эта величина, взятая с обратным знаком, называется интегральной работой адсорбции:
Гаде = —AGs (11.80!
Дифференциальное изменение энергии Гиббса при адсорбции можно получить дифференцированием уравнения (11.79) по величине гиббсовской адсорбции Гг:
AGl/ = dAGs/dr2 = A(i2 (11.81!
Из этого уравнения следует, что дифференциальное изменение энергии Гиббса при адсорбции равно изменению химического потенциала адсорбата при переходе 1 моль его из стандартного состояния (жидкость, насыщенный пар) на поверхность адсорбента. Величина, равная дифференциальному изменению энергии Гиббса при адсорбции, взятая с обратным знаком, называется дифференциальной работой адсорбции, или адсорбционным потенциалом:
Е = — ц2 = ЯГ1п (Ps/P) (11.82!
Где р — давление пара (газа) адсорбата в адсорбционной системе; Ps — Давление насыщенного пара над жидким адсорбатом. Очевидно, пары в этом случае принимаются за идеальные.
Так как адсорбция увеличивается с ростом давления (концентрации) вещества, то из уравнения (11.82) следует, что дифференциальная работа адсорбции, уменьшаясь с увеличением давления (концентрации) адсорбата, уменьшается и с ростом величины адсорбции.
Дифференциальное изменение энтропии можно получить, дифференцируя AGd по температуре с учетом (11.82):
|
(5Д(.І.2 ~ЪТ |
|
D№d ДТ |
|
Д In (p/ps)" |
|
— R In — f — — RT |
|
BSd = — |
|
ДТ |
|
Ps |
|
Г2 |
|
Га |
Или
|
D In ps DT |
|
RT |
|
(11.83) |
|
Г2 |
Р _____ / <Э In р
ДТ
В последнем слагаемом можно записать прямую производную, так как Ps не зависит от Г2.
Дифференциальное изменение энтальпии легко получить, подставив в уравнение A#d = AGd + TASa соответствующие выражения из уравнений (11.82) и (11.83):
|
D in (Р/Р,)‘ Д T |
|
MJd = RTn |
|
— RT In — — RT* Ps |
|
Ps |
|
Ra |
|
Д In (p/ps) |
|
RT2 |
|
A Hd— |
|
Д T |
|
R2 D in ps DT |
|
<3 In p DT |
|
(11.84) |
|
■RT2 |
|
BHd> |
|
RT2 |
|
Или |
Из уравнений (11.83) и (11.84) видно, что для расчета дифференциальных изменений энтропии и энтальпии необходимо знать зависимость давления пара от температуры при постоянной величине адсорбции Г (определение изостер). По этим зависимостям можно получить необходимые значения температурных коэффициентов для давления пара при данных заполнениях поверхности адсорбента — величинах адсорбции. Первый член правой части уравнения (11.84) выражает дифференциальную теплоту адсорбции:
(11.85)
Второй член отвечает теплоте объемной конденсации пара:
Dlaps
L — — RT2 dP— (11.86)
Изменение энтальпии адсорбции получило название чистой дифференциальной теплоты адсорбции-.
Xa=qd — L (11.87)
|
A=const |
|
<ti |
M
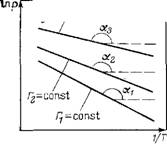
Для определения дифференциальной теплоты адсорбции строят график в координатах In р—1 /Т (рис. IL9), что соответствует интегральной форме уравнения (11.85) для дифференциальной теплоты адсорбции при условии независимости <7,г от Т:
+const (11.88)
Дифференциальная теплота адсорбции определяется по тангенсу угла наклона прямой (tga = qd/R). Построение изостер при разных заполнениях поверхности адсорбента позволяет проследить изменение дифференциальной теплоты адсорбции, которую часто называют изостерической. По мере заполнения поверхностного слоя абсолютное значение изостерической теплоты адсорбции уменьшается. Из рис. П.9 видно (tga<0), что теплота адсорбции паров и газов отрицательна (энтальпия уменьшается), т. е. теплота выделяется из системы. Как следует из соотношения (II.85), она измеряется в единицах теплоты, приходящейся на единицу количества адсорбата (Дж/моль).
Интегральную теплоту адсорбции можно получить интегрированием дифференциальной теплоты адсорбции и чистой дифференциальной теплоты адсорбции:
Г2 г2
Qa = ( qjdr2 и Qra == С vr2 (11.89)
‘о о
Эти величины определяют теплоту адсорбции до данного заполнения поверхности и в соответствии с уравнением (11.89) измеряются в единицах теплоты, приходящейся на единицу Площади поверхности (или массы) адсорбента.
На рис. 11.10 представлены зависимости интегральных и дифференциальных теплот адсорбции от величины адсорбции, которые показывают, что абсолютные значения дифференциальных теплот обычно уменьшаются по мере увеличения адсорбции (степени заполнения). Это уменьшение сильнее проявляется на энергетически неоднородных поверхностях, которые характерны для большинства реальных адсорбентов, и объясняется тем, что в первый момент молекулы адсорбата взаимодействуют с обладающими большим сродством центрами адсорбции и теплота адсорбции максимальна. По мере заполнения поверхности во взаимодействие вступают адсорбционные центры с меньшим сродством к данному адсорбату, и соответственно уменьшается теплота адсорбции. Она уменьшается и по мере увеличения толщины слоя адсорбата на адсорбенте.
Интегральные теплоты определяются площадью под кривыми, описывающими дифференциальную теплоту.
Форма кривых теплот адсорбции на реальных адсорбентах значительно сложнее. Усложнение обсуждаемых зависимостей часто связано с тем, что при малых степенях заполнения поверхности вклад теплоты конденсации небольшой и изменение энтальпии определяется в основном чистой теплотой адсорбции. По мере же заполнения вклад теплоты конденсации нарастает. Поэтому на кривой могут наблюдаться и минимумы; возможны и более сложные зависимости.
 2 ноября, 2012
2 ноября, 2012  admin
admin 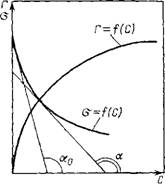
 Опубликовано в рубрике
Опубликовано в рубрике 