Отклонения от закона Генри, выражаемые изменениями коэффициентов активности в фазах, обычно не позволяют описать и прогнозировать ход изотерм с увеличением концентрации (давления) адсорбата. Чтобы получить теоретическую изотерму адсорбции, описывающую более широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей.
Изменения коэффициентов активности (или фугитивности) с концентрацией (давлением) в объеме часто не являются значительными и отклонения от закона Генри в основном обусловлены существенной зависимостью коэффициентов активности адсорбата от его концентрации в поверхностном слое, (т. е. от величины адсорбции или степени заполнения поверхности). Оказалось, что большую долю отклонений коэффициента активности адсорбата в поверхностном слое от единицы можно учесть, используя представление об адсорбции как о квазихимической реакции между адсорбатом и адсорбционными центрами поверхности адсорбента, В этом заключается основная идея адсорбционной теории Ленгмюра, которая явилась фундаментальным вкладом в учение об адсорбции. Эта теория позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение является основным в теории Ленгмюра и уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом.
Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
А+В =Fs АВ
Где А — адсорбционные центры поверхности; В — распределяемое вещество;. ЛВ — комплекс, образующийся на поверхности.
По мере увеличения концентрации (давления) вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия (без учета коэффициентов активности реагирующих веществ) равна
К = САВ/1СА-Св> (111,12)
В этом соотношении
СдВ=і4 и сл=і40=і4»—А (III.13)
Где А—величина адсорбции; Л»—емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единицу площади поверхности нли на единицу массы адсорбента; А0 — число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности или на единицу массы адсорбента.
Подставляя уравнение (III.13) в уравнение (III.12), получим:
А
(А., —А) с или А — АхКс — АКс
Окончательно имеем:
Выражение (III.14) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:
(III..5)
Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра (К и КР) характеризует энергию взаимодействия адсорбата с адсорбентом (химическое сродство AG0). Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия (ДС° = —RT In К).
Адсорбционное уравнение Ленгмюра часто представляют относительно степени заполнения поверхности — отношения величины адсорбции А к емкости монослоя
А Кс с
= 1 + = (НІ-Ш)
Где К’=1/К.
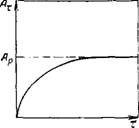
Типичная изотерма адсорбции Ленгмюра показана на рис. III.4. Важны экстраполяционные следствия из соотношений (III.14) — (III.16). При малых концентрациях или давлениях, когда с—>-0, получаем:
А = А^Кс и в = Кс (111.17)
Выражения (111.17) соответствуют закону Генри (АосК= Яг)- величина адсорбции линейно растет с увеличением концентрации. Таким образом, уравнение Ленгмюра является более общим соотношением, включающим и уравнение Генри. При больших концентрациях и давлениях, когда Кс^> 1 и KPp^>L уравнения (III.14) — (111.16) переходят в соотношения
Л=Л„ и 0 = 1 (1П.18>
Її И
Рис. III.4. Изотерма адсорбции Ленгмюра
Рис. II 1.5. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра
Соотношения (III.18) отвечают состоянию насыщения, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальное определение Ах позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):
(111.19)
Где Ах — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; Vл — число Авогадро; w0 — площадь, занимаемая одной молекулой адсорбата.
Интересна зависимость доли свободной поверхности адсорбента от концентрации адсорбата при больших степенях заполнения поверхности:
|
0,.= І — Є: |
|
(III.20) |
Кс I
I
I 4- Кс ~ I Кс
При больших степенях заполнения Кс1 и
В0= I/< А’П
Из уравнения (III.20) видно, что при больших степенях заполнения доля свободной поверхности обратно пропорциональна концентрации адсорбата в объеме.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме [числитель (III.14) переносят в знаменатель, а знаменатель — в числитель]:
II II
Умножив на ААЖ, получим
A=A„ — (I/К)0
Или
|
|
С/А = 1/(А„Ю+с/А,
Такие линейные зависимости позволяют графически определить оба постоянных параметра (Л«> и А’) адсорбционной изотермы. На рис. II 1.5 представлена типичная изотерма адсорбции в координатах уравнения (III.23). Экстраполяция за^. нисимости до оси ординат дает отрезок, равный ІЦА^К), а і апr ettc угла наклона прямой а равен 1 /Ах.
При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров А0 является общей для равновесной многокомпонентной системы. Константы равновесия адсорбции для каждого газа выразятся так:
К< ~ ~Іл; н т-д-
Откуда величина адсорбции каждого компонента будет равна
А,~А0КіРі А2^А0К2р2, Аг=АоКіРі и т. д. Степень заполнения для г-го компонента составит:
Аі Аі АоКіРі
"і ! ‘ « r=s я
Ап — i — VAt А0 І У.4,Д ,•/;,■ і і
Окончательно получим
————- (Ш.24)
І : v Кт
І
Из уравнения (II 1.24) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия.
Все рассмотренные до сих пор уравнения справедливы для мопомолекулярной адсорбции, протекающей на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности твердых тел, как правило, не обладают такими свойствами. Для приближения к реальным условиям целесообразно рассмотрение возможных распределений адсорбционных центров поверхности адсорбента по энергиям. Приняв линейное распределение адсорбционных центров по энергиям (теплота адсорбции линейно зависит от заполнения поверхности 0), М. И. Темкин, используя уравнение Ленгмюра, получил следующее уравнение для средних степеней заполнения адсорбента:
Где «—постоянная, характеризующая линейное распределение: К о кои — сі. інта в уравнении Ленгмюра. отвечающая максимальной теплоте адсорбции.
Уравнение (III.25) обычно называется логарифмической изотермой адсорбции.
Если принять экспоненциальное распределение неоднород — постей поверхности (теплота адсорбции представляет собой ло — I арифмическую функцию заполнения поверхности 0), то, как показал Я. Б. Зельдович, в области средних заполнений получается ранее найденное эмпирически уравнение Фрейндлиха:
А-=Кр* " (111.26)
Где Кип — постоянные.
Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных, в том числе в инженерных расчетах. Чаще всего оно применяется в логарифмической форме
In 4= In АЧ 1Дг 1пр (111.27)
Позволяющей построить линейную зависимость ІП/4—Чпр и графически определить оба постоянных параметра /(ил.
 2 ноября, 2012
2 ноября, 2012  admin
admin 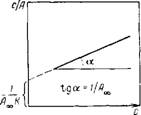
 Опубликовано в рубрике
Опубликовано в рубрике 