Укрывистость, интенсивность, а также такие колористические показатели пигментов, как доминирующая длина волны и чистота цвета, при неизменном химическом составе и кристаллической модификации зависят прежде всего от их дисперсности.
Укрывистость. Рассеяние света частицами пигмента обусловлено разностью показателей преломления пигмента и среды, в которой он диспергирован. В случае крупных частиц, т. е. частиц, размеры которых значительно превышают длины волн видимого света, рассеяние сводится к многократному зеркальному отражению светового потока поверхностями частиц. Если же частицы соизмеримы с длинами волн света, его рассеяние имеет другой механизм.
При прохождении света через однородную среду все ча«. ищы подвергаются поляризации, зависящей от частоты электромагнитных колебаний. В результате поляризации образуются диполи с переменным электрическим моментом, которые снова излучают свет, т. е. сами являются источником электромагнитных колебаний. Согласно принципу Гюйгенса, — свет, излучаемый диполями, распространяется в том же направлении, что и падающий поток, с интенсивностью подающего потока. Если в системе присутствуют частицы, поляризуемость и показатель преломления которых отличаются от поляризуемости и показателя преломления среды, то и диполи, получающиеся в результате поляризации, имеют другие дипольные моменты. Излучение этих диполей не равно излучению остальной среды. Такое некомпенсированное излучение наблюдается в виде рассеянного света, интенсивность которого 18 для сферических, неиоглощающих свет частиц определяется уравнением Рэлея:
|
|
(2.35)
Где а — угол между направлениями потоков рассеянного и падающего света; Ь — расстояние до частицы; X — длина волны падающего света; и, и п0 — показатели преломления частицы и среды; V — объем частицы; /0 — интенсивность падающего света.
Уравнение Рэлея справедливо только для непоглощающих свет частиц, размеры которых не больше 0,07 Л.
![]() Теория рассеяния света поглощающими свет частицами разработана Ми. Уравнения для расчета интенсивности рассеянного света 1$ по теории Ми имеет следующий вид:
Теория рассеяния света поглощающими свет частицами разработана Ми. Уравнения для расчета интенсивности рассеянного света 1$ по теории Ми имеет следующий вид:
(2.36)
Где а = 2эт*?/Л; £? — диаметр частицы; т — комплексный показатель преломления;
Т=п1[1 — Ж (Л) ]; К (К) — коэффициент поглощения.
Таким образом, по теории Ми интенсивность рассеянного света для данной длины волны и данного размера частиц определяется не только соотношением показателей преломления частиц и среды, но и коэффициентом поглощения.
Для частиц с размерами менее 0,07Л, когда действует закон Рэлея, светорассеяние прямо пропорционально шестой степени размера частиц.
Согласно теории Ми, зависимость светорассеяния от размеров частиц выражается кривой с максимумом, который наблюдается для частиц
Ш 500 600 700
|
Диаметр частиц |
![]() Х, нм
Х, нм
Рис. 2.4. Общая зависимость интенсивности рассеянного света от размера частиц дисперсной фазы.
Рис. 2.5. Спектральная зависимость функции Гуревича — Кубелки — Мунка для желтого свинцового крона с различным средним размером частиц, разбеленного цинковыми белилами в соотношении 3:1.
С размерами 0,25Х—0,3.3л. На рис. 2.4 приведена общая зависимость интенсивности рассеянного света от размера частиц дисперсной фазы.
Ограниченность теории Ми для реальных пигментированных систем обусловливается анизодиаметричностью частиц, характерной для большинства пигментов, и чрезвычайно высоким содержанием дисперсной фазы в системе, при котором несколько частиц могут проявлять себя оптически как одна. В работе [114] рассмотрено влияние ОКП на укры — вистость на примере диоксида титана. Установлено, что укрывистость остается постоянной только до определенного значения ОКП.
Пигмент в лакокрасочном материале полидисперсен и характеризуется определенной функцией распределения частиц по размерам. Бо — быренко [115] получена следующая зависимость коэффициента рассеяния покрытия от наивероятнейшего радиуса частиц пигмента:
|
Где <р — объемное содержание пигмента (ОКП); гн — радиус частиц пигмента, соответствующий максимуму дифференциальной массовой функции распределения размеров частиц, т. е. наивероятнейший радиус; х — доля световой энергии, рассеянной частицами пигмента в направлении „назад”, х = 0,5(1 -«,/«„); к — константа, характеризующая оптические свойства частиц пигмента и среды и зависящая от показателей преломления пигмента и, и среды п0 и длины волны света. |
|
|
(2.38)
Наивероятнейший радиус частиц пигмента, соответствующий максимальному значению коэффициента рассеяния, а следовательно, и максимальной укрывистости, равен [115]:
Из уравнения (2.39) следует, что оптимальный наивероятнейший радиус частиц пигмента зависит от их показателя преломления. Максимальная укрывистость для пигментов, имеющих больший показатель преломления, соответствует меньшим размерам, частиц:
TOC o "1-5" h z Г °пт п1
Диоксид титана, рутил 0,08—0,10 2,9
Диоксид титана, анатаз 0,10-0,13 2,3
Оксид цинка 0,17—0,20 2,0
Для монодисперсных пигментов Бобыренко приводит следующее уравнение [115]:
Гп = 0,725 Л/-п(п1-п0) (2.40)
Из сравнения уравнений (2.40) и (2.39) следует, что оптимальный наивероятнейший размер частиц полидисперсного пигмента в 1,8 раза меньше, чем для монодисперсного. Уравнение (2.39) выведено для полидисперсности, характеризуемой константой полидисперсности ()т = 1,04-5- •5-1,06, наиболее характерной для пигментов.
Интенсивность пигментов также основана на оптических явлениях, характерных для коллоидных систем, и при прочих равных условиях зависит от дисперсности пигмента: с ростом дисперсности пигмента интенсивность повышается. По изменению интенсивности пигментов в процессе диспергирования, как указывалось в разделе 2.2,можно судить об изменении размера частиц. Для ряда пигментов (красного и желтого же — лезоокисного, кадмиевых пигментов) показано, что нарастание интенсивности в процессе диспергирования описывается гиперболической функцией.
На рис. 2.5 приведены спектральные зависимости функции Гуревича — Кубелки — Мунка для желтого свинцового крона. В минимуме абсорбции света значение функции К(X) /5 (X) практически не зависит от среднего размера частиц пигмента, в то время как в максимуме абсорбции (для Х = 450 нм) уменьшение среднего размера частиц в 6 раз вызывает более чем трехкратное возрастание значения функции К (X) /5 (X).
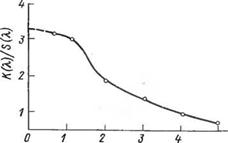
Зависимость функции Гуревича — Кубелки — Мунка от среднего размера частиц 5 в максимуме абсорбции света (рис. 2.6) выражается уравнением:
КШМл) = [я(г)/5(Л)]о е~ьаС (2.41)
Где <1 — диаметр частиц; [К ()/ £(Л.)] 0 — предельное значение функции Гуревича — Кубелки — Мунка; Ь и с — коэффициенты.
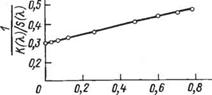
Значение [К(X) /£ (X) ]о может быть определено из зависимости обратного значения функции К(X) /5 (X) от т~1 (где т — продолжительность диспергирования) путем экстраполяции к бесконечно большой
|
Рис. 2.6. Зависимость функции Гуре- Продолжительности диспергиро- 5 ми, [Я (Х)/5(Х) ]0 =3,3. Для Й, мкм вычисления коэффициентов Ь И с экспериментальные данные обрабатывали по методу наименьших Я(Л)/5(А) |
|
(2.42) |
|
:1|Г! 0,434 Ь+ с1дс( |
|
ІГ |
|
[й(Л)/5(д)]0 |
|
Рис. 2.7. Зависимость обратного значения функции Гуревича — Кубелки — Мунка от обратного значения продолжительности диспергирования желтого свинцового крона. — ,, ф^(Х)/£(Х)] *(Х)/5ЧХ) Гис. 2.8. Зависимость — |
|
Для желтого свинцового |
|
[^(Х)/5(Л)]о |
|
Йт |
|
Крона. |
|
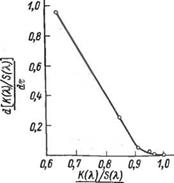
Получены значения: Ь — 0,2 и с = 1,35. Интенсивность пигмента повышается с ростом дисперсности, однако при приближении к определенцому значению К(X) /5 (X) это повышение резко замедляется и дальнейшее диспергирование становится уже нецелесообразным. Такое значение К(X) /£ (X) следует считать оптимальным. /С(Х)/Я(Х) |
|
При достижении значения [ЛГ(Х)/5]о Вание практически уже не влияет на интенсивность пигмента. Оптимальный размер частиц, исходя из этого, может быть вычислен по уравнению: |
|
0,9 (см. рис. 28), диспергиро- |
 |
|
 |
|
|
|
 |
Для желтого крона, согласно уравнению (2.43), <2ОПТ=0,67 мкм.
Значение [/Г (К) /5 (X) ] 0 может быть, рассчитано, однако с меньшей точностью, из выражения:
, 1^[Я(Л)А(Л)]2-{1д[щг)А(Л)13}2
[к(л)/5(*)],+[я(*)/л-(/У]2-21£ [й(/)/Л’Ы]э ‘ ■
Где и [А'()/5()]2 — значения функции Гуревича — Кубелки —
Мунка для выбранных <11 и(/2; [/ГО)/5()]3 — значение функции Гуревича — Кубелки — Мунка для <1г — /ё1аг.
Для желтого крона по уравнению (2.44) получено значение [/Г(Х)/5(Х)]0=3,5.
Аналогичные расчеты были проведены по имеющимся в литературе экспериментальным и рассчитанным по теории Ми данным для р-фтало — цианина меди. Значение [/<*(X) /5 (X) ] 0 было рассчитано по уравнению (2.44). Оптимальное значение размера частиц этого пигмента <2опт, вычисленное по уравнению (2.43), оказалось равным 0,087 мкм, что близко к приведенному в работе [116] значению 0,08 мкм.
Как показали наши исследования и исследования Хаузера, Германа и Хонигмана [116], несмотря на то что современное диспергирующее оборудование позволяет проводить диспергирование до первичных кристаллов, на практике интенсивность перестает расти при достижении определенной дисперсности. Это, по всей вероятности, объясняется тем, что при введении разбеливающего пигмента, имеющего меньшую дисперсность, чем цветной пигмент, частицы цветного пигмента, заключенные между частицами белого пигмента, оптически ведут себя как одна, и дальнейшее диспергирование не вызывает повышения интенсивности.
|
&,мкм |
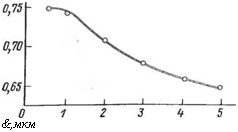 Увеличение дисперсности пигментов, приводящее к росту укрывисто — сти, интенсивности и чистоты цвета (рис. 2.9), изменяет и цветовой тон пигмента. Цвет вещества зависит от положения полосы поглощения в видимой части спектра, однако на оттенок пигмента в большой степени влияет форма и размер частиц, так как спектр отражения определяется не только спектром поглощения, но и характером рассеяния света. Так, увеличение частиц свинцового оранжевого и красного свинцово-молиб — датного кронов приводит к смещению максимума Отражательной способности пигмента в длинноволновую область, т. е. к усилению красного оттенка. Рост кристаллов при синтезе желтого
Увеличение дисперсности пигментов, приводящее к росту укрывисто — сти, интенсивности и чистоты цвета (рис. 2.9), изменяет и цветовой тон пигмента. Цвет вещества зависит от положения полосы поглощения в видимой части спектра, однако на оттенок пигмента в большой степени влияет форма и размер частиц, так как спектр отражения определяется не только спектром поглощения, но и характером рассеяния света. Так, увеличение частиц свинцового оранжевого и красного свинцово-молиб — датного кронов приводит к смещению максимума Отражательной способности пигмента в длинноволновую область, т. е. к усилению красного оттенка. Рост кристаллов при синтезе желтого
Рис. 2.9. Зависимость чистоты цвета от среднего размера частиц желтого свинцового крона.
Железоокисного пигмента ведет к сильному потемнению продукта. Варьируя размеры частиц красного железоокисного пигмента, можно получить целую гамму оттенков. Уменьшение среднего размера частиц желтого свинцового крона с 4,8 до 0,8 мкм смещает доминирующую длину волны с 583 нм до 577 нм, т. е. смещает цвет в сторону зеленого на диаграмме цветности. Общим правилом является смещение максимума отражения при диспергировании пигментов в коротковолновую область спектра.
Красные и желтые пигменты при уменьшении дисперсности приобретают голубоватый или зеленоватый оттенок; грубодисперсные зеленые пигменты имеют желтоватый, а высокодисперсные — голубоватый оттенок; мелкие частицы синих пигментов имеют зеленоватый, а крупные — красноватый оттенок. Увеличение дисперсности белых пигментов повышает их белизну за счет-уменьшения поглощения в низковолновой части спектра, что особенно характерно для диоксида титана рутильной модификации.
 13 сентября, 2013
13 сентября, 2013  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике 