Большинство авторов обобщило результаты своих исследований в виде критериальных уравнений, которые можно вывести, используя метод анализа размерностей. Для этого необходимо установить, какие параметры имеют существенное влияние на величину коэффициента теплоотдачи и, таким образом, войдут в искомое уравнение. В соответствии с проведенными при экспериментальных исследованиях наблюдениями, это должны быть следующие параметры:
A = f(n, d, у, Л, К с, D) (V-18)
Размерности отдельных величин в уравнении (V-18):
-№]•■ ‘-м
Напомним, что
Можно представить функцию (V-18) в виде степенного произведения:
А = C^d^fX^D1 (V-19)
Используя размерности величин, получим:
Чтобы уравнение (V-19) было однородным относительно размерностей, показатели степеней должны отвечать следующим зависимостям: для [кг]
1 = e+f+S
Для [м]
Для [с] для [К]
Получаются четыре уравнения с семью неизвестными. СледоваТельно, приняв, что три из этих показателей степени известны, Например е, h, i, имеем:
А — е
B = 2e — i — 1 f=h-e g = -h
После подстановки этих показателей степени в уравнение (V-19), оно примет вид:
А СхпЧ^-^цЪ-еЫ-ЪсЬо1 (V-20)
|
АР Т~ |
После преобразования до безразмерных комплексов, получим:
Ч^ут^т1
Уравнение (V-21) можно написать в другой форме, если использовать критерии подобия: критерий Нуссельта
«Я —=Nu
Критерий Рейнольдса для процессов перемешивания
|
Ц сц Т D |
|
Рг |
Nd*y
= Re
Критерий Прандтля
Кроме того, выражение
Является инвариантом геометрического подобия. Тогда можно записать:
/ Л у+1
(-г) Cl = f(*D)Cl = C
Окончательно получим:
Nu = CReAPrB (V-22)
При использовании подстановки (D/d)l+1Cl = С было принято Дополнительное обозначение: (D/d)t+1 = / (ID), так как разные авторы не всегда обобщали влияние отдельных геометрических параметров в виде поправок, представляющих показательную функцию. Иногда это была функция другого типа, например тригонометрическая и т. д. Следует отметить, что в уравнении (V-22) может
быть использовано иное определение критерия Нуссельта. Это особенно касается теплоотдачи в случае установки змеевика, потому что разные авторы принимают в качестве линейного размера в критерии Нуссельта то наружный диаметр трубы змеевика dw, то диаметр витка змеевика Dw, то внутренний диаметр сосуда D аппарата с мешалкой.
Уравнение (V-22) справедливо для постоянных геометрических параметров аппарата с мешалкой или же для семейства геометрически подобных аппаратов, инварианты геометрического подобия которых постоянны. Для описания теплоотдачи в различных аппаратах с мешалкой, которые не отвечают этим условиям, нужно применять следующие уравнения:
Nu = C1ReAPrB/(i1) (V-23)
Nu = С2 ReAPrB/ (/ (i2) (V-24)
Где f (£х), / (i2), … — поправки, учитывающие влияние геометрических параметров аппарата с мешалкой на теплоотдачу.
Инварианты геометрического подобия i2, . . ., появляющиеся в этих поправках, могут относиться или к диаметру мешалки, например D/d, b/d, или к диаметру сосуда, например d/D,H/D, и т. д.
Уравнения (V-23) й (V-24) неудобно применять, так как постоянные Сг и С2 принимают разные значения в зависимости от числа введенных инвариантов. Эти уравнения можно преобразовать, пользуясь понятием типового аппарата с мешалкой, для которого обязательны инварианты £01 = (ijd)0, £о3 = (i^/d)0, что дает поправки / (ioi). / (НчУ-
Nuo = C1ReAPrB/(ioi) (V-25)
Nu0 =С2 ReAPrB/ (ioi) / (Г02) (V-26)
|
(V-27) (V-28) |
Из уравнений (V-23), (V-25) и (V-24), (V-26) можно получить:
M^CReAPrB4r~
F(i 01)
Nu = C ReW • Ш—
/(»01) /(»02) Причем
С If {Ioi) = C2F (ioi) / (’02) = • • • = С (V-29)
Значение постоянной С не зависит от числа введенных поправок / (г). Уравнения (V-27) и (V-28) можно представить в виде:
Nu = С КеАРг®гМ>2- • • (V-30)
Где
Поправки я}?! и i|)2, выражающие влияние геометрических параметров аппарата с мешалкой на теплоотдачу, имеют то преимуще
Ство, что для типовых аппаратов они принимают значения ярХ = 1, <фа = 1, • • • Для этого случая уравнение (V-30) примет вид:
Nu = CReAPrB (V-31)
Показатели степени А ж В, постоянная С, а также поправки г^, <ф2, . • • должны определяться экспериментально. Их значения были Найдены многими авторами.
В литературе встречаются также зависимости, которые содержат в себе поправки, выражающие одновременное влияние двух или большего числа инвариантов геометрического подобия в виде одной поправки/ I2)J(I1, I2, i3) и т. д. Либоя})1)2, г|эь2|8 и т. д. [56, 59, 60].
Для расчета коэффициентов теплоотдачи с помощью уравнения (V-31), как правило, используются средние значения физических параметров жидкости, находящейся в аппарате.
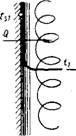
В уравнении (V-31) влияние направления теплообмена (нагревание, охлаждение) отражается на значении постоянной С. Она выше для нагревания, чем для охлаждения. Это является следствием того, что физические параметры ядра жидкости отличаются от физических параметров ее пристенного слоя, который имеет решающее значение в общем сопротивлении теплоотдаче. Например, если в двух разбираемых процессах температура ядра жидкости одинакова Tx = T2 = T (рис. V-2) и одинаковы остальные параметры, т. е. Rex = Re2, Prx = Рг2, то уравнение (V-31) с постоянной С = = const для обоих процессов дало бы одинаковый результат. Это будет противоречить эксперименту, поскольку Tsl^> T и Ts2 <; T, И, следовательно, пристенные слои в обоих процессах будут иметь разную вязкость, а значит и различную толщину. Более выгодные условия теплообмена будут при нагревании (ниже вязкость). В этом случае коэффициент а будет выше, что учитывается повышением значения постоянной С. Кроме того, постоянная С должна меняться с изменением температуры стенки Ts.
Чтобы избежать этих трудностей, Сидер и Тэте [73] предложили ввести в уравнение (V-31) поправку, учитывающую изменение физических параметров жидкости в пристенном слое с изменением температуры Ts. Поскольку только вязкость жидкости меняется с изменением температуры, эта поправка имеет вид:
|
|
|
|
|
Рис. V-2. Влияние поправки (r|/ris)B: Ti = t2 — температура ядра жидкости; Tsv ‘S2— температура стенки (индекс «1» относится к параметрам процесса нагревания, индекс «2» — к параметрам процесса охлаждения); Re, = Re2; Pr, = Pr2; LSl > W a> > |
Где г) и r|s — вязкости жидкости при температуре T и температуре стенки Ts соответственно.
В литературе можно встретить поправку, представляющую собой отношение критериев Прандтля (Pr/Prs)E. В случае неньютоновских жидкостей, подчиняющихся степенному реологическому закону, используется поправка (K/ks)E, где к и ks — постоянные Оствальда при температурах t и ts.
После подстановки поправки Vе уравнение (V-31) принимает вид:
Nu=CReAPiBVE (V-32)
Оно может быть использовано как для процесса нагревания, так и охлаждения. Таким образом, уравнение (V-32) наиболее универсально.
В табл. V-1—V-8 представлены результаты экспериментальных исследований процесса теплоотдачи, полученные различными авторами для разных типов аппаратов с мешалками и обобщенные в виде уравнения (V-32). Кроме того, в этих таблицах приводятся некоторые сведения о размерах аппаратуры и параметрах проводимого процесса, а также даны значения показателей степени А, В, Е и постоянной С уравнения (V-32).
Значение показателя степени А при критерии Рейнольдса изменяется в довольно широких пределах (А = 0,4-^-0,92). В литературе можно встретить утверждения, что этот показатель степени зависит от многих факторов, таких как тип мешалки, состояние поверхности теплообмена, направление движения тепла (нагревание, охлаждение) и т. д. В настоящее время трудно установить, какие из этих утверждений правильны. Одно верно, что показатели степени А зависят от режима течения жидкости (ламинарный, переходный, турбулентный), а следовательно, и от диапазона значений критерия Рейнольдса. Для турбулентного течения чаще всего принимается А = 2/3.
Показатель степени В при критерии Прандтля зависит прежде всего от свойств жидкости (вязкости) и направления движения тепла (нагревания, охлаждения), но некоторые авторы утверждают, что В зависит также от геометрических параметров системы. Чаще всего приводится В — х! ъ или значения, близкие к 73.
Значение показателя степени Е при симплексе вязкости V = — г)/тъ, найденное Сидером и Тэте [73] на основе исследований теплообмена во время течения жидкости по нагревающей или охлаждающей трубе и для диапазона V = 0,0042-^-9,75, равно 0,14. Большинство исследователей приводят такое же значение Е. Олдшу и Греттон [65 ] высказали мнение, что показатель степени Е является функцией значения самого симплекса V. Затем Хрубы [40 ] обосновал эту гипотезу. Хэкл и Виттмер [32 ] на основе собственных экспериментальных исследований, установили следующее.
1. Для диапазона V = V1ls >0,0125 значение показателя степени Е постоянно и равно 0,14.
2. Для диапазона V = 0,001-^-0,0125 величина показателя степени описывается зависимостью:
+ы) <v-33)
Для жидкостей малых вязкостей (близких к вязкости воды) значение показателя степени Е = 0,14.
Далее рассмотрим уравнения, по которым рассчитывается процесс теплоотдачи для различных типов мешалок.
 30 ноября, 2012
30 ноября, 2012  admin
admin 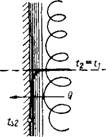
 Опубликовано в рубрике
Опубликовано в рубрике 