Два физических явления подобны, если подобны все параметры, их характеризующие. Это означает, что в соответствующих точках обеих систем и в соответствующие моменты времени параметр ф, относящийся к первому явлению, пропорционален тому же параметру другого явления ф’, причем ф’/ф = Сф является константой подобия для данного параметра.
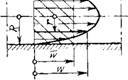
Это легко объяснить на примере подобия распределения скоростей жидкости в трубе при ламинарном потоке (рис. 1-3). Распределение скоростей для такого течения определяется уравнениями:
—W С[3] -(ж)*]
Из приведенных уравнений следует для соответствующих друг другу точек (r/R)x= (r‘/R‘)(r/R)2 = (r‘/R‘)2 и т. д. Отношение скоростей жидкости будет идентичным:
= (1-8)
W w
Где Cw — константа подобия полей скоростей.
Рассматриваемое явление может быть описано несколькими величинами, и для каждой из них константа подобия С может иметь другое значение. Следовательно, можно получить подобие плотностей, полей температур, скоростей и т. д.
|
У |
|
■■Сг |
Г Т
Для существования подобия более сложных явлений достаточно, чтобы константы подобия С были связаны определенной для этого
|
|
Рис. 1-3. Подобие полей скоростей при ламинарном течении жидкости в трубах.
Явления зависимостью. Если, например, насосный эффект мешалки определяется формулой
V*p = 0,4nd* (1-9)
Для другой геометрически подобной мешалки
(V*p)’ = 0An'(d’)3
|
CnCd |
То, принимая (У*)’ = CvV*P, п’ = Спп и D‘ = Cdd, получим:
(МО)
|
17 |
После деления уравнения (1-Ю) на уравнение (1-9), имеем:
1 (1-11)
|
К |
|
(1-12) |
Полученное выражение носит название индикатора подобия. Уравнение (1-11) можно преобразовать, подставив определения констант подобия:
(VpY
Л — idem
П‘ (d’)3
Слово idem означает, что выражение я, представляющее безразмерную группу параметров, должно быть идентичным для обеих мешалок. Такие безразмерные группы параметров носят название модулей подобия, коэффициентов подобия или критериев подобия
Подобие явлений требует, таким образом, идентичности соответствующих критериев подобия. Эти критерии обычно называются именами ученых, имеющих заслуги в данной области науки (например, критерии Рейнольдса Re, Фруда Fr, Вебера We и т. д.). Критерии имеют также определенный физический смысл и значение.
 29 ноября, 2012
29 ноября, 2012  admin
admin 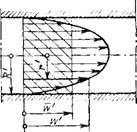
 Опубликовано в рубрике
Опубликовано в рубрике 