Лако-красочные материалы — производство

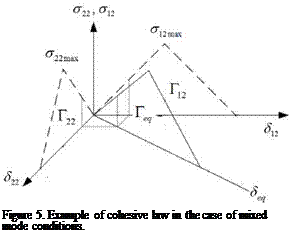
With the aim to extend the model to mixed-mode I/II conditions, a mixed mode cohesive law has to be defined. This is done according to the scheme shown in Figure 5 from the knowledge of the pure mode I and pure mode II cohesive laws (the index 22, refers to opening or mode I direction, index 12 refers to sliding or mode II direction)

First of all the mixed mode equivalent opening has to be defined. This is done using the relationship

In case of pure mode I this equation yields the value of S22 in case of positive d22, while it gives 0 in case of negative d22. This is done since it is supposed that compression stresses do not lead to the damage of the adhesive layer. Of course S22 assumes only positive values if crack surface interpetration is properly prevented in the model. In the present model, interpenetration is prevented by restoring element stiffness if values of S22 < 0 are detected.

Moreover, the mixed mode cohesive law is defined in terms of the initial stiffness (Кщ0), damage initiation equivalent opening (deq,0) and critical equivalent opening (SeqC). The equivalent initial stiffness is obtained by equating the equivalent strain energy (UEq) to the total strain energy (UTOt), which in turn is equal to the sum of the strain energy in mode I (U22) and in mode II (U12)

Ueq = Utot = U22 + U12 = 1 • Seq[1] • Г = 1 • (S22 + S22)2 • K2°2 + 1 • S122 • K102

(23)

K22 0 and K12 0 represent the initial stiffnesses of the mode I and mode II cohesive laws, respectively.

A further relationship is needed to define damage initiation: this is done using a the quadratic damage initiation criterion [24]

The last relationship needed, regards the definition of the critical equivalent opening. Since the area underlying the cohesive law is representative of the critical strain energy release rate, using the Kenane and Benzeggagh (KB) theory [25] the area underlying the mixed mode equivalent cohesive law (req) can be computed as

r, q =Г22 + (Г12-Г,2 )• MM— (25) where (Г22) and (Гi2) are the areas underlying the mode I and mode II cohesive laws, respectively, mm is a mixed mode coefficient depending on the adhesive
and MM is the mixed mode ratio defined as a function of the mode I and mode II strain energy release rates as follows:

G

MM =——- £— (26)

GI + GII

The KB mixed mode fatigue crack propagation model [26] is the first considered, since it is the most general law that can be found in the literature. The fatigue crack growth rate is given by Eq.(1) where this time B and d are functions of the mixed mode ratio MM:

dI, BI and dII, BII are, respectively, the parameters of the Paris law in mode I and mode II; nd, and nB are material parameters. Also other literature approaches were implemented in [19] but they are not considered here for the sake of comparison with Abaqus® VCCT fatigue delamination, where KB is the only mixed mode loading FCG model. Moreover, updating of B and d with MM during propagation has been deactivated since it is not a feature available in Abaqus®.