Силы взаимодействия между коллоидными частицами, проявляющиеся при утоньшении разделяющих их прослоек жидкости, могут как ускорять коагуляцию, так и сильно ее тормозить. Чтобы выяснить1 роль таких прослоек и механизм их стабилизующего действия, рассмотрим их поведение на примере простой схемы, когда прослойка жидкости разделяет параллельные поверхности двух пластинок. В этом случае разделяющая прослойка всюду имеет одинаковую толщину и по краям граничит с дисперсионной средой, в которую погружены обе пластинки.
При достаточно малой толщине прослойки (практически меньше 1 мкм) гидростатическое давление в ней отличается от давления в окружающей жидкости на величину расклинивающего давления, являющегося функцией толщины прослойки. Поэтому для сохранения равновесия, при котором толщина прослойки остается постоянной, к пластинкам необходимо приложить силу, уравновешивающую расклинивающее давление прослойки. Определив значение уравновешивающего давления, можно тем самым найти и расклинивающее давление П. Если гидростатическое давление в прослойке понижено или пластинки притягиваются друг к другу, то расклинивающее давление имеет отрицательное значение.
Рассмотрим природу сил, определяющих расклинивающее давление и его зависимость от толщины зазора между пластинками.
Молекулярные силы притяжения. Прежде всего следует рассмотреть силы молекулярного притяжения, действующие между поверхностями любых тел, как одинаковой, так и различной природы.
Закон молекулярного притяжения всего проще проявляется при взаимодействии пары молекул в отсутствие других молекул, которые могут изменять силу молекулярного притяжения. Как было пбказано впервые с помощью квантовой механики Лондоном, сила притяжения FM меняется обратно пропорционально седьмой степени расстояния г между молекулами, а молекулярная энергия UM притяжения — обратно пропорционально шестой степени расстояния:
С/м = — а/гв (IX, 21)
F„ = — dUJdr — — 6a/r7 (IX, 22)
Знак минус в уравнении (IX, 21) указывает на убывание энергии при сближении молекул; знак минус в уравнении (IX, 22) показывает, что сила притяжения увеличивается при уменьшении
расстояния г. Константа а изменяется в довольно широких пределах в зависимости от природы обеих молекул. Чтобы оценить, насколько велико влияние потенциальной энергии на движение частиц, следует разделить величину UM на энергию теплового движения молекул KT:
Uu___ Ь_
KT r«
Где b = a/kT.
Существенно, что отношение UM/KT становится весьма малым уже при расстояниях в несколько молекулярных радиусов.
Формулы (IX, 21) и (IX, 22) применимы и тогда, когда молекул много, но средние расстояния^между ними велики по сравнению с их радиусами, как это, например, имеет место в газах. В таком случае полную энергию всех молекул можно найти, суммируя выражения (IX, 21) для всех пар молекул. Кроме того, зная поправку в уравнении Ван — дер-Ваальса, учитывающую вза — > имное притяжение молекул, можно найти и значение константы а.
|
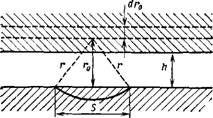
Рис. IX, 4. Схема, поясняющая расчет энергии притяжения к толстой пластинке. |
Подобное суммирование молекулярных взаимодействий в качестве первого приближения можно применить и для вычисления равнодействующей силы, с которой притягиваются друг к другу две пластинки, разделенные плоскопараллельным зазором шириной H *.
|
(IX, 23) |
Определим сначала энергию взаимодействия и’и одной молекулы со всеми молекулами пластинки, расположенной на расстояний г0 от нее (рис. IX, 4). Предполагается, что толщина пластинки много больше не только ft, но и радиуса молекулярного действия г. В этом случае суммирование по всем парам молекул без заметной ошибки можно заменить интегрированием в пределах от г0 до оо:
= qsa dr/rs
Где q — число молекул в единице объема; s — площадь сегмента шара радиуса г, Заключенного внутри объема пластинки, а — константа. Как известно, поверхность шарового сегмента равна:
S = 2лг (г — Го)
Подставляя значение s в уравнение (IX, 23) и интегрируя, получим
Оо
(IX, 24)
Приведенный ниже способ расчета предложен Шелудко.
Для перехода от одной молекулы к единице площади слоя толщиной dr0 следует умножить значение UM на q dr0. Полная энергия притяжения обеих пластинок будет равна:
Оо
= (IX, 25)
H
Отсюда сила притяжения, приходящаяся на единицу площади, определится уравнением:
Р _ Ди" — п Ч2а А IIV 0R
Где А — константа Гамакера.
Измерив силу притяжения пластинок для малых расстояний, можно определить константу а, а также константу Гамакера:
A=rc2q2a (IX, 27>
Значение FM (взятое со знаком минус) выражает слагающую расклинивающего давления Пм, зависящую от молекулярного притяжения.
Впервые
Измерения силы Fм были проведены Б. В. Дерягиным и И. И. Абрикосовой в 1953—54 гг. Позднее их измерения были подтверждены английским исследователем Китченером и голландскими учеными Спарнеем, Овербеком, Де Ионгом и др. Уже на основании данных первых измерений Б. В. Дерягина и И. И. Абрикосовой выяснилось, Что силы притяжения при расстояниях между пластинками больших 300 А оказываются меньше, чем можно было ожидать, исходя из значений а, и убывают с расстоянием быстрее, чем это подсказывает теория.
Это побудило советского теоретика Е. М. Лифшица разработать теорию притяжения тел, состоящих из многих молекул, на новой основе. Согласно Лифшицу, во всех средах существуют беспорядочно флуктурирующие во времени и в пространстве электромагнитные-поля. Распространяясь в пространстве в виде волн, в том числе видимой и ультрафиолетовой области, и проникая в соседние тела, они взаимодействуют с их молекулами. Это взаимодействие и создает силы притяжения между обоими телами в тех случаях, когда разделяющий их зазор достаточно узок. Не приводя сложных расчетов, основанных на квантовой механике, изложим выводы этой теории.
Теория Е. М. Лифшица показывает, что при компактном расположении молекул, имеющем место в твердых телах и жидкостях, энергию взаимодействия нельзя вычислять простым суммированием энергии взаимодействия отдельных пар молекул вследствие отсутствия аддитивности молекулярных взаимодействий. Тем не менее сила притяжения между двумя пластинками зависит от расстояния H так же, как это показано в формуле (IX, 26), однако константа А получает по Е. М. Лифшицу другое выражение. Е. М. Лифшиц связал значение этой константы с оптическими свойствами тел. Следует указать, что формула (IX, 26) справедлива только для расстояний между пластинками не больше, чем 200 А. При больших расстояниях надо принимать во внимание так называемое электромагнитное запаздывание. Оно связано с электромагнитной природой молекулярных сил, которая была предсказана еще русским физиком П. Н. Лебедевым. В силу этой природы молекулярные силы распространяются не мгновенно, а со скоростью света. Не приводя сложные выводы теории, укажем, что в результате электромагнитного запаздывания на расстояниях более 300 А сила притяжения меняется по закону:
Fu = — B[h[19] (IX, 28)
При этом для теоретического определения константы В достаточно знать только диэлектрическую проницаемость тел *.
Табором и другими учеными были измерены силы притяжения твердых тел при значениях ширины зазора, доходивших до 50 А, и для малой ширины зазора была обнаружена зависимость согласно формуле (IX, 26), выражающей йолекулярное притяжение при условии отсутствия электромагнитного запаздывания. Для большинства твердых и жидких тел значения константы А лежат в интервале Ю-14 — 10~12 эрг.
‘ В коллоидной химии большой интерес представляет взаимодействие поверхностей, разделенных жидкой прослойкой, или, иначе, расклинивающее давление жидкой прослойки. Было показано, что уравнения (IX, 26) и (IX, 28) применимы и в этом, более общем случае, причем константы А и В зависят от свойств как обоих тел, так и жидкой прослойки. Последняя может не только уменьшать притяжение поверхностей, но и превращать притяжение в отталкивание. Иными словами, молекулярная или ван-дер-ваальсова слагающая Пм расклинивающего давления жидкой прослойки может быть как отрицательной, так и положительной. Последний случай чаще всего наблюдается для смачивающей пленки, отделяющей пузырек газа от твердой подложки, хотя в этом случае нельзя говорить о взаимодействии двух тел через прослойку жидкости. Отсюда, в частности, следует, что понятие расклинивающего давления шире, чем понятие взаимодействия тел. Уравнение
П =_______
U" 6 nh3
Хорошо применимо для не слишком толстых пленок.
Силы отталкивания. Кроме молекулярной слагающей расклинивающего давления, следует учитывать и другие его слагающие. Из них имеет наиболее общее значение и притом наиболее хорошо изучена сила отталкивания, возникающая при перекрытии диффузных двойных ионных слоев, которые образуются в слоях раствора электролита на границе с поверхностью любой инородной фазы.
Метод расчета этой слагающей впервые был разработан и применен Б. В. Дерягиным и далее усовершенствован совместно с Л. Д. Ландау. Позднее аналогичные расчеты были опубликованы Ленгмюром, А. Н. Фрумкиным, Бергманом, Лов — Беером и Цохе — ром. Изложим принципы этих расчетов для более простого случая, когда потенциал q>0, до которого заряжены поверхности взаимодействующих фаз, мал.
Рассмотрим распределение электрического потенциала <р между заряженными до потенциала фо поверхностями пластинок, погруженными в раствор сильного (полностью диссоциированного) бинарного электролита. Поместим начало координат в середине жидкой прослойки толщиной 2*o, направив ось абсцисс по нормали к поверхностям пластинок
Если заряженная до потенциала фо поверхность граничит с раствором электролита, распределение потенциала в образующемся одиночном двойном ионном слое описывается уравнением:
<р = <роЄ-*г (IX, 29)
Где у. — величина, обратная эффективной толщине двойного электрического слоя, I — расстояние от поверхности пластинок. Согласно этому уравнению при 1 = 0 потенциал ф = фо, а при /-»- оо потенциал ф = 0
В случае, когда в прослойке раствора электролита происходит перекрытие двух двойных ионных слоев, интегралом уравнения d2<p/dx2 = х2ф будет
|
|
(IX, 30)
Где координата х отсчитывается от плоскости, расположенной посередине, между поверхностями обеих пластинок.
Электрический потенциал согласно уравнению (IX, 30) удовлетворяя соотношению d2q>/dx2 = х2ф, одновременно принимает значение фо при х = ±*0.
Чтобы найти электростатическую силу отталкивания между пластинками (равную соответствующей слагающей расклинивающего давления прослойки Пэ), Б. В. Дерягин вычислил разность сил электрических напряжений и гидростатического давления, приложенных к обеим поверхностям — внутренней и внешней — каждой из пластинок.
Эта разность равна:
(IX, ЗІ)
Где є — диэлектрическая проницаемость жидкой прослойки; НІ и На — напряженность электрического поля — с внутренней и внешней сторон пластинки соответственно; р и р0 — соответствующие гидростатические давления.
— Согласно закону Паскаля гидростатическое давление во всех точках покоящейся жидкости одинаково при отсутствии внешних сил. В рассматриваемом случае в точках двойных ионных слоев действуют силы электрического поля, обусловленные зарядами, сосредоточенными в соответствующих местах. От этого гидростатическое давление изменяется, причем давление в какой-либо точке жидкой прослойки по сравнению с равномерным давлением в объеме электролита определяется значением электрического потенциала в рассматриваемой точке. Поэтому, если потенциал на внутренних поверхностях пластин сохраняет такое же значение, что и на внешних поверхностях, р = р0-
Может возникнуть МЫСЛЬ, ЧТО выражение Pi = необходимо дополнить двумя членами, учитывающими влияние так называемых электрострикционных членов, дополняющих Максвелловские выражения для напряжений электрического поля, и влияние аналогичных электрострикционных членов, меняющих распределение гидростатического давления, в частности давление на пластинки. Однако, как известно из теории электричества, оба эффекта имеют противоположные знаки, поэтому компенсируют друг друга
Важно, однако, заметить, что при учете электрострикционных членов избыточное гидростатическое давление в медианной плоскости (х = 0) между пластинками, где Н — 0. не равно Пэ согласно формуле (IX, 31). Следовательно, использованный Ленгмюром и вслед за ним другими авторами способ определения П3 дает совпадающий с (IX, 31) результат только при пренебрежении элек- трострикционными членами
Полагая, что # = —Ду/дх и используя формулы (IX, 29) и (IX, 30) при значениях / = 0 и х = х0, найдем
Я0=Х2Ф2 (IX, 32)
И
Наконец, подставляя значения Н0 и Я, в уравнение (IX, 31), получим:
Д—і +.-««.>» (1Х’34)
Возникающая при перекрытии ионных слоев сила отталкивания (электростатическая компонента расклинивающего давления), пропорциональная квадрату потенциала q>0 поверхностей пластинок, быстро убывает, когда расстояние между пластинками становится существенно больше, чем эффективная толщина двойных ионных слоев.
Расчет давления Па сильно усложняется, когда потенциал фо, возрастай, нарушает условие малости безразмерного потенциала:
Q = ^ (IX, 35)
Где 2—валентность иона; е — заряд электрона.
При этом оказывается, что с ростом £2 электростатическая слагающая расклинивающего давления, возрастав, стремится к конечному пределу. Это на первый изгляд мало понятное явление объясняется тем, что вблизи заряженной поверхности с ростом ее потенциала фо, согласно теореме Больцмана, под влиянием притяжения противоположных зарядов быстро растет пропорционально экспоненте eQ концентрация противоионов В результате действие заряженной поверхности экранируется и потенциал ф с удалением от нее быстро принимает умеренные значения, не увеличивающиеся с дальнейшим возрастанием фо
Сравнительно легко найти, как меняется давление Па в жидкой прослойке, в которой происходит резкое падение потенциала с уменьшением ее толщины 2лг0, но значение £2 во всех ее точках остается достаточно высоким-
N3 = ief—Y-T (1Х’36>
8 V ze)
При малых значениях безразмерного потенциала Q = ze<$o/(kT), получающихся для больших значений хха, давление Пэ убывает пропорционально экспоненте е~2кх
Складывая компоненту расклинивающего давления Пм, зависящую от молекулярных сил (имеющую отрицательный знак), со слагающей, зависящей от перекрытия ионных слоев Пэ (имеющей положительный знак), получают общее расклинивающее давление между пластинками с лиофобными поверхностями, у которых отсутствует сильное взаимодействие с дисперсионной средой. Если пластинки имеют лиофильную поверхность, то вследствие сильного взаимодействия с жидкостью может возникнуть третья, структурная слагающая расклинивающего давления слоев жидкости, структура которых изменена под влиянием лиофильной поверхности. Эта слагающая расклинивающего давления еще недостаточно количественно изучена, и мы ее здесь не рассматриваем. _ . ,
До сих пор мы рассматривали взаимодействие одинаковых поверхностей. Значительно более сложная картина наблюдается, когда жидкая прослойка разделяет поверхности двух различных тел При этом даже если электрический потенциал поверхностей одинаков по знаку, отталкивание на достаточно близких расстояниях переходит в притяжение тем раньше, чем больше различаются потенциалы Когда толщина прослойки станет много меньше толщины двойного электрического слоя 1/х, сила притяжения (—Пэ) составит:
Где ф2 и фі — потенциалы обеих поверхностей
В случае разноименно заряженных поверхностей притяжение будет наблюдаться при любых (но не слишком больших) расстояниях между поверхностями.
Отрицательная молекулярная слагающая расклинивающего давления (равная ван-дер-ваальсовой силе притяжения) для разнородных поверхностей может стать положительной. Таким образом, обе слагающие расклинивающего давления могут иметь как разные, так и одинаковые знаки. Последний случай часто наблюдается для смачивающих жидкостей, для которых молекулярная слагающая положительна так же, как и электростатическая слагающая.
Возвращаясь к рассмотрению тонкого слоя жидкости толщиной 2х0, расположенного между двумя одинаковыми пластинками, изобразим графически зависимость от половинной толщины слоя хп Энергии взаимодействия UM + С’э, вычисленной исходя из строгой теории при условии постоянства потенциала фо = 100 мВ (рис. IX, 5). Показанные кривые относятся к различным значениям концентрации раствора электролита. При малой концентрации электролита (кривая 1) почти при всех значениях толщины слоя превышает отталкивание и только при малых значениях толщины наблюдается результирующее притяжение, которое достигает максимума при некоторой малой толщине. При средней концентрации электролита (кривая 2) потенциальный барьер сдвигается влево, становится круче, уже и выше, при этом при очень большой толщине прослойки наблюдается неглубокая потенциальная яма. При достаточно высокой концентрации электролита (кривая 3) область значений толщины, при которых наблюдается отталкивание, еще больше сдвигается влево и сужается, а правая потенциальная яма углубляется. Наконец, при еще большей концентрации (кривая 4) барьер исчезает и обе потенциальные ямы сливаются.
До сих пор речь шла о взаимодействии пластинок. Подобные случаи реализуются в коллоидных системах, частицы которых имеют плоскую форму, а также в некоторых глинистых минералах при их внутрикристаллическом набухании. Так, было обнаружено, что в кристалле монтмориллонита, насыщенного ионами лития или натрия, помещенном в слабый раствор хлорида натрия, в несколько раз меняется расстояние между слоями, составляющими его слоистую решетку, и соответственно увеличиваются размеры кристалла. Толщины прослоек раствора NaCl, внедряющихся между сетчатыми плоскостями кристалла, могут доходить до 300 А. Таким образом, совершенно очевидна роль расклинивающего давления прослоек в процессе набухания кристалликов монтмориллонита.
В соответствии с теорией набухание тем больше, чем меньше ^концентрация раствора электролита, и процесс прекращается, когда концентрация одновалентного симметричного электролита достигает некоторого предела — порядка 0,1 М. Однако более распространены в природе и технике коллоидные системы, частицы которых имеют более или менее округлую форму. Взаимодействие (например, сила отталкивания F) двух сферических частиц радиусом г на близком расстоянии H0 может быть вычислено приближенно по формуле:
Оо
F = nr^Tldh (IX, 38)
Ka
Где П — расклинивающее давление между плоскими частицами той же природы, разделенными прослойкой той же жидкости толщиной h.
Применяя эту формулу и формулы для вычисления Пм И Пэ, для энергии взаимодействия лиофобных сферических частиц в растворах электролитов можно построить потенциальные кривые, аналогичные тем, которые изображены на рис. IX, 5.
Аналогично меняется характер кривых с изменением концентрации электролита. Таким образом, применяя указанные выше диаграммы, исследование агрегативной устойчивости коллоидных систем сводят к рассмотрению баланса сил молекулярного притяжения и электростатического отталкивания.
Выше мы рассматривали взаимодействие между двумя поверхностями, исходя из представлений о расклинивающем давлении. Однако эти взаимодействия можно интерпретировать, исходя из энергий (или сил), действующих между двумя заряженными плоскопараллельными поверхностями, разделенными весьма малым зазором.
Рассмотрим кратко, не прибегая к использованию довольно сложного математического аппарата [20], окончательные выводы, к которым можно прийти, учитывая энергию взаимодействия Ua между двумя гладкими одноименно заряженными пластинками, находящимися друг от друга на весьма малом рассстоянии.
|
* Рис. IX, 5. Зависимость энергии взаимодействия пластинок UM + U3 От половинной толщины жидкой прослойки х0. Л=»10—12 эрг; фо=100мВ; значення параметра * /— 105; 2-Ю6; 3-Ю7; 4-Ю7.5. |
Энергию электростатического взаимодействия Ua между этими пластинками, отнесенную к поверхности в 1 см2, можно выразить следующим уравнением:
Г, 6 AcRT 2 — U А = — ye Х‘
. Величина у в этом уравнении имеет следующее значение:
Ехр (zF<p0/2RT) — 1 Y = ехр (zF<P0/2RT) + 1
Энергия притяжения Uк, обусловленная действием молекулярных сил меясду пластинками, отнесенная также к поверхности в 1 см2, выражается следуюшш уравнением:
Г/ _________ А
М 12я(2*0)2
Где А — константа Гамакера; 2хо — расстояние между пластинками. —
Энергии Ua и UМ противоположны по знакам, так как в первом случае имеет место отталкивание, а во втором случае — притяжение. Таким образом, общая энергия взаимодействия двух пластинок, отиесеииая к 1 см2 поверхности» в этом случае будет равна:
64CRT „2_-4х*„ Л
U = Y e
48 nxl
В этом уравнении не учитывается компонента, отвечающая структурной слетающей расклинивающего давления слоев жидкости, свойства которых изменены под влиянием поверхностей.
 1 ноября, 2012
1 ноября, 2012  admin
admin 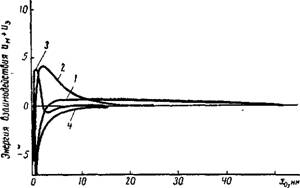
 Опубликовано в рубрике
Опубликовано в рубрике 