Наблюдение за скоростью седиментации в суспензиях, т. е. в дисперсных системах с достаточно большими частицами, облаДающих практически полной кинетической неустойчивостью, позволяет сравнительно легко и удобно определять размер частиц. Применяющиеся при этом методы получили название методов се — димептационного анализа.
Рассмотрим, как оседает в жидкости отдельная частица такой суспензии.
Оседание частицы, очевидно, происходит под действием силы тяжести /, которая с учетом на потерю в весе, по закону Архимеда, составляет:
F = v (р — Po)g
Где V — объем частицы; р — плотность вещества частицы; ро — плотность среды; g— ускорение свободного падения
Оседанию противодействует сила трения f:
Г = Ви
Где В — коэффициент трения между частицей и средой; и — скорость седиментации частицы
Вначале частица движется ускоренно, так как при малых скоростях сила тяжести превышает силу трения. По мере увеличения скорости движения сила трения возрастает и в некоторый момент уравновешивает силу тяжести, вследствие чего частица начинает двигаться с постоянной скоростью. При стационарном режиме оседания, очевидно, должно соблюдаться равенство:
V(p-p0)g = Bu (111,38)
Применительно к сферическим частицам это уравнение принимает вид
Vs»w3 (р — ро) G = бтуи (III, зэ)
Из уравнения (111,39) легко найти скорость седиментации частицы:
2 г2
И=д£-(р-ро)« (III, 40)
Согласно уравнению (111,40) скорость седиментации частицы прямо пропорциональна квадрату радиуса (или диаметра) частицы, обратно пропорциональна вязкости среды и зависит от раз — Вости р — р0 так, что при р ;> р0 происходит оседание, а при Р < ро (например, суспензия парафина в воде) всплывание частиц— обратная седиментация.
Из уравнения (III, 39) легко также найти радиус частицы, зная скорость ее оседания и значение величин r|, р и ро:
V 2 (р — ро) G ‘
Уравнение (III, 39) справедливо для водных суспензий, имеющих частицы размером от 0,1 до 100 мкм, так как для этих частиц время нарастания скорости оседания до постоянного значения настолько мало, что не оказывает влияния на результаты седимен — тационного анализа. Например, время достижения постоянной скорости оседания частиц кварца радиусом 50 мкм в воде составляет 3,4-Ю-3 с, а для частиц радиусом 1 мкм оно равно всего 1,7-Ю-6 с.
К частицам радиусом больше 100 мкм, в обычных условиях оседающим ускоренно, и к частицам радиусом меньше 0,1 мкм, содержащимся в кинетически устойчивых системах, уравнение (111,39) неприложимо. Поэтому обычный седиментационный анализ в этом случае непригоден.
Рассмотрим теперь седиментацию дисперсных систем, состоящих из множества частиц. При этом примем, что частицы в таких суспензиях оседают совершенно независимо друг от друга.
В монодисперсной системе, поскольку скорость оседания одинаковых по размеру частиц одинакова, отстаивание будет происходить равномерно (высота слоя осветленной жидкости пропорциональна времени оседания т). При этом граница раздела отстоявшейся концентрированной суспензии и прозрачной среды будет смещаться на некоторое расстояние. Тогда скорость оседания и выразится уравнением:
М = Я/т — (III, 42)
А радиус частиц уравнением:
R = k Л/WJx (III, 43)
Где
2 (р —’ро) G
По уравнению (III, 43) легко вычислить радиус частиц суспензии по результатам наблюдения за ее оседанием визуально. Скорость седиментации монодисперсной суспензии можно определить, наблюдая за оседанием какой-нибудь одной из ее частиц в микроскоп.
^ При отстаивании полидисперсной суспензии в ртличие от монодисперсной граница оседающего слоя оказывается размытой, так как частицы, имеющие различные радиусы, проходят за одно и то же время различные пути. Поэтому седиментационный анализ полидисперсной системы сводится к определению скорости накопления осадка.
Способы установления зависимости между массой выпавшего осадка т и временем оседания т, графически изображаемые так
называемой кривой седиментации, из которой получают необходимые данные для характеристики полидисперсности исследуемой системы, подробно рассматриваются в практикумах по коллоидной химии. Отметим лишь, что при вычислении размера частиц,
|
Рис. III, 5. Построение кривой распределения. |
Исходя из кривой седиментации, характеризующей содержание в полидисперсных системах частиц различного размера, помимо классического графического метода расчета, предложенного Све — ном Оденом, применяются аналитические методы построения кривых седиментации, разработанные Н. Я. Авдеевым и Н. Н. Цюрупой.
По результатам, полученным при обработке кривой седиментации, обычно строят кривую распределения, наглядно показывающую весовое содержание Q в суспензии различных фракций. Дли этого строят диаграмму, на оси абсписс которой откладывают значения радиусов частиц г, на оси ординат — значения Q/Ar для каждой фракции. Пример такой диаграммы приведен на рис. III, 5. Тогда Q/(Ar—Ar) = Q и весовое содержание каждой фракции выразится площадью соответствующего прямоугольника. Построив такие прямоугольники для всех фракций и соединив плавной линией средние точки их верхних сторон, получают кривую распределения Фракция, отвечающая максимуму кривой распределения, называется преимущественной фракцией полидисперсной суспеизиц, так как очевидно, что частиц, составляющих эту фракцию, в системе больше всего (на рис. III, 5 эта фракция IV с частицами, радиус которых лежит в пределах от и до п).
|
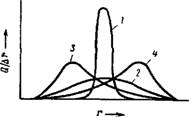
1 — система, наиболее приближающаяся к моиодисперсной; 2—наиболее полидисперсная система; S, 4—системы, содержащие соответственно преимущественно мелкие частицы (максимум сдвинут влево) и крупные частицы (максимум сдвинут вправо). |
|
Рис. III, 6. Типичные кривые распределения: |
Кривые распределения являются важной характеристикой дисперсных систем Чем уже интервал радиусов кривой распределения и чем выше ее макси — чум, тем суспензия ближе к монодисперсной Наоборот, чем кривая более растянута и чем ниже максимум, тем суспензия более полидисперсна. На рис. 111,6 ДЛЯ примера приведены кривые распределения четырех различных типов.
Остановимся теперь кратко на экспериментальных приемах, используемых при седиментационном анализе полидисперсных систем.
|
|
|
|
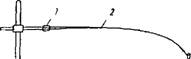
Весовая модификация седиментационного анализа заключается в определении скорости накопления осадка на чашке весов. Для этой цели были предложены седиментационные весы самых разнообразных конструкций. Наиболее распространенными седимен — тационными весами является прибор Н. А. Фигуровского, предложенный им в 1936 г. Этот прибор (рис. III, 7) представляет собою
Закрепленный в горизонтальном положении в держателе штатива J гибкий стеклянный или кварцевый шпиц 2, на конец которого подвешивают на стеклянной нити тонкостенную стеклянную чашечк^~ 3. Расстояние между уровнем жидкости и подвешенной чашечкой обозначено через Н. При погружении чашечки в цилиндр с испытуемой суспензией на чашечке постепенно накапливается осадок и шпиц проги-
|
|
———————————————————- бается. За прогибом шпица
Рис. 111,7. Седиментометр Фигурой- следят при помощи отсчетного ского: микроскопа. Отмечая во време-
1 — держатель штатива; 2 —шпиц; 3 —чашечка. НИ ПЄРЄМЄІЦЄНИЯ КОНЦЭ ШПИЦЭ
По микрошкале, строят график изменения величины прогиба шпица во времени. Так как при прогибе шпица имеет место подчинение закону Гука, то полученный график выражает зависимость массы осадка т от времени т, т. е. M = F(Т). Вместо того, чтобы подвешивать чашечку к концу гибкого шпица, ее можно укрепить "к коромыслу торзионных весов. При этом за накоплением осадка следят по перемещению стрелки на циферблате весов.
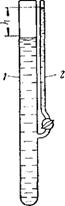
Другой метод наблюдения за ходом седиментации полидисперсных систем, предложен Вигнером в 1918 г. Этот метод основан на измерении гидростатиче — I ского давления столба суспензии при выделении из нее дисперсной фазы в ре — , зультате седиментации. Седиментация по этому методу проводится в специальном приборе — седиментометре Вигнера (рис. 111,8). При закрытом кране, соединяющем оба колена прибора, в широкую трубку 1 заливают суспензию, а в узкую трубку 2 вводят дисперсионную среду, затем кран открывают. Вначале уровень жидкости в трубке 2 выше, чем в трубке 1, так как средняя плотность суспензии обычно больше, чем плотность среды. Однако по мере выпадения дисперсной фазы суспензии и накопления осадка на дне трубки 1, плотность суспензии будет постепенно приближаться к плотности среды и разность уровней жидкости H в обоих коленах будет уменьшаться. Зависимость H от времени седиментации можно использовать для построения кривой седиментации.
Весьма интересный метод седиментационного анализа, хотя и требующий довольно сложного оборудования, разработали Н. А. Фигуровский и Т. Б. Гав-
рилова. Этн авторы применили для оседания дисперсной фазы сконструированные нми автоматические центробежные приборы, позволяющие определять размеры частиц высокоднсперсных систем (до 0,05 мкм прн плотности дисперсной фазы 2—4 г/см3). С помещью этих приборов можно изучать кинетику оседания частиц и затем получать кривую распределения частиц по размерам.
В заключение следует отметить ряд условий, ограничивающих применимость седиментационного анализа. Во-первых, основное уравнение седиментационного анализа (111,39) пригодно только для расчета размера сферических частиц. Для частиц, отличающихся по форме от сферических, уравнение (111,39) позволяет определить только так называемый эффективный, или эквивалентный радиус, т. е. радиус воображаемых сферических частиц, обладающих той же плотностью и оседающих с той же скоростью, что и частицы суспензии. Во-вторых, при седимента — ционном анализе с использованием уравнения (111,39) можно получить правильные результаты только в том случае, если частицы не сольватированы. Понятно, что влияние сольватации будет сказываться в тем большей степени, чем меньше размер частиц. Наконец, в-третьих, седиментационный анализ можно применять только тогда, когда частицы оседают раздельно друг от друга (когда концентрация системы не слишком велика) и когда они не образуют агрегатов.
Ультрацентрифуга и ее применение для дисперсионного
Как уже указывалось, под действием гравитационного поля оседают только достаточно крупные частицы. Коллоидные частицы под действием силы тяжести не седиментиру^от или седиментируют чрезвычайно медленно. Так, частицы кварца радиусом 0,1 мкм проходят при оседании путь в 1 см за 86,2 ч. Однако, заменяя гравитационное поле действием центрифуги с гораздо большим ускорением, в сотни тысяч раз превышающим ускорение свободного падения, можно заставить оседать достаточно быстро и коллоидные частицы. В частности, в центробежном поле с ускорением 105 G та же суспензия кварца должна оседать на 1 см всего за 3 с.
Использовать ультрацентрифугу для определения размера коллоидных частиц впервые в 1910 г. предложил А. В. Думанский. Шведский ученый Сведберг широко использовал эту идею, он разработал. ряд конструкций ультрацентрифуг для определения размера коллоидных частиц и молекул высокомолекулярных веществ, например белков.
|
Рис. 111,8. Седименто — метр Вагнера: 1— трубка для Суспензии, 2 — трубка для дисперсиодной Среды. |
Принципиальное устройство ультрацентрифуги показано на рис. 111,9. На приводимую в движение ось центрифуги 1 надет
ротор 2— массивный диск, в котором имеются радиальные вырезы. В эти вырезы вставляются прочные кварцевые кюветы 3, в которые наливают исследуемую коллоидную систему. Ротор ультрацентрифуги, вращающийся с большой скоростью (десятки тысяч оборотов в минуту), окружен кожухом 4. В отдельных местах кожуха сделаны окошки, соответствующие вырезам ротора. Под нижним окошком кожуха помещен источник света 6, а над верхним окошком кожуха — фотокамера 5. При длительном вращении коллоидные частицы, если их плотность больше плотности
Среды, отбрасываются центробежной силой к периферий. В результате этого в кювете появляется ближе к периферии слой концентрированного золя и ближе к оси вращения — слой осветлившейся жидкости. По мере центрифугирования первый слой уменьшается, а второй—увеличивается, пока не установится седи — ментационное равновесие или пока все частицы не осядут на дно. Путем фотосъемки через определенные промежутки времени можно проследить за передвижением границы между двумя слоями. Схематически эти снимки показаны на рис. III, 10.
При центрифугировании полидисперсной системы четкой границы, конечно, не образуется. Однако полученные сннмки позволяют установить распределение концентраций дисперсной фазы В кювете.
При исследовании бесцветных и прозрачных золей перемещение границы или распределение концентраций в кювете приходится определять не с помощью обычных фотоснимков, а путем наблюдения за коэффициентом преломления золя в различных участках кюветы.
По данным, полученным тем или иным способом, можно вычислить скорость седиментации или найти седиментационное равновесие. На основании этого, в свою очередь, можно рассчитать молекулярный вес или размер частиц, подвергающихся седиментации.
Рассмотрим более подробно определение размера частиц по скорости седиментации в ультрацентрифуге. Для расчетов применимо уравнение, в общем сходное с обычным седиментационным уравнением (111,38). Однако поскольку/-при центрифугировании частицы, постепенно удаляясь от оси вращения, двигаются с переменной все возрастающей скоростью, в уравнении величина и Должна быть заменена на Dx/Dx (где х — расстояние частицы от оси вращения). В то же время из механики известно, что ускорение в поле центрифуги равно ю2х (где со — угловая скорость). Тогда, очевидно, уравнение (111,38) в применении к ультрацентрифуге можно написать следующим образом:
Bdxfdx = V{Р —ро)ю2х (Ш, 44)
Разделяя переменные и интегрируя от Х до х2 и соответственно от 0 до т, можно получить:
Idx/x—‘b-ri*]*
1п(х2/*,) = о(р-ро )<й2х/в (111,45)
Принимая, что частицы имеют сферическую форму, и подставив соответствующее значение для В, получим:
In (X2/Xl) = 2г2 (р — ро) <о2т/(9т|) (III, 46)
Решая это уравнение относительно г, можно написать:
9т, In (^/х,)
2(р — ро)<о2тг 1 ‘
Пользуясь уравнением (111,47), можно рассчитать численный или молекулйрный вес по перемещению в поле ультрацентрифуги сферических частиц на расстояние Хг— Х за время т. Понятно, что для этого необходимо также знать величины г, р, ро и со.
Уравнение (111,45) можно представить таким образом, что В правой части его будут находиться все постоянные величины, характеризующие исследуемую систему:
= 0(Р-РО) =J"onst (ш 48)
Тсо2 В В v ‘
Выражение ln(x2/xi)/(x(o2) называют константой седиментации И обозначают через 5. Константа седиментации может служить Мерой «седиментируемости» данной системы.
|
Ч |
Если известен коэффициент диффузии, то из соотношений = kTjB для диффузии и уравнения 5 = т/В можно исключить
В и найти массу т., а следовательно, и численный или молекулярный вес. Такой способ определения численного или молекулярного веса особенно пригоден для систем, содержащих частицы, сильно отличающиеся по своей форме от сферической или сильно сольва — тированные. Это связано с тем, что величины S я D одинаково зависят от формы и степени сольватации частиц.
Размер коллоидных частиц, как уже указывалось, можно найти не только по скорости седиментации в ультрацентрифуге, но и определяя седиментационное равновесие. Для этой цели применяют центрифугирование при не слишком больших частотах вращения (обычно около 20 000 об/мин), так как иначе превалировала бы седиментация и равновесие не устанавливалось. Численный или молекулярный вес, найденный по седиментационному равновесию, отвечает равновесному распределению частиц в системе, он не зависит от способа достижения этого распределения, и, следовательно, на результатах анализа не может сказываться форма частиц и их сольватация.
Комбинируя определение скорости седиментации с определением седиментационного равновесия, можно найти и кривую распределения частиц, если центрифугированию подвергается полидисперсная система. Сравнение результатов седиментации в ультрацентрифуге по обоим методам позволяет также судить и о форме частиц.
Современная ультрацентрифуга представляет собою сложный прибор, конструкция которого обеспечивает равномерное вращение ротора и отсутствие вибраций, исключает малейшие температурные колебания в кювете и т. д. В новейших ульт^ацентрифугах ротор диаметром всего в несколько сантиметров, изготовленный обычно из хромоникелевой стали, вращается в токе разреженного водорода. Водород, обладающий высокой теплопроводностью, обеспечивает быстрый отвод тепла, выделяющегося вследствие трения, и таким образом уменьшает возможность тепловой конвекции в кювете. Такие ультрацентрифуги приводятся во вращение с помощью масляных турбин. Существуют и воздушные ультрацентрифуги, ротор которых приводится во вращение и поддерживается во взвешенном состоянии потоком воздуха.
Следует отметить, что в последнее время ультрацентрифуги начинают использоваться не только для определения численного или молекулярного веса дисперсных систем, но и для чисто препаративных целей, например, для разделения смесей высокомолекулярных соединений в растворах на отдельные фракции, отличающиеся размером молекул.
 1 ноября, 2012
1 ноября, 2012  admin
admin 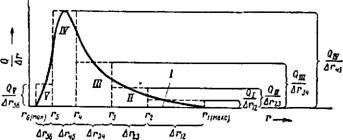

 Опубликовано в рубрике
Опубликовано в рубрике 