Большинство материалов, используемых в качестве клеев, представляют собой полимеры или мономеры, которые превращаются в полимеры в процессе отверждения или вулканизации клея. Полимеры принадлежат к классу материалов, которые можно описать как вязкоупругие материалы, то есть для них характерны свойства как вязкой жидкости, так и упругого твердого тела. П|ючность и эксплуатационные характеристики клеевых слоев в значительной степени зависят от вязкоупругих свойств таких полимеров.
Рассмотрим воздействие синусоидального напряжения, приложенного к Гуковскому или упругому твердому телу. Величина синусоидального напряжения описывается выражением
о(Г) — Оу$іп((оГ), (2.17)
где о(г) временная зависимость напряжения; f — время; со угловая частота приложенного напряжения, измеряемая в радианах в секунду.
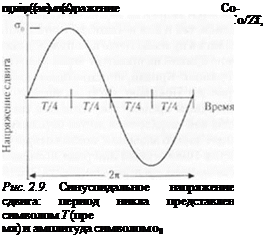
Диаграмма синусоидально приложенной нагрузки представлена на рис. 2.9, где о0 представляет собой амплитуду напряжения. Уравнение (2.17) подставлено в уравнение (2.3), чтобы показать временную зависимость деформации:
![]() (а,//0 sill(<l)/) — e(f).
(а,//0 sill(<l)/) — e(f).
 |
|
Однако учитывая что
Энергия, которая поглощается за один никл синосуидалыгого напряжения, может быть рассчитана интегрированием мгновенной скорости поглощения энергии в течение полного цикла. Мгновенная скорость поглощения энергии ^ описывается следующим выражением:
$-o(Sc/8f). (2 21)
Расчет выполняется ступенчатым методом для определения энергии, поглощенной в каждой области цикла. 1 Іачальньїй участок кривой, представленной на рис. 2.9, делится на четыре временных интервала Т/Л. где ‘/’представляет период цикла. Для угловой частоты полный период составляет 2л радиан. В результате ннтсгри|х>вания уравнения получаем следующее выражение:
7/4 к/2«
ДН= j Ijit — о0Е0ш J sin(oy )oos(cj/)(fr (2.22)
Максим;ілі. пая накопленная энергия упругого дс<|юрміфования в материале, под вергнутом воздействию синусондального напряжения, описывается уравнением:
S=M-EtJ/2. (2.23)
Интегрирование выполняют для всех четырех участков цикла. Для областей
цикла, которые имеют восходящую кривизну, характерны положительные значения £е0г/2, в то время как области кривой с отрицательной кривизной характеризуются отрицательным значением Ег/‘/2. Указанный выше полный цикл ASw равен нулю. В случае упругого материала вся энергия, поглощенная образцом, восстанавливается при снятии нагрузки с образца.
Рассмотрим ньюгономскую жидкость, которая моделируется пунктирной линией, показанной на рис. 2.7. В этом случае ситуация существенно меняется. Уравнение (2.16) описывает реакцию ньютоновской жидкости на воздействие напряжения. Если деформация представляет собой синусоидальную функцию, то можно записать следующее выражение:
с(0 — е0 sin(o»f). (2 24)
Это уравнение, описывающее деформацию, позволяет рассчитать скорость деформации, которая введена в уравнение (2.16). Таким образом, получаем выражения:
(6с/Ы) — ес со cos(cof) (2 26)
и
а(Т) — ns, <■> cos(cor). (2.26)
На рис. 2.10 представлен график зависимости функции напряжения и деформации для ньютоновской жидкости, подвергающейся воздействию синусоидальной дес|юрмации.
|
Рис. 2.10. График, покалывающий различие между напряжением и деформацией при сдвиге для ньютоновской жидкости |
Необходимо отметить, что кривая для ньютоновской жидкости сдвинута по фазе на 90“ по сравнению с тем состоянием, которое можно было бы прогнозировать для щюизводной синусоидальной функции. Аналогичное представление справедливо для расчета рассеяния энергии ньютоновской жидкостью в течение одного цикла кривой. Этот расчет выполняется гем же методом, который описан выше для упругого твердого тела в результате деления периода на четыре части и интегрирования с, для каждого сегмента. В этом случае
(2 27)
Интегрируя это выражение, получаем
(228)
для 1 /4 периода и для всего периода
яцшс/ (2.29)
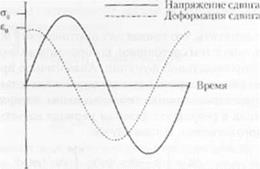
Таким образом, ньютоновская жидкость рассеивает энергию при каждом цикле в отличие от линейно-упругого материала (пружины). который накапливает энергию и высвобождает ее во время каждого цикла. Деформация в случае упругого твердого тела находится в одной фазе с напряжением, в то время как для вязкой жидкости напряжение и деформация сдвинуты по фазе на 90’. Исходя из приведенного выше анализа, можно п]»сдположить. что для вязкоупругого материала характерна такая реакция на приложение нагрузки, при когоіюй фазы напряжения и деформации не совпадают, однако это различие составляет менее 90′. Такое состояние показано на рис. 2.11. Соот веге і вующая функция деформации представлена следующим выражением:
с — е,, sin((of). (2.30)
Соответствующее напряжение не совпадает по фазе с деформацией при угле сдвига фтз б, поэтому можно записать
о — o(1sin(<j* t S). (2.31)
Используя тригонометрическое равенство
sin(a + (1) — sin a cos p + cos a sin p (2.32)
и умножая это выражение на тождество к /с0. получаем следующую зависимость:
а — (ee/cft) cos(6) i:0sm((.v) * (о0/) sin(6) c()cos (tor) (2.33)
Первый член приведенного выше уравнения содержит синус угловой частоты. Этот член описывает вклад напряжения, которое находится в одной фазе с деформацией. Второй член этого уравнения содержит косинус угловой частоты и описы-
|
Рис. 2.11 Характеристические функции напряжения в деформации для вязкоупругого ма термала Необходимо отметить, что фазы напряжения и деформации не совпадают и угол сдвига фат составляет менее 90" |
васт вклад напряжения, которое на 90” не совпадает с фазой деформации. Каждый член этого уравнения имеет также составляющую (а^/гД cos 6. Из уравнения (2.3) видно, что зта составляющая представляет собой именно модуль, умноженный на какой-то показатель. Значения модулей могут быть вычислены по уравнениям
£* — (ао/е0) cos б (2.34)
и
![]() Е’ ~ (о„/с0>sin 6-
Е’ ~ (о„/с0>sin 6-
ІІервмй на них можно назвать «совпадающим по фазе* модулем, а второй — «несовпадающим по фазе» модулем. Необходимо отметить, что в данном случае эти модули обозначены символом И, который свидетельствует о том, что экспериментальные исследования проводились при воздействии растягивающей нагрузки. Аналогичный ряд значений модулей может быть получен в результате экспериментов при воздействии усилия сдвига. В этом случае модули будут обозначаться символами С и С".
Выше были приведены уравнения для расчета накопленной или рассеянной в течение какого-либо цикла энергии как для упругого твердого тела, так и для нью тоновской жидкости. Применительно к вязкоупругому материалу аналогичное выражение имеет следующий вид:
Используя тригонометрическое преобразование, аналогичное уравнению (2.32). и выполнив интегрирование выражения, получаем
АН*-«ууиіп*. (2 37)
Умножив это уравнение на тождество е^/е„ и используя определение, приведенное в уравнении (2.35). находим, что:
ЛН (2.38).
Это выражение относится к общей энергии, потерянной во время какого-либо цикла воздействия нагрузки. Оно объясняет, почему Е" называют модулем потерь материала. Е связан с находящейся н фазе (упругой) реакцией материала, при которой энергия накапливается в течение одной части цикла и выделяется в процессе другой части цикла. Е представляет собой динамический модуль упругости вязкоупругого материала.
Другой важной величиной является отношение динамического модуля упругости к модулю потерь. Тангенс 8 определяется выражением
tnn6 = sin 5/cos б. (2.39)
Из уравнений (2.34) и (2.35) видно, что sin8 — e0F’/o(l и cos8 — е0Р/о<г Выполнив эти подстановки, получаем
![]() tan б — Е’/Е.
tan б — Е’/Е.
Исходя и:* энергетического подхода к полученным в данной работе уравнениям для символов Е и И", можно также показать справедливость следующего выражения:
tan « = (1 / 2л) • ((241)
Таким образом, tan б представляет собой отношение общей энергии, потерянной за один никл (связанный с модулем потерь), к энергии, накопленной в течение 1/4 цикла (связанной с динамическим модулем упругости). В последующих главах будет показано, что все указанные параметры оказывают существенное влияние па использование полимеров в рецептурах клеев.
Приведенное выше описание вязкоупругих свойств материалов, когда они подвергаются воздействию синусоидальных напряжений или деформаций, должно быть хорошо знакомого инженерам — механикам и инженерам-элсктрикам. Это описание абсолютно аналогично описанию проблем, связанных с генератором затухающих колебаний в механике и резисгнвно емкостным контуром в электронике. Углы сдвига фаз имеют одинаковые значения, a tan б имеет значение, аналогичное количеству электричества Q контура.
 5 сентября, 2015
5 сентября, 2015  admin
admin 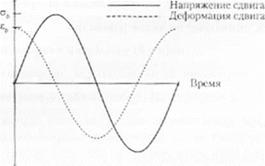
 Опубликовано в рубрике
Опубликовано в рубрике 