В настоящем разделе рассматриваются некоторые ил наиболее часто используемых образцов для испытании при раскалывании или определении трещиностойкости. Необходимо отметить, что процессы разрушения могут начинаться в материале или клеевом соединении различными способами, которые известны как виды разрушения. Наиболее общим тином разрушения является расслаивание и нот вид разрушения называют Тни I. Характер расслаивания был показан ранее на рис. 2.3 и повторно приведен на рис. 3.1G. Следующий тип разрушения, получивший обозначение Тип II. представляет собой сдвиг и этот тип аналогичен приложению усилия сдвига, показанному на рис. 2.2, за исключением того, что в теле образца создана трещина. Последним типом разрушения является раздир[12] или Тни III. Раздир образца может быть представлен как страгиванис лицевых сторон материала выше и ниже трещины во взаимно противоположных направлениях, характер которого также показан на рис. 3.16. Для обозначения данных типов разрушения использованы римские цифры и обычно их приводят в виде подстрочных индексов для скорости освобождения оперши де<!юрмацни. Необходимо заметить, что наименьшее значение скорости освобождения энергии дсч])ор. мациі< почти всегда соответствует разрушению Типа I Рассматриваемые в данной работе образцы относятся исключительно к разрушению Типа 1 и в данном случае скорость высвобождено энергии деформации обозначается символом :б;. При проработке другой литературы, относящейся к данному вопросу, необходимо учитывать вид разрушения.
|
|
|
|
Tim III
htr?. 16. Схематическое изображение трех видов рарушеппя Тип I известен как расслаивание; Тим 11 — как сдвиг, Тип 111 — как |>аздир
Самым простым образцом, позволяющим правильно воспроизводить и анализировать характер разрушения, является одііо[юднмй образец в <|юрме двух консольной балки Такой образец, регламентируемый стандартом ASTM 03443, схематично показан на рис. 3.17. В данном образце субстраты однородны по <|юрме и профилю поперечного сечения. Форма этих образцов обычно представляет собой в сечении
квадрат размером 25.1 х 25.4 мм. Первоначально в край образца вводят «бритвенное лезвие для того, чтобы инициировать появление краевоіі трещины в клеевом соединении. Перед началом испытания лезвие удаляют на образца. К краю образца прикладывают нагрузку одним из указанных ниже способов. Наиболее часто в образце (рис. 3.17) сверлят отверстия и. используя зтн отверстия, образец закрепляют в зажимах разрывной машины. При приложении нагрузки происходит распространение начальной трещины. Одним из измеряемых параметров является перемещение образца, определяемое ходом ползунка разрывной машины; другой представляет собой зависимость длины трещины от величины нагрузки. Этот метод является в значительной степени достаточно сложным и требует применения либо быстродействующей фотосъемки, либо закрепления соответствующих датчиков на клеевом соединении. Например, одним из способов является нанесение с определенным шагом токопроводящей краски на боковую поверхность клеевого соединения и измерение длины трещины по величине последующего разрыва проводящего пути, образованного полосами краски.
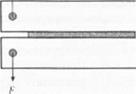 |
F
l*u( ‘}. 17. Образец двухконсольион балки
3.5.1.2. Линейно-упругая механика разрушения образца в виде двухконсольной балки
Переписав уравнение (2.12) относительно разности максимального и минимального значений силы п деформаций, получаем
![]()
![]() U/-50 1 (IW+D6F-г 5F8D) ■
U/-50 1 (IW+D6F-г 5F8D) ■
^ 2 2
Это уравнение может быть представлено в следу кнцем упрощенном виде:
V =—(Fbl)-D6F).
‘ 2
Подсганляя уравнение (3.32) в уравнения (2.13) и (2.14). получаем
Данное уравнение представляет собой выражение для определения скорости освобождения энергии деформации исходя из измеряемых параметров F и I) и пх производных относительно длины трещины. Можно п|>евратить это уравнение в равенство и в результате этого перевести измеряемые параметры Г и I) п F и D. пред-
стапляющие собой критическую силу и деформацию при росте трещины. Таким образом, получаем следующее выражение:
![]() (3.34)
(3.34)
Анализ рис. 2.6 показывает, как можно преврати. уравнение (3.34) в выражение. которое позволяет определить одну переменную величину вместо двух. Если на осях рис. 2.6 отложить значения напряжения и деформации, то угол наклона кривой будет представлять модуль упругости. Однако, так как на этих осях отложены значения силы и перемещения, можно только говорить о том. что наклон кривой описывает жесткость данного определенного образца. Обратная величина жесткости определяется как податливость образца. Величина С — D/F, так как в данном случае рассматривается линейно упругий материал (в этом выражении величина С представляет собой податливость). Используя данное выражение, можно следующим образом уп|км:тить уравнение для критической силы и перемещения при росте трещины:
!>1±ь£
2п С1 Ъа~2п «о ^
Последнее уравнение играет важную роль, так как величина ЬС/Ъп может быть либо рассчитана, либо измерена. Для случая двухконсольных балок величина 5С/5« может быть определена в соответствии с теорией балки. Для балки, имеющей постоянное поперечное сечение, высоту h. ширину w и модуль упругости изменение податливости в зависимости от длины трещины описывается выражением:
![]() (3.36)
(3.36)
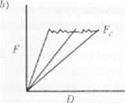
Это уравнение показывает, что величина 8(?/б« может быть постоянной, если выражение, приведенное в скобках уравнения, является постоянным. Такой вывод оказался справедливым, н исследователи предложили использование скошенных по высоте или ширине двух консольных балок. Скошенная по высоте лвухконсольная балка была использована для исследования клеевых соединений алюминиевых субстратов, в то время как скошенная по ширине двух консольная балка использовалась, аля исследования клеевых соединений углепластиков [9). Взави — симости от модуля Юнга субстратов используют различиме уклоны для получения образцов соответствующих размеров. Определение ‘S(i оказывается более простой операцией при использовании скошенных балок, так как критическая скорость освобождения энергии деформации прямо пропорциональна критической силе при расп[м>странении трещины. 11л рис. 3.18 показано сравнение графиков зависимости /•’от D при определении Ък для ровного и скошенного образцов двухкоисольной балки.
Анализ кривых, приведенных на двух графиках рис. 3.18, показывает разницу между результатами испытаний двух образцов. На рис. 3.18, а представлены результаты испытания, полученные для ровного двухконс олыюго образца. Каждый прямолинейный отрезок демонстрирует нагружение образца в начальный момент
 |
 |
Рис. 3.1ft. Схематическое изображение кривых «сила-перемещение*. измеренных на об р<ице двухконсолыюй балки: а — приведен результат для ровной двухконсоль ноіі балки, b для скошенной двухконсолыюй балки. К данном случае очевидно, что критическая сила для роста трешины легко определяется но кроной «сила перемещение» для двухконсолыюй балки
рап1|нн~грансния трещины. Когда образец подвергается повторному нагружению, податливость образца изменяется (длина плеча рычага увеличивается) и кривая повторного нагружения имеет другой вид. В каждом случае при измерениях получают различные значения Г. соответствующие тому же значению (б,, которое может быть рассчитано но результатам каждого измерения F, когда величина Г преобразована относительно 6С/Ъа. Из рис. 3.1ti, b очевидно, что для скошенного образца характерно постоянное значение /•’ независимо от длины трещины в процессе испытания. Применение скошенного образца предоставляет возможность для непосредственного измерения значения *8,.
 11 сентября, 2015
11 сентября, 2015  admin
admin 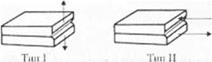
 Опубликовано в рубрике
Опубликовано в рубрике 