Предыдущая глава является базой для разработки и получения представлений о методах определения физических свойств материалов клеевых слоев и клеевых соединений. Основной задачей испытания материала является оценка его поведения при растяжении, сдвиге и расслаивании. В настоящей главе рассматриваются рал личные образцы, описанные в специальной литературе, которые используются для испытаний клеевых соединений. Глава состоит из отдельных разделов, посвященных определенному типу механических испытаний. В каждом разделе приведено общее описание метода испытаний с рекомендациями по правильному проведению испытания. В двух методах испытаний рассматривается изгиб балок для анализа напряженного состояния в клеевом слое’ и субстрате. Этот анализ показывает, что необходимо исключать, если это возможно, некоторые виды нагружения клеевых соединений. Необходимо предупредить, что данная работа не является каким-либо руководством для конструктора. Ее цель заключается в том, чтобы дать полезные рекомендации о правильной подготовке образцов клеевых соединений и показать, какие могут быть получены основные данные об эксплуатационных характеристиках клеевых слоев. Значительная часть данной главы рассматривает методы испытания клеевых соединений, описанные в изданиях Американского общества по испытанию материалов (ASTAf) 111. Описанные в настоящей главе методы испытаний используются для оценки свойств соединений на основе конструкционных клеев, [ихншовых клеев, конструкционных клеев для древесины, клеев-расплавов и других типов клеев. Однако существует также ряд методов испытаний, которые важны для оценки свойств липких клеев (см. гл. 9).
В данной главе рассматриваются следующие основные вопросы, а именно:
• понять, какая полезная ннс}юрмация может быть получена из результатов каждого испытания;
• разработать подход к использованию теории балки для получения представления о напряженном состоянии клеевых соединений;
• предложить практические рекомендации но оптимальным с пособам подготовки клеевых соединений ряда образцов.
1. Объясни і ь различие между нагрузкой и напряжением. Почему такое нредстав — ленне оказывается важным при рассмотрении свойств материалов?
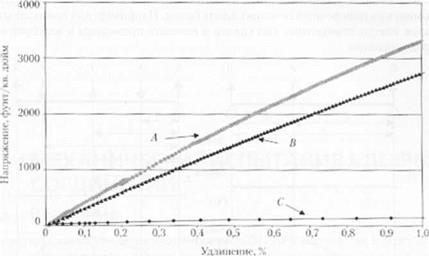
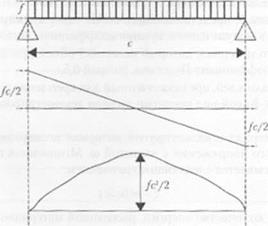
2. Рассмотреть приведенные кривые «папряжение-деформация* для трех ти нов материалов клеевых слоев. На первом ірафике приведена полная кривая «напряжение деформация*; иа втором увеличенное изображение нижнего участка деформационной кривой.
|
Удлинение, "о |
|
|
</) Вычислить модуль Юнга и МПа для каждого материала клеевого слоя. (Для того чтобы 1Н*]к*вссги значение фунт/кв. дюйм в МПа, умножить полученную величину на 0.006897.)
b) Какая деформация является предельной .тля каждого материала?
c) Какой из полимеров считается жестким или похожим на кожу? Почему?
<0 Какой клеевой слой « читается хрупким? Почему?
г) Какой клееной слой считается пластичным? Почему?
/) Для образца В, представляющего собой отвержденную эпоксидную смолу, определить модуль сдвига, приняв коэффициент Пуассона равным 0.32.
3. Показать, что материал, который не меняет объем при деформировании, должен иметь ко. и|)фіінііент Пуассона, ранный ОД А. Вы разработали клей, предназначенный для крепления плиток к верт икальной поверхности. Какой вид реологии должен демонстрировать этот клей и почему?
5. Упругий материал и вязкоупругий материал подвергаются воздействию синусоидального напряжения с частотой со. Мгновенная скорость потлощения энергии описывается следующим уравнением:
с, = o(«V. &о
Рассчитайте количество энергии, рассеянной материалом в течение всего периода воздействия нагрузки.
6. К балке приложена равномерная нагрузка, равная g килограмм на метр длины. Какая связь существует между моментом и нагрузкой? (Эта зависимость не должна представляться в интегральном виде).
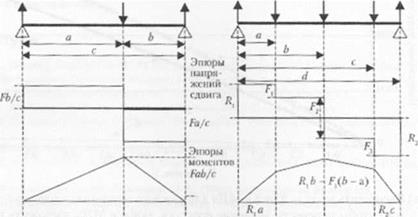
7. Для любой задачи, связанной с анализом статически определенной балки, мож но построить диаграмму сдвига и момен т. Одним из таких подходов является
использование уравнений статического состояния для определения сдвига и момента на поперечних сечениях вдоль балки. Например, для показанных трех балок эпюры поперечных сил сдвига и момента приведены в алгебраическом представлении.
|
Л, F R, R, F, F, F, R,
|
Как приведенные эпюры поясняют уравнения, предложенные для анализа связи между сдвигом, моментами и нагрузками? [10]
|
Рлпноисрно іпспрглслсшіая нагрузка,/
|
В данной главе определены и рассмотрены многие свойства материалов, которые используют в качестве основных критериев при обсуждении положений, представ ленных в последующих главах. В частности, рассмотрены такие представляющие особое значение параметры, как модуль Юнга и модуль упругости при сдвиге, ко- эффицисит Пуассона, энергия деформации и критическая скорость релаксации энергии сдвига. Кроме того. и|к*дставлены свойства жидкостей и экспериментально определены их вязкостные характеристики. Описаны свойства жидкостей при различных скоростях сдвига. Определены такие важные вязкоупругие характеристики
как динамический модуль упругости и модуль потерь. И наконец, в соответствии с предложенным Тимошенко подходом выполнен анализ балки при воздействии напряжения изгиба. Одним из основных элементов при анализе поведения балки было использование описанных выше в данной главі — параметров удлинения, модуля упругости при растяжении и подчиняющихся закону Гука свойств материалов при сдвиге и раст яжении.
Barnes 11. A., Hutton J. F. and Walters К. An Introductum into Rheology (1089) Elsevier. Amsterdam.
Ferry J. L) Tin — Veuoelastu Properties of Polymers (1980)John Wiley, New York.
Heark-J. W. S. Polymersandtheir Aupnrira Vol. 1 (1982) Fllis Horwood, Chichester. I’k Kinloch A. J. and Young R. J. Fracture Behavior of Polymers (1983) Elsevier. New York.
Nielsen I. E Mechanical Ihopetlies of РЫутеп (1962) Reinbold Publishing Corp., ( hapman and Hall, New York.
К a off A. L Materials Science (1973) Рп-ntice-Hall. Englewood Cliffs, NJ.
ShriglevJ E. and Mischke C. R. Mechanical Engineering Design (5th Ed.) (1989) McGraw INI Inc. New York
Thomas <1. И Calculus and Analytical Chemistry. VK F, d. (1969) Addisnn-Wesley. Reading MA.
Timoshenko S the Strength of Materials, p. irr 1. Chapters 1 -5 (1995) Г). Van Noslrand. Princeton. NJ.
Клеевые соединения изготовляют, используя один или несколько субстратов и клей. В тех случаях, когда предпринимаются попытки отделить субстрат от клеевого слоя или клеевое соединение подвергается нагружению, субстрат выступает в роли бал ки, подвергающейся воздействию изгибающих напряжений. Некоторая часть образцов для испытания клеев, описываемых в следующей главе, рассматривается как субстраты, представляющие собой балки, подвергнутые воздействию сдвигового напряжения, или как балки на упругом основании. Поэтому целесообразно рассмотреть в данной главе основные теоретические положения механизма изгиба балок. Большая часть рассматриваемых в настоящем разделе материалов основана на работе Тимошенко *The Strength of Materials*.
Анализ изгиба балок, которые представляют собой объекты, находящиеся в равновесном состоянии, основывается на законах динамики Ньютона. Очевидно, что тело, находящееся в равновесном состоянии, обладает статическими свойствами. Сумма сил, приложенных к этому телу, должна стремиться к нулю, и сумма изгибающих моментов (или просто моментов), приложенных к этому телу, должна равняться нулю. В математическом изложении такое положение может быть записано в виде [9]
Каждое из этих уравнений может быть записано в виде серин уравнений для любой системы координат, поскольку они представлены в векторной форме. Например. уравнение для внешних сил можно записать в декартовой системе координат следу ю щи м образом:
IF-IF-IF-O. (2.44)
Аналогичный ряд уравнений может быть предложен для описания моментов.
Для того чтобы понять правомерность приложения указанных уравнений к теории изгиба балок, рассмотрим простую балку на опорах, показанную па рис. 2.12. В данном случае F действующая в плоскости сила и Fy — противодействующая сила. Мри анализе статических характеристик этой балки разделим се на две части по линии п-Ь. Рассмотрим воздействие левой части балки на правую, которые разделены линией а Ь. Анализ статического состояния показывает, что усилие и изгибающий момент могут заменять любую систему параллельных сил. Поэтому для правой стороны балки можно написать
у-рщ-р1-р, <2-45)
и
Л/ — х — F, (.г — рУ F, (г — q). (2.46)
Сила V действует вдоль линии а Ь. В случае балки, находящейся в устойчивом состоянии, силы в правой части балки должны уравновешивать V и Л/. Представим бесконечно малый элемент в области п-Ь. В этом случае силы н моменты действуют так, как показано на рис. 2.13.
При этом длина плеча приложения силы описывается выражением
dM — Mix. (2.47)
которое может быть преобразовано следующим образом:
dM/dx = V. (2.48)
Таким образом, скорость изменения момента вдоль балки равна усилию сдвига. І Іредположим, что распределенная нагрузка полностью действует вдоль балки так, что сила /прикладывается равномерно на единице длины dx. Рис. 2.12 следует изменить, чтобы показать воздействие этой силы. Усилие сдвига должно возрастать
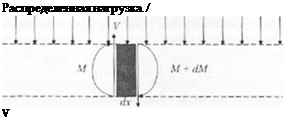 |
hit.’2.13. Бесконечно малая часть Балки dx в области линии ч Ь (см рис. 2.12). Силы на одной стороне балки должны уравновсшипаться силами, действующими на другой ее стороне. Однако из-за расстояния dx момен г меняет свою величину на d1
от левой стороны элемента к нраноіі стороне на величину/. Следовательно, можно записать следующее выражение:
dV —-fdx. (2.49)
которое может быть преобразовано следующим образом:
d’/dx — -/• (2.50)
Это уравнение показывает, что в случае силы, равномерно распределенной вдоль балки, скорость изменения сдвигающей силы с изменением расстояния равна величине нагрузки на единицу. пины. Уравнения (2.48) и (2.50) представляют собой основные критерии теоретических представлений об изгибе балок.
 |
 |
Два вопроса, которые целее ообр;гзно рассмотреть в данноіі главе, свяааны с определением момента инерции балки и уравнениями для оценки прогиба балки. Эти уравнения играют определяющую ролі, при анализе состояний, связанных с изгибом субст ратов в клееных соединениях. Два таких примера рассмотрены в следующей главе.
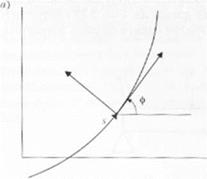
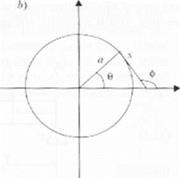
1*ис. 2 I I Кривая < проведенной к ней касательной, линейный сег мен i л и угол о гя); окружность н переменные радиус кривизны и радиус окружное ги {Ь)
Для тот чтобы получить представление о рассматриваемых в последующих разделах результатах анализа, необходимо вспомнить некоторые положения аналитической геометрии. В частности, необходимо вспомнить о связи между кривизной и радиусом кривизны. Рассмотрим рис. 2.14. я. На этой обобщенной кривой показано построение угла ф и длина s дуги. Угол ф образован касательной к кривой и осью х. Кривизна описывается следующим уравнением:
![]()
![]() </о|
</о|
(Is І
Формула для расчета кривизны может’быть после взятия производной получена в следующем виде:
|А|
![]()
![]()
Рассмотрим рис. 2.14. Ь, па котором показаны те же параметры для окружности. 13 данном случае можно записать следующее уравнение
где а — радиус.
Кривизна окружности являет ся обратной величиной се радиуса. Для любой кривой можно начертить соприкасающуюся окружность, кривизна которой совпадает с. кривизной кривой в любой се точке. Затем можно определить радиус кривизны г общей кривой в заданной точке, который является также радиусом соприкасающейся окружности. Для соприкасающейся кривой можно записать следующее выражение:
ds — (uh). (2.54)
где приведенные параметры показаны на рис. 2.14, Ь.
Рассмотрим рис. 2.15. У балки, которая не подвергается воздействию каких-либо сил, отсутствует прогиб. Проведем воображаемые линии вдоль балки. Проведем линии перпендикулярно длине балки. Приложим к балке усилия, независимо от того являю! ся ли они распределенными или точечными нагрузками. Палка принимает какую-то «[юрму, тогда как воображаемые линии описывают отмеченное выше изменение формы или ориентации. Как показано на рис. 2.15, воображаемые линии, нанесенные перпендикулярно длине балки, поворачиваются в направлении поверхности. к которой приложена сила. Воображаемые линии, проведенные параллельно длине балки, остаются параллельными относительно поверхностей балки при малых іцюгибах но длине балки. Однако эти линии принимают такой же радиус кривизны, который принимает балка иод воздействием приложенного усилия. Длина параллельных линий изменяется. В центральной части балки существует линия, длина кото|юн не меняется. Такая линия называется нейтральной осью. Выше нейтральной оси балки линии становятся короче (линии находятся в состоянии ежа-
|
О
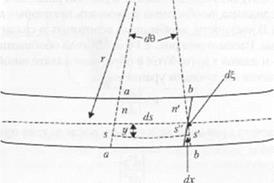
Рис. 2.15. Схематическое изображение прямоугольной балки постоянного сечения и состоянии чистого изгиба. Балка подпергается воздействию какой-то силы или системы сил, которые приводят к появлению момента А/. Линии а-а и b-b перпендикулярны оси балки и взаимно параллельны. После приложения нагрузки линии спутаются перпендикулярными нейтральной оси балки, но теряют взаимную параллельность. Материал верхней части балки находится в состоянии сжатия, в то время как нижняя часть балки — в состоянии растяжения. Длина нейтральной оси и п’ не изменяется. Линия s-s’ показывает линию материала в нижней части балки, которая находится в состоянии растяжения и испытывает удлинение. Вдали от балки показана начальная точка отсчета О; изогнутая балка имеет радиус кривизны г. (Схема перепечатана из работы Тимошенко с разрешения издательства V(uisn<onh Publishing Со.) |
тия), в то время как ниже нейтральной оси линии удлиняются (линии находятся в состоянии растяжения). Даже несмотря на то что рис. 2.15 представлен в идеализированном виде, установлено, что такое положение применимо при решении задач для любой балки. Далее можно, используя рассмотренные ранее в данной главе параметры механических свойств материала, проанализировать деформированное состояние балки.
Для определения деформированного состояния воображаемых линий ниже нейтральной оси (линий в состоянии растяжения) используется геометрический подход. Это трудно представить визуально, так как начальная точка отсчета удалена от рассматриваемых воображаемых линий. Проведем линию n’-s. которая параллельна линии а-а. Рассматривая угол < пОп находим, что этот угол анатогичен углу < поэтому
є — (sY’ypm’)- у/г, (2.55)
где s’s" и пп’ — обозначают отрезки линий, представленных на рис. 2.15; у — расстояние от нейтральной оси до рассматриваемой воображаемой линии; г — радиус кривизны прогиба балки.
В качестве вто|юго варианта можно использовать приведенные выражения для определения удлинения «нитевидных линий», удаленных от нейтральной оси. Используя уравнение (2.54 ), можно записать
ds — rd0. (2.56)
где ds — длина дуги вдоль нейтральной оси.
Так как линии ns и n’s’ взаимно параллельны, то угол dZ. аналогичен углу г/0. Таким образом, получаем
dx — ydO, (2.57)
где у — расстояние рассматриваемой нитевидной линии от нейтральной оси; dx — приращение длины рассматриваемой нитевидной линии.
Из определения удлинения очевидно, что
к — dx/ds. (2 58)
І Іодставив уравнения (2.56) и (2.57) в уравнение (2.58), получаем:
с — dx/ds — ydO/rdO — y/r. (2.59)
Согласно закону Гука для упругих материалов имеем
я — Е(у/г). (2.60)
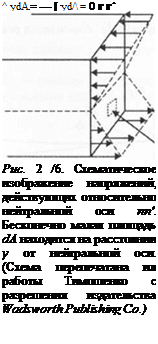
Для любой плоскости, проведенной через балку, должен существовать какой — либо момент, сформированный вокруг нейтральной оси. На рис. 2.16 приведено схематическое изображение такого состояния. По отношению к нейтральной оси величина этого момента должна быть равна нулю, так как балка находится в равновесном состоянии. І (оэтому сила на бесконечно малой величине площади dA описывается выражением odA — (Ey/r)dA и общий момент, действующий на поперечное сечение балки в направлении х, должен быть равен
 |
||
(2.61)
Приведенное уравнение определяет положение нейтральной оси. Момент силы, действующей на площадь dA в направлении у относительно ней тральной оси. равен
(Ey/r)ydA. так как плечо силы равно расстоянию у от нейтральной оси. Сумма :>тих сил должна быть такой, чтобы уравновесить внешний момент. Следовательно:
(-V2dA = — f у1 dA = М = ^ . (2.62)
J г г1 г
где / — интеграл от у’ на всех бесконечно малых площадях, называемый моментом инерции балки; произведение £7 называют жесткостью балки при изгибе.
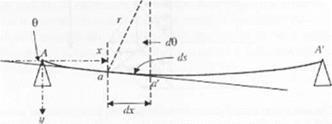
Последняя задача, рассматриваемая в данной главе, связана с выводом уравнений для определения прогиба балки под нагрузкой. І Іекоторис из отих уравнений были приведены в предыдущем разделе; в настоящей главе выполнен более тщательный анализ. 11а рис. 2.17 представлено схематичное изображение таком ситуации.
Для того чтобы определить кривую прогиба для такой балки, необходимо, в первую очередь, принять, что изгиб зависит исключительно от величины внешнего изгибающего момента М в рассматриваемой точке. Воспользуемся уравнением (2.62), то есть выражением 1 /г — Л///:/. Для оценки кривизны используется геометрический метод. Для анализа выбирается малый участок балки п-п’. Вычерчиваем касательную от участка а а’ к оси х. Касательная образует с осью х угол 0. В точках о и а" проводим линии, перпендикулярные к кривой. В некоторой точке О кривые пересекаются, образуя угол с/0. Это позволяет определить длину радиуса кривизны г. Так как длина участка линии обозначена как ds. получаем выражение ds — л7б или di)/ds — 1 /г. Вели прогиб б;ілкн небольшой (что справедливо для многих субстратов в реальных клеевых соединениях), то величина ds совпадает с величиной с/х Угол 0 имеет одинаковое значение с тангенсом 0 и тангенс 0 подобен отношению dy/dx. которое представляет собой просто мгновенный тангенс угла наклона кривой прогиба. Подставив эти приближенные значения в приведенные выше уравнения, получаем
1 _ с/0 1 d dy d dy _ d2y
r ds r ds dx dx dx dt! (2 63)
Отрицательный знак в данном выражении объясняется тем, что прогиб оказыва ется вогнутым вниз.
|
О
|
1‘ис 2 17. Схема, использованная для вывода уравнений прогиба балки Палка Л-А’ находится в состоянии чистого изгиба. Используя законы геометрии, п данном случае рассмотрена малая длина вдоль участка линии о а’ относительно осей х и у. показанных на схеме. (Схема перепечатана из работы Тимошенко с разрешения издательства Wadsworth hthlisking Со.)
К|Х>мс того, уравнение (2.63) может быть получено из выражения для определения кривизны, представленного ранее уравнением (2.52), при условии допущения, что прогиб балки чрезвычайно мал. Таким образом:
![]()
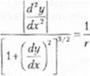 (2.6*)
(2.6*)
Если ирої иб имеет малую величину, то члену уравнения (dy/dx)2 соответствует очень малое значение и в атом случае можно утверждать, что
![]() 1 d2y
1 d2y
что аналогично полученному выше выражению
Подставив уравнение (2.62) в уравнение (2.65), получаем выражение
d’u
Е* (2 66)
Это лііс}м)н*рсііііііа.’іьиоо уравнение может быть проинтегрировано для определс — ння кривоіі щюгнба балки. подвершутой воздействию внешнего момента М. Это уравнение может быть дополнительно преобразовано с учетом уравнения (2.48). Взяв производную относительнох каждой части уравнения (2.66) и подставив уравнение (2.48), получаем выражение
![]() Е! ^- = — V U‘ dx * •
Е! ^- = — V U‘ dx * •
И наконец, можно взять другую производную этого уравнения (2.67) относительно. г к, принимая во внимание уравнение (2.50), получим:
![]() EI ^ = / ■dxl 1
EI ^ = / ■dxl 1
где / усилие на единицу площади при воздействии на балку равномерно распределенной нагрузки.
1* следующей главе будет показано как Голанд и Рейснер, а также Кейлбл исполь зевали эти основные уравнения для анализа механики двух типов клеевых соединений.
 6 сентября, 2015
6 сентября, 2015  admin
admin 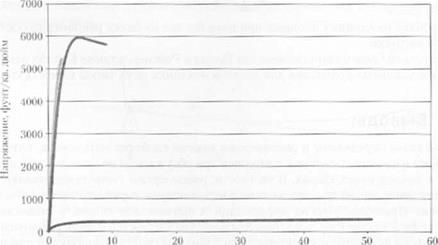
 Опубликовано в рубрике
Опубликовано в рубрике 