Состояние, которое для ряда веществ является промежуточным между кристаллическим твердым и изотропным жидким, называется жидкокристаллической фазой. Этой фазе присущи свойства как обычной жидкости (текучесть), так и твердого кристалла (например, двулучепреломление). Именно такое сочетание свойств привело к понятию жидкий кристалл, по сути внутренне противоречивому. Эквивалентными понятиями являются мезофаза (что означает промежуточная фаза), или мезоморфная фаза.
Чтобы понять природу жидкого кристалла, напомним, что происходит с обычным твердым кристаллом в точке плавления. В твердом кристалле центры масс молекул образуют трехмерную периодическую решетку, о чем свидетельствуют данные рентгено- структурного анализа (на рентгенограммах видны четкие брэг — говские рефлексы). В жидкости подобная трехмерная трансляционная симметрия (дальний порядок) пропадает и остается только некоторый ближний порядок в расположении центров масс молекул (в этом случае на рентгенограммах видны только диффузные Отражения, соответствующие такой структуре). Если молекулй вещества анизотропны, то в кристаллическом состоянии наряду с дальним порядком в расположении центров масс может существовать также и дальний порядок в ориентации молекул. Обычно оба типа упорядочения исчезают в точке плавления. Однако в случае жидких кристаллов это не так: хотя упорядоченность в расположении исчезает (или сильно уменьшается), но некоторая степень ориентационного упорядочения все же сохраняется. Молекулы таких кристаллов, как правило, сильно вытянуты, и их длинные оси параллельны друг другу, если не принимать во внимание тепловые флуктуации.
При нагреве до точки плавления твердое вещество, имеющее жидкокристаллическую фазу, переходит в довольно мутную жидкость. Помещенная между двумя скрещенными николями, такая жцдкость проявляет свойство сильного двулучепреломле — ния. При дальнейшем нагревании она становится изотропной и поэтому прозрачной. Температура, при которой это имеет место, называется точкой просветления. Точки плавления и просветления определяют интервал температур, в котором мезофаза термодинамически устойчива. Оба перехода (плавление и просветление) являются фазовыми переходами первого рода, на что указывает
существование скрытой теплоты перехода и скачкообразное изменение плотности. Однако в точке просветления и скрытая теплота, и изменение плотности на порядок величины меньше, чем в точке плавления.
Соединения, имеющие мезофазу, называются мезогенными. Заметим, что в дальнейшем понятие жидкий кристалл будет использоваться нами только применительно к мезогенному соединению в его жидкокристаллической фазе. Такие жидкие кристаллы, называемые термотропными, ведут себя как мезоморфные в определенном интервале температур и представляют собой одно — компонентные системы. Помимо термотропных существуют лио — тройные жидкокристаллические фазы, промежуточные между твердым состоянием и изотропным раствором. Лиотропные жидкие кристаллы не являются однокомпонентными системами, и их поведение зависит главным образом от количества растворителя.
|
ZNI |
В данной книге подробно рассматриваются свойства только термотропных кристаллов. Некоторые обзорные работы в об-
Таблица 1.1
Примеры нематических жидких кристаллов
Типы соединений
|
135,5 |
|
118 |
Л-азоксианизол, ПАА [4]
|
]Ч-(л-метоксибензилиден)-л-бутиланилин, МББА [103] 22 |
|
8 |
|
42 |
47
|
Fi-гексилокси-о-гидрокси-и’ — бутилазобензол [ 196] |
82
|
Л-гептил-п’-цианобифенил [63] |
28,5
Ласти жидких кристаллов приведены в начале библиографического списка. Среди них общий интерес представляет очерк Келкера по истории исследований жидких кристаллов.
Жидкие кристаллы можно разделить на нематические и смек — тические. Примеры нематических соединений приведены в габл. 1.1. Первое соединение п, гс’-диметоксиазоксибензол, или /г-азоксианизол (ПАА), — это «дрозофила» для исследователей
|
Рис. 1.1. Нематическая (а), хиральная нематическая (б) и смектическая А (в) фазы. Для простоты хиральная нематическая фаза изображена в случае Идеального упорядочения. X |
|
Б |
|
С |
Жидких кристаллов. Его точка плавления и температурная область существования нематической фазы типичны для многих давно известных мезогенных соединений. В качестве других примеров выбраны вещества, синтезированные относитель&о недавно и существующие в жидкокристаллической фазе при комнатной температуре (или несколько выше нее). Для нематической фазы (рис. 1.1, а) характерным является следующее:
— Длинные оси молекул в среднем параллельны друг другу, в результате чего образуется макроскопически выделенное направление, относительно которого имеется симметрия вращения, т. е. нематическая фаза одноосна;
— Дальний порядок в расположении центров молекул отсутствует, т. е. они могут свободно смещаться относительно друг друга, что свидетельствует о жидкостном характере нематической фазы и приводит, например, к появлению узких линий в спектрах ЯМР жидких кристаллов;
— Ось симметрии (вращения) фазы не обладает полярностью. (Заметим, что сами молекулы вещества могут быть полярными, но это не приводит к макроскопическому эффекту.)
Локальную ориентацию длинных осей молекул удобно описывать с помощью директора п — единичного вектора, указы
вающего преимущественную ориентацию длинных осей молекул в каждой точке жидкого кристалла. Последняя из перечисленных выше особенностей нематической фазы означает, что векторы п и —п эквивалентны (знак вектора не имеет физического смысла). Для конкретного образца жидкого кристалла положение вектора п определяется граничными условиями, а также внешними полями, используя которые можно получить однородную по кристаллу ориентацию директора (гл. 2, разд. 2). Если же специальные меры не приняты, то граничные условия вдоль границы подложки будут меняться, что приведет к неоднородной ориентации директора и, следовательно, к различному дву — лучепреломлению. В таких случаях при наблюдении под микроскопом тонкого слоя нематика, помещенного между скрещенными николями, появляется характерная картина — текстура. Сле-
Т*
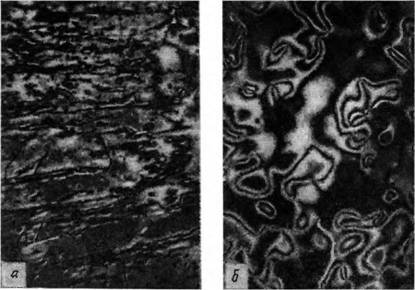
Дует заметить, что слово нематик (vrjiaa по-гречески означает нить) отражает основную особенность таких текстур: наличие нитей (рис. 1.2, а). Нити — это разрывы в картине расположения директора, которая обычно меняется на расстояниях, много больших, чем размеры молекул. На рис. 1.2, б показана шлирен-текстура, в которой нити (из нитей исходят темные полосы) перпендикулярны слою.
|
Рис. 1.2. Текстуры тонкого слоя нематика (скрещенные николп). А — текстура с нитями; б — голирен-текстура. |
Нематическая фаза может быть образована либо ансамблем одинаковых молекул, обладающих зеркальной симметрией, либо Рацемической (эквимолярной) смесью правой и левой форм оптически активных или энантиоморфных молекул. Если в смеси преобладает одна из форм, то образуется хиральная нематическая фаза (ее обозначают через N*). В таких случаях наряду с дальним ориентационным порядком в жидкости имеется пространственное изменение ориентации директора, приводящее к возникновению винтовой структуры (рис. 1.2, б). Ориентация длинных осей молекул в соседних плоскостях, перпендикулярных оси винта, отличается на небольшой угол. Винтовую структуру можно описать с помощью меняющегося в пространстве директора
71ж = со8<х, Пу = Sin ос, пг = 0 . (1.1)
Ось винта направлена вдоль оси Z, и а = Qoz + const. Директор совершает полный оборот на длине р = 2я/|до|, называемой Шагом. Знак величины до отличает правый и левый хиральные нематики. Поскольку директоры п и —п эквивалентны, период рассматриваемой структуры равен р/2. На практике величина р Может меняться от ~200 нм до бесконечности. Таким образом, величина р гораздо больше, чем размеры молекул. Это означает, что для молекул соседних плоскостей, церпендикулярных оси винта, различие в направлениях преимущественной ориентации чрезвычайно мало: локальный порядок, по сути, тот же, что и в нематиках. Примеры хиральных нематических кристаллов приведены в табл. 1.2. Поскольку к этому классу нематиков принадлежат многие производные холестерина, вместо названия хи — ральный нематик часто используется название холестерик. При сравнении нематической и хиральной нематической фаз обнаруживаются следующие важные факторы:
— Конкретное химическое соединение никогда не претерпевает фазового перехода из нематической в хиральную немати — ческую фазу;
— Два различных соединения, одно из которых имеет немати — ческую, а другое — хиральную нематическую фазу, могут дополнительно иметь при более низких температурах одну и ту же ^мектическую фазу;
— Обе фазы полностью смешиваются. Добавление малого количества оптически активного вещества (не важно, мезоморфное оно или нет) превращает нематик в хиральный нематик с большим шагом;
— Рентгенограммы нематической и хиральной нематической фаз очень похожи. В обоих случаях отсутствует дальний порядок в расположении молекул, который мог бы привести к Появлению четких рефлексов;
— Смесь двух веществ противоположной хиральности может
Образовать нематическую фазу: при определенной концентрации компонентов шаг винта становится бесконечным. В такой точке компенсации отсутствуют какие-либо аномалии физических свойств, которые могли бы указать на наличие фазового перехода.
Таким образом, можно сделать вывод, что хиральная нематическая фаза есть не что иное, как нематическая фаза, принимающая специфическую форму вследствие хиральности составляющих ее молекул. Другими словами, нематическую фазу можно рассматривать как хиральную нематическую фазу с бесконечным шагом. Если учесть сходство этих фаз, то название хиральный нематик является более предпочтительным, чем холестерик. Благодаря своей винтовой структуре хиральная нематическая фаза обладает уникальными оптическими свойствами [48].
Существует несколько видов мезофаз, называемых смекти — ческими. Обычно они обладают гораздо большей вязкостью, чем
Нематическая фаза (ац, т)7ца по-гречески означает мыло). Перечислим основные характеристики таких фаз:
— вытянутые молекулы ориентационно упорядочены, как в нематической фазе;
— В отличие от нематической фазы в расположении молекул имеется некоторый порядок: центры молекул в среднем расположены в эквидистантных плоскостях.
Прямое доказательство существования слоистой структуры дают рентгенограммы, на которых видны четкие рефлексы на малых брэгговских углах, соответствующих толщине слоев. Смектическая фаза простейшего типа (смектик А, или SA) изображена на рис. 1.1, в. Основные виды смектических фаз, которые наблюдались экспериментально, могут быть охарактеризованы следующим образом:
— Директор может быть параллелен нормали к слою или составлять с ней некоторый угол. В последнем случае, если в ориентации молекул имеется дальний порядок, смектическая фаза будет двухосной;
— В смектических слоях может дополнительно существовать упорядоченное расположение центров молекул.
Различные виды жидкокристаллических фаз, обладающих перечисленными особенностями, систематизированы в табл. 1.3. Соответствующие таким фазам рентгенограммы можно найти в работе [197], а фотографии и обсуждение различных текстур — в книге Демуса и Рихтера.
Таблица 1.3
|
Различные типы смектических фаз
|
В случае энантиоморфных молекул фазы с наклонным директором становятся хиральными смектическими фазами (Sc* и т. д.), при этом оси молекул слегка повернуты. Конкретные примеры веществ, обладающих смектическими фазами, даны в табл. 1.4.
Приведенные данные показывают, что мезогенные соединения могут иметь несколько различных мезофаз. Это явление называется полиморфизмом. В отличие от N1 и SI переходов в случае SN или SS переходов скрытая теплота может быть очень малой, и, по-видимому, эти переходы могут быть второго рода. Общепринятой классификации различных смектических фаз до сих пор не существует. В табл. 1.3 и 1.4 используются дбозначения, принятые в Галле, но в литературе символы G и Н иногда ме-
Няют местами. Сравнительно недавно были обнаружены мезо — фазы, состоящие из дискообразных молекул [231, плоскости которых параллельны друг другу. Мы ограничимся рассмотрением лишь одноосных фаз, преимущественно нематических.
В качестве примера рассмотрим нематическую фазу с однородной ориентацией директора. Выберем лабораторную систему координат таким образом, чтобы директор был направлен вдоль оси Z. Тогда направления х и у будут эквивалентными. Немати- ческая фаза обладает более низкой симметрией, т. е. она «более
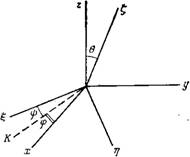
упорядочена», чем изотропная жидкость. Чтобы описывать подобное состояние количественно, введем представление о параМетре порядка, который отличен от нуля в нематической фазе и равен нулю в изотропной жидкости. Жидкость будем рассматривать как совокупность жестких молекул. Для описания ориентации молекул относительно лабораторной системы координат введем систему координат т], С, связанную с самой молекулой. Пусть ось £ направлена вдоль длинной оси молекулы. Тогда ориентацию осей молекулы полностью определяют три эйлеровых угла 0,г|э и ф(рис. 1.3, [136]): 0 — угол между осями z и ;; г|э — угол между осью £ и нормалью к плоскости (z, Q, описывающий поворот молекулы вокруг ее длинной оси, и (р — угол между осью х и нормалью к плоскости (z, С), описывающий поворот молекулы вокруг директора. Третий эйлеров угол ф в дальнейшем можно не учитывать, поскольку нематическая фаза обладает симметрией вращения. Степень
Ориентации молекул можно описать с помощью функции распределения м;(0, г|э) осей молекул по направлениям; величина м>(0, г|э) Mn0d0A|) есть доля молекул с эйлеровыми углами 0 и г|) в интервале между 0 и 0 + d0, i|) и + dip соответственно.
Для некоторой величины X среднее по ориентации всех молекул дается формулой
% 2к
|
(1.-2) |
(X) = jdQj dtyXw (0, i|>) sin 0 ,
Свойства нематической фазы таковы, что функция распределения W(Q, г|э), во-первых, должна слабо зависеть от величины угла г| а во-вторых, должна иметь резкие пики вблизи значений 0=0 И 0 = я (направление директора) и минимум при значении 0 =
Поскольку ориентации, соответствующие углам 0=0
И 0 = я, эквивалентны, то м;(0, г|э) = W(n — 0, г|)). Следовательно, если величина’ X в формуле (1.2) меняет знак при замене, 0 на я — 0, то ее среднее значение равно нулю.
|
Рис. 1.3. Молекулярная (S, rj, С) и лабораторная (я, у, Z) системы координат и углы Эйлера (К — нормаль к плоскости). |
На практике желательно иметь дело не с функцией распределения (ее трудно полностью определить), а с параметром по
рядка, который описывал бы степень ориентации длинных осей молекул вдоль директора. Можно было бы выбрать в качестве такого параметра величину С,, проекцию единичного вектора, направленного вдоль длинной оси молекулы, на направление директора. Поскольку, однако, среднее значение С2 =cos0 равно нулю, то в качестве параметра порядка S выбирают среднее значение величины £ 22 = cos2 9:
S = ± -1) = ± (3 cos* 8-1). (1.3)
Если длинные оси молекул распределены случайно, как в изотропной фазе, то (cos2 9) = 1/3 и S = 0. Значение *S=1 соответствует случаю идеальной ориентации молекул. На практике величина S может принимать значения от 0,3 — 0,4 при Т = = Tni До ~0,8 при значительно более низких температурах. Чтобы полностью описать среднюю ориентацию молекул, необходимо задать еще среднее значение либо величины £22 = = sin20 sin2i|), либо величины r2z = sin29 cos2^. Вместо этих средних удобно ввести величину [2]
D = -|- (чг-& = Y (sin28cos2i|>). (1.4)
Если величина D конечна (D Ф 0), то это свидетельствует о том, что проекции поперечных осей молекул на ось г различны. Однако это не означает, что нематическая фаза двухосная. Ни оси Н, ни оси г молекул не имеют ориентационного порядка.
В более общем виде можно описать ориентацию молекул не — матической фазы при помощи тензора параметра S с компонентами Sij, где I, F принимают значения т), С [36, 179]. Тензор S действительный, симметричный, его след равен нулю; таким образом, у него пять независимых компонент. Выше для упрощения рассмотрения нами была выбрана такая молекулярная система координат, в которой тензор S имеет только диагональные члены. На практике Ъто всегда осуществимо, и поэтому остается определить лишь две различные компоненты, в качестве которых выберем S = S^ и D = S^ — S&.
В случае необходимости анализа ориентации молекул реальных жидкокристаллических фаз прежде всего возникает проблема, как выбрать молекулярную систему координат. Обычно наиболее подходящим для привязки осей координат такой системы считают относительно жесткое ароматическое ядро молекулы. Для молекулы в транс-конфигурации (табл. 1.1, примеры 1—3) в качестве оси С часто выбирают ось, которая проходит через два крайних атома углерода, находящихся в иара-положении в ароматической части. Если бензольные кольца компланарпы (как, например, в азобензолах), то плоскость, в которой они лежат, выбирают в качестве плоскости (Н, С). Если компланарность отсутствует, можно выбрать плоскость, проходящую через ось С и составляющую равные углы с плоскостями бензольных колец. На практике различие между возможными вариантами выбора, по-видимому, невелико.
Следующая проблема обусловлена тем, что у мезогенных молекул обычно имеются гибкие группы, как, например, алкиль — ные цепи. Тогда в принципе можно было бы ввести параметр порядка для каждой СС-связи; из-за различий в гибкости эти параметры имели бы разные значения. Такие эффекты можно наблюдать с помощью спектроскопии ЯМР [49]. Рассмотрение этих вопросов выходит за рамки данной книги. Поэтому будем предполагать, что при описании «усредненной» конформации молекулы ее можно рассматривать как жесткую. Для описания реальных молекул часто используют следующие модели.
Модель жесткого стержня. Жесткие стержни, например вытянутые сфероиды, цилиндры, или сфероцилиндры (цилиндры с полусферами на концах), — это простейшие формы молекул, обладающих нематическими свойствами. Такие молекулы имеют цилиндрическую симметрию относительно оси С Хотя подобная симметрия отсутствует у большинства мезогенных молекул, тем не менее данная модель полезна, поскольку часто можно считать, что молекулы свободно вращаются вокруг оси С. В этом случае появляется цилиндрическая симметрия и функция распределения w(Q, г|)) не зависит от угла г|). В результате D = 0, и S остается единственным параметром для описания нематической фазы.
Молекулярно-статистическая теория, описывающая нематическую фазу с помощью одного параметра, получила развитие в работах [134, 135]. В приближении среднего поля предполагается, что каждая молекула испытывает воздействие среднего потенциала
Wi (0) = — (А IV2) S (± cos* е* — y) • (1.5)
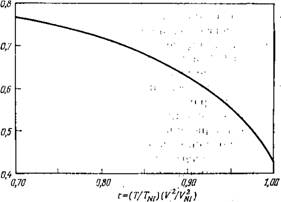
Где А — амплитуда потенциала, а V — молярный объем. Функция распределения связана с потенциалом соотношением и>(0) = = (1/Z)exp(—Wi/k& Т), где Z — нормировочная постоянная. В основе теории Майера — Заупе лежит рассмотрение взаимодействия между индуцированными диполями молекул. В этом случае амплитуда потенциала взаимодействия А приблизительно пропорциональна квадрату анизотропии поляризуемости молекул. Практически величина А рассматривается как эмпирический параметр, с помощью которого учитывают тацже и другие виды взаимодействия (например, отталкивание анизотропных молекул). Если Wi(Q) известно, можно вычислить разность свободных энергий нематической (конечное S) и изотропной (S = 0) фаз. При этом оказывается, что параметр порядка должен быть универсальной функцией приведенной температуры т =TV4{TmV2XI), причем при Т — Tm S =0,43 (рис. 1.4).
|
Рис. 1.4. Теоретическая зависимость параметра порядка S от приведенной Темпер ату рь^ ‘ |
В интересующей нас области температур его можно с точностью до 1% выразить аналитически; следующим образом:
5 = (1_0,98т)И:, . , . ‘ (1.6)
Хотя количественно предсказания Шёории ИЙайера — Заупе не точны, для многих жидких кристаллов они оказались хорошим приближением.
Модель твердого тела с двумя плоскостями симметрии. В качестве второй модели молекул рассмотрим анизотропное твердое тело, не обладающее осевой симметрией, но имеющее две взаимно перпендикулярные плоскости симметрии, линия пересечения которых образует ось С — Будем считать, что ось £ расположена в одной из плоскостей, а перпендикулярная ей оеь г) — в другой. Для наглядности можно представить себе удлиненйый эллипсоид с самой короткой осью в направлении г), или прямоугольный параллелепипед. Как и в предыдущей модели, для описания степени ориентации длинных осей молек’ул можно использовать величину S. Кроме того, величина D может оказаться не равной нулю, что будет характеризовать различие проекций двух поперечных осей молекулы на ось z. Величина Dможет быть не равной нулю, только если S Ф 1. Однако в предельном случае, когда S = 0 (т. е. когда нет дальнего ориентационйого порядка осей С), величина D также обязательно равна нулю. Следовательно, она ведет себя подобно
D~S(S — l). (1.7)
Авторы работы [126] обобщили теорию Майера — Заупе на случай молекул, не обладающих аксиальной симметрией. Максимум величины D в действительности достигался при S « 0,4. Поскольку это примерно равно значению S при Т == Гш, можно ожидать, что с понижением температуры величина D Уменьшается. Конечно, все это имеет место только в том случае, когда отсутствует свободное вращение молекул вокруг оси С.
В заключение заметим, что при обсуждении степени порядка предполагалось, что поле директора однородно вдоль оси Z. В реальном жидком кристалле, если не принять специальных мер, это будет не так. Однако вектор п существенно меняет направление только на расстояниях, много больших, чем размеры молекул, и можно считать нематик локально одноосным. Тензор S описывает при этом среднюю степень порядка относительно локального директора. Иными словами, пространственное изменение вектора п и температурную зависимость параметра порядка S можно рассматривать отдельно. Эта возможность лежит в основе континуальной теории жидких кристаллов, которая обсуждается в гл. 6 и 7. До этого момента можно считать, что поле директора в жидком кристалле одпородно.
 16 января, 2013
16 января, 2013  admin
admin 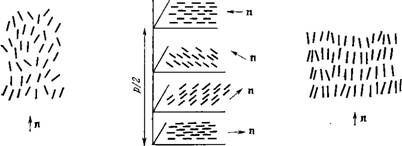
 Опубликовано в рубрике
Опубликовано в рубрике 