Особенностью оптических свойств одноосного жидкого кристалла является наличие у него двух главных показателей преломления. Один из них п0 характеризует распространение обыкновенной световой волны, электрический вектор которой перпендикулярен оптической оси, другой пе — распространение необыкновенной линейно-поляризованной световой волны, электрический вектор которой параллелен оптической оси.
У нематического и одноосного смектического кристаллов оптическая ось совпадает с направлением директора. Используя ранее введенные обозначения для направлений, параллельного ( || ) и перпендикулярного (j_) директору, имеем
П0=пг (4.1, а)
Пе = пу (4.1, б)
Величина двулучепреломления характеризуется разностью
An = пе — п0 = — п± . (4.2)
Так как на практике обычно П\>п^_у то нематический кристалл обладает положительным двулучепреломлением (An > 0; рис. 4.1, а). Величина An меняется от значений, близких к нулю, до ~0,4.
Для хирального нематического жидкого кристалла равенство (4.1, а) не выполняется. В этом случае единственная оптическая ось совпадает с осью винта, перпендикулярной локальному направлению директора. Если длина световой волны значительно больше шага винта, то
= (П +7ii)T/2 ,
(4.3)
Пе = п±.
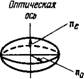
Поскольку, как правило, пц >п±, хиральные нематики обладают отрицательным двулучепреломлением (Ап< 0; рис. 4.1, б)
Формально можно говорить о том, что показатель преломления отражает реакцию вещества на электрическое поле. В образце, помещенном в поле наводится электрическая поляри
зация Р, связанная с величиной Е и диэлектрическим смещением D соотношением
P = D—e0E, (4.4)
|
|
Где е0 — диэлектрическая проницаемость вакуума. Поляризация JP в малых полях пропорциональна Е. Для любой анизотропной среды, и в частности для одноосных жидких кристаллов,
|
|
Рис. 4.1. Эллипсоид поляризуемости для положительной (я) и отрицательной (б) одноосных сред.
Справедливо соотношение, аналогичное соотношению (3.3) для магнитного поля:
Р* = еоХЛр£?. а» Р У. (4.5)
Где х^э — компонента тензора диэлектрической восприимчивости Yf. При описании диэлектриков часто используют величину относительной диэлектрической проницаемости, связанную с восприимчивостью соотношением
Где 1 — единичный тензор. Вообще говоря, е зависит от частоты внешнего электрического поля. В этой главе мы рассмотрим область оптических частот, в которой
(па — показатель преломления для направления а). Уравнения (4.5—4.7) дают феноменологическое описание связи между показателем преломления и электрической поляризуемостью. По — прежнему считая, что ось Z совпадает с направлением директора,
Получаем п\ = пг и п± = (nl + п2у)]Ч*.
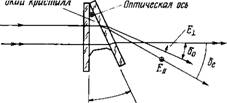
Измерение показателей преломления жидкого кристалла удобно проводить методом двойной призмы Аббе, согласно которому жидкий кристалл в виде тонкой пленки помещается между гипотенузными гранями двух призм. Если показатель преломления призмы больше, чем показатели преломления жидкого кристалла, то можно измерить предельные углы, соответствующие полному отражению как обыкновенной, так и необыкновен
ной световой волны (рис. 4.2). Предельный угол, связанный с п0, Можно определить с большей точностью, если при помощи поляризатора устранить необыкновенную волну. Практически для этого оказывается достаточно использовать промышленные рефрактометры, обеспечивающие возможность непосредственного отсчета по. Обычно имеет место соотношение по<С п<С пе, и значение пе определить нельзя, если не использовать специальные призмы (где п показатель преломления призмы). Однако вместо измерения величины пе интерференционным методом можно непосредственно измерять разность An.
|
Жг* г
Рис. 4.2. Угол полного отражения обыкновенного и необыкновенного лучей в клиновидном образце. |
Для определения величины An можно использовать однородный пленарный образец, который устанавливают таким образом, чтобы его оптическая ось составляла угол в 45° с плоскостями скрещенных поляризаторов. Свет, падающий перпендикулярно плоскости образца, расщепляется на обыковеиный и необыкновенный лучи равной интенсивности. После прохождения образца два луча, фазы которых становятся разными, интерферируют в анализаторе. Интенсивность прошедшего света записывается с помощью фотодетектора. Если X — длина волны (монохроматического) света, a D — толщина образца, интенсивность минимальна, тогда
DAn =-.= кк,
Где к — целое число. Используя уравнение (4.8), можно определить An различными способами.
|
(4.8) |
]-й способ. При фиксированных значениях D и X можно записать интенсивность прошедшего света как функцию температуры в процессе ее непрерывного изменения и получить температурную зависимость Ап(Т). Поскольку An в точке просветления меняется скачком и, следовательно, значение к, соответствующее первому минимуму интенсивности света, при температуре ниже ТNi неизвестно, то для определения абсолютной величины An необходимо еще одно независимое измерение.
2- Й способ. При фиксированных значениях X и Т можно использовать клиновидный образец [72], у которого толщина D меняется вдоль оси х от нуля до значения Do. Если толщина равна Do на расстоянии хо от вершины клина, то толщина в точке х определяется выражением D — Xdolxo. В этом случае появляется ряд равноотстоящих интерференционных полос, расстояние Ах Между которыми можно измерить. Поскольку для соседних полос величина к отличается на ±1, находим
An = Xx0/(Axd0) . (4.9)
Достоинство 2-го способа состоит в том, что с его помощью можно найти абсолютное значение An. Однако необходимые для этого измерения более сложны, чем при 1-м способе, и их приходится повторять при всех интересующих исследователя температурах.
3- Й способ. При фиксированных значениях D и Т можно мет нять длину волны. !Ёсли при некотором значении к минимум интенсивности прошедшего света наблюдается при длине волны Xi, то при уменьшении длины волны следующий минимум возникнет при (А; 4- 1)Хг. Таким способом можно найти относитель?* ное изменение An с длиной волны, а для определения абсолют-* ной величины An нужно знать значение /с, поэтому и в этом случае, как и при 1-м способе, необходимо еще одно независимое измерение А п.
В целом 1-й способ, основанный на использовании лучей света с различивши длинами волн, по-видимому, является простейшим для получения полной информации о An. Что касается абсолютного значения А/г, то его можно определить следующим образом. Временно пренебрегая тем фактом, что зависимость Ап'(Т) в точке TNi имеет разрыв, экстраполируем значение Anis для изотропной жидкости в область более низких температур и найдем приближенное значение п -1- 2ri±).
Зная п и п±, можно приближенно оценить величину An. Для тонкого образца при к ~ 5 точность этой процедуры вполне достаточна, чтобы однозначно определить к, а затем An [118]. Вместе с тем следует иметь в виду, что 2-й способ позволяет сразу получать абсолютное значение An.
Наконец, отметим, . что интерференционную технику можно использовать и иным образом. Если отражающей сделать поверхность подложки, более удаленной от источника света, и частично отражающей — поверхность подложки, более близкой к источнику, то можно наблюдать, интерференцию света, отраженного от этих двух поверхностей. Для планарного образца можно, например изменяя направление поляризации падающего луча, определить зависимость показателей преломления п\ или п}
|
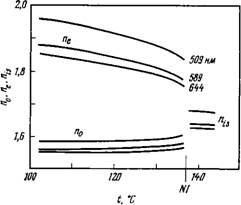
Рис. 4.3. Показатели преломления ПАА для различных длин волн [25]. |
От температуры или давления. Вообще говоря, предпочтительнее измерять непосредственно величину Дп, однако для измерений при высоких давлениях этот метод оказывается полезным [83].
|
|
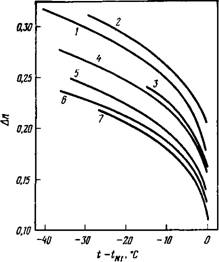
Некоторые результаты измерений показателей преломления ПАА для различных длин волн приведены на рис. 4.3. Дисперсия обоих показателей преломления в нематической фазе оказывается нормальной (л возрастает с ростом X), но для п л она много больше, чем для гг1. На рис. 4.4 приведены некоторые результаты измерения An для ряда п, тг’-диалкоксиазоксибензолов. В этом гомологическом ряду наблюдается знакопеременное изменение An, которое имеет место одновременно с хорошо известным изменением TNi— К настоящему времени опубликованы Рис. 4.4. Двулучепреломление для чле — многочисленные результаты Нов ряда л, п’-диалкоксиазокснбензо- измерений показателей прелое при длине волны 663 нм 1/4]. (Циф — ^ г ры на кривых соответствуют числу ато- ломления следующих нема — Мов углерода в цепи.) тиков: азоксибензолов [25,
74, 90], алкоксибензойных кислот [176], толанов [113], шиффо — вых оснований [20, 160], цианобифенилов [82], фенилбензоатов [160, 186] и эфиров холестерина [162][2].
Когда в однородное электрическое поле небольшой напряженности Е помещается некоторое тело, в нем наводится дипольный электрический момент ш, компоненты которого линейно зависят от Е [171:
M = <%•£, (4.10)
Где а — тензор поляризуемости этого тела. Рассмотрим в качестве важного примера модель — тело сфероидальной формы с главными осями 2а и 2Ь и проницаемостью е в вакууме. Если выбрать ось z вдоль длинной оси 2а вытянутого сфероида, то тензор л примет диагональную форму и его компоненты будут равны[3]
Ат=е0(е -1)[1 + (е — 1) Й F11 ± ъаЪ у = а, Ь. (4.11)
Факторы формы или коэффициенты деполяризации зависят только от отношения полуосей alb и равны
£2а = 1 — w2 + — w (w2 — 1) In (w + 1 )l(w — 1)],
(4.12)
Ab = ±(i-aa)f
Где ш2 г— a2i(a2 — б2). В частном случае, когда сфероид переходит в шар (а = 6), Qa = = */з, уравнение (4.11) сводится к уравнению для скалярной поляризуемости. В общем же случае молекулу характеризует тензор поляризуемости а. Наведенная поляризация складывается из двух частей, так как электрическое поле вызывает смещение электронов относительно ядер в каждом атоме (электронная поляризация) и смещение одних ядер относительно друГйх (ионная поляризация). В органических жидкостях второй вклад обычно составляет лишь 5—10% от электронной поляризации. Кроме того, ионная поляризация существенна вплоть до частот ИК-области и, как правило, несущественна в видимой части спектра. Поэтому будем считать, что показатель преломления и тензор диэлектрической проницаемости е в оптической области частот связаны только с электронной поляризуемостью молекул л. Для изотропной фазы, используя выражение (4.10), находим
P=N*Eiy (4.13)
Где N — число молекул в единице объема, A Et— внутреннее, поле, т> е. среднее поле, действующее на молекулу. Величина. Ei равна сумме макроскопического внешнего поля Е и сред-: него поля, создаваемого наведенными моментами окружающих молекул. Расчет Ei представляет собой одну из главных проб лем в теории электрической поляризации. Для облегчения расчетов обычно используют два метода, основанные на различных приближениях [17]. В первом методе для нахождения электрического поля, действующего на отдельную молекулу, считают[4]Окружающую ее среду макроскопическим континуумом со свойствами рассматриваемого диэлектрика. Это довольно грубое допущение приводит к серьезным трудностям, которые связаны с возможностью применения результатов, найденных для макроскопических тел, к частицам молекулярных размеров. Во вто^ ром методе явно учитывается взаимодействие молекул и для вычисления Ei используются приемы статистической механики. Хотя такое приближение a priori можно считать более приемлемым, расчет удается выполнить только после значительных упрощений. Поэтому будем рассматривать в основном первое приближение.
В случае жидкого кристалла уравнение (4.13) можно обобщить следующим образом:
Р £,), (4.14:)
Где скобки означают среднее по ориентациям всех молекул. Поскольку внутреннее поле есть линейная функция макроскопического поля, они связаны соотношением
Et = К — (4.15)
Где К — обычный тензор второго ранга. Тогда уравнение (4.14) можно записать в виде
P = N(*.K)E. (4.16)
В то же время уравнения (4.5) и (4.6) связывают 1* с макроскопической относительной проницаемостью1 е:
T = 1 + (ЛГ/е0) <* • К> . (4.17)
Поэтому анизотропия диэлектрической проницаемости
Де = п-п = (N/S0) (<« • К), — (« • К)х). (4.18)
Чтобы воспользоваться уравнениями (4.17) и (4.18), нужно знать тензор К» характеризующий внутреннее поле Ei- В общем случае можно считать, что тензор К зависит как от свойств и ориентации молекулы, на которую действует внутреннее поле, так и от тензора диэлектрической проницаемости макроскопического образца. Если учесть все эти зависимости, то получаются очень Сложные выражения" [112]. Чтобы упростить задачу о нахождении внутреннего поля, используем некоторые экспериментальные данные.
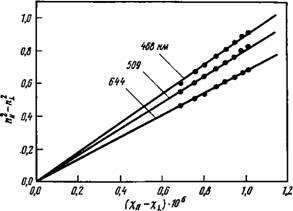
Исследования проницаемости в области оптических частот позволили Установить два важных факта [90]. Во-первых, отношение е/р средней проницаемости 8 У (ец + к плотности для данного вещества не меняется при переходе между изотропной и нематической фазой. Во-вторых, анизотропия диэлектрической проницаемости прямо пропорциональна анизотропии магнитной восприимчивости. Пример такой зависимости приведен на рис. 4.5 для МББА при различных длинах волн. Для аксиально-симметричных молекул величина пропорциональна параметру порядка S [уравнение (3.21)], так что, используя равенство находим
Де =71*—п2_ (4.19)
В уравнении (4.18) плотность частиц представлена величиной N — NAp/M, где Na — число Авогадро, а М — молекулярный вес. Поэтому сравнение уравнений (4.18) и (4.19) приводит к условию для тензора внутреннего поля
(4.20)
Если предположить, что молекулы аксиально-симметричны относительно оси то тензор электронной поляризуемости будет диагональным в той же системе координат S, т|, ч, в которой диа — гонален тензор магнитной восприимчивости. Тогда главными
Компонентами тензора будут At = и at = ат4т(),
И аналогично уравнениям (3.19) и (3.21) находим
, (а)|-(а)1=(а/-а T)S. (4.21)
Чтобы выражения (4.20) и (4.21) удовлетворялись одновременно, тензор К» характеризующий внутреннее поле, создаваемое всеми молекулами кроме данной, не должен зависеть от диэлектрической анизотропии макроскопического образца и, следовательно, от ориентации молекулы относительно преимущественного Направления директора. Поэтому главные оси а и К должны
Совпадать. Тогда аналогично формулам (3.19) получим из выражения (4.17)
Е и = I»2 = 1 + (N/Зе0) [а 1К1 (2S + 1) + аTKt (2 — 25)],
Е± = П = 1 + (N/Зе0) [аLKl (1 —S)+ аTKt (2 + S)], (4.22)
Где К I и К T — главные значения К — Мы приходим к выводу, что учесть внутреннее поле можно, если ввести тензор эффективной поляризуемости а* Этот вывод важен для некоторых
|
2 2 Рис. 4.5. Зависимость, существующая между величинами пц —л^ [20] и Л% [93], для соединений типа МББА. |
Практических применений, например при исследовании комбинационного рассеяния [86]. Ближайшие соседи почти полностью определяют поле, обусловленное индуцированными моментами молекул,- поскольку диполь-дипольное взаимодействие падает, как г"3. Взаимодействие ближайших соседей слабо зависит от температуры в большинстве конденсированных фаз и, вероятно, не меняется существенно даже при различных фазовых переходах. Это, вероятно, й есть причина того, что К можно считать молекулярным тензором.
Используя пропорциональность, описываемую уравнением
(4.19), и учитывая постоянство величины е/р, получаем
An~pftS. (4.23)
Поскольку изменение плотности в температурной области существования нематика обычно очень мало, соотношение (4.23) означает, что относительно простые измерения температурной
Зависимости An дают возможность найти изменение S с температурой Т. Следует, однако, иметь в виду, что точность определения зависимости S(T) не обязательно совпадает с точностью измерения величины An и тем выше, чем выше точность выполнения условия пропорциональности Де ~ Д%.
Если необходимо вычислить молекулярные электронные поляризуемости а / и а Ty то нужно обратиться к модели для тензора К. Чтобы получить разумные значения для К I и К T в уравнении (4.22), рассмотрим случай идеального упорядочений 5 = 1. Пря этом ец и будут примерно равны соответствующим величинам для твердых тел, если все молекулы в твердом теле имеют одинаковую ориентацию. Вукс [198] предположил, что внутреннее поле в твердом теле с симметрией, более низкой, чем кубическая, не зависит от ориентации и равно
£«=-±-(1 + 2)£. (4.24)
Это означает, что тензор К изотропен. Подстановка в уравнение (4.22) дает [22]
( е -1 )/(7 + 2) = (N19е0) [a, (2S + 1)+ а, (2 — 25)],
(4.25)
( -1)/( е + 2) = (N19е0) {а, (1 -S) + а, (2 f S).
Данные уравнения можно использовать для вычисления средней поляризуемости а I + 2а t):
А = (Зе0/АГ) (7 — 1)/(7 + 2) . (4.26)
Мы получили формулу Лоренц—Лоренца, которую обычно выводят для изотропных фаз или систем с кубической симметрией, где е = е. В подобных случаях внутреннее поле, определяемое уравнением (4.24), называют полем Лоренца. Таким образом, приближение Вукса приводит к формуле для изотропной фазы, совпадающей с формулой Лоренц—Лоренца.
Тем не менее уравнение (4.25) вызывает ряд возражений. Во-первых, у него нет молекулярного обоснования даже для случая твердых тел, гораздо более простого, чем случай жидких кристаллов. Во-вторых, нередко приближение Вукса дает неправдоподобные результаты. Для ПАА, например, как /гц, так и nL обладают нормальной дисперсией, значительно более сильной для п и, чем для (рис. 4.3). Если же вычислить a t из уравнений (4.25), то эта величина будет обладать аномальной дисперсией, что бесспорно является следствием неточности этих уравнений. Далее, у кристалла йодоформа показатель преломления вдоль оси третьего порядка молекулы больше, чем показатель преломления, перпендикулярный этой оси. Уравнение Вукса в этом случае даст положительную анизотропию поляризуемости, тогда как измерения эффекта Керра в растворе показывают, что эта анизотропия отрицательна.
При выводе — уравнений Лоренц—Лоренца молекулу считают точечным поляризующимся объектом в сферической полости. Более точным представлением реальной молекулы был бы анизотропный однородно поляризующийся сфероид, заполняющий полость в анизотропном поляризующемся континууме. Для одноосного твердого кристалла при этом получаем [18]
«7 = (Ч/N) ( S7 —1)/[1 + ( ет — 1) О ], у = I, T, (4.27)
Где QT — коэффициенты деполяризации, зависящие только от отношения осей сфероида. Они равны коэффициентам деполяризации в электростатической задаче о диэлектрическом сфероиде, находящемся во внешнем поле [см. уравнение (4.12)]. Соответствующее внутреннее поле можно записать так:
(£,)т = [1 + ( ^ -1) Й ] Е1 = е0 (£0 — ЛГ. Д)-‘ Е7. (4.28)
Если не принимать во внимание слабую зависимость (2£г)т от плотности, то это уравнение удовлетворяет требованию о независимости внутреннего поля от макроскопической диэлектрической анизотропии. После соответствующих подстановок [ш. выражения (4.15) и (4.28)] равенства (4.22) дают
S„ N «f(2S + P , M2-2S)-]
11 3 L
(4.29)
S I 1 yf A,(2 + S). I
1 3 ‘ I E0 — Nafit e0 — ‘
Эти формулы позволяют находить а г и а * по экспериментальным значениям 8ц и Е±, если известны плотность и параметр порядка. Результат зависит от отношения alb. В табл. 4.1 приведены значения поляризуемости ПАА и п, тг’-дигептилазобен — зола, найденные по модели сфероида. Более ранние результаты получены с помощью данных о показателях преломления твердого ПАА [24] и вычислений на основе уравнений (4.27). В более поздних расчетах использовались значения показателей преломления нематической фазы и уравнения (4.29) [98]. Длинная ось сфероида считалась равной длине полностью вытянутой молекулы и находилась из молекулярной модели. Ширина выбиралась так, чтобы объем сфероида был равен объему, приходя — птемуся на молекулу, при Т — Гмь
Уравнения (4.29) остаются справедливыми в интервале между S = 0 и S = 1. При S ~ 0 результат несколько отличается от формулы Лоренц—Лоренца, но для изотропной жидкой фазы, состоящей из анизотропных молекул, например для сероуглерода CS2, он лучше согласуется с экспериментом [90]. При S = 1 формулы (4.29), конечно, сводятся к исходному уравнению (4.27) для твердого тела. Напомним, что уравнение (4.29) основано не на молекулярной модели диэлектрической проницаемости нематической фазы в оптическом диапазоне длин волн, а на экспериментальных фактах: неизменности е/р для твердой и жидкокристаллической фаз и линейной зависимости Де ~pS. Формула Вукса (4.24) для внутреннего поля эквивалентна уравнению (4.28) при
AT = Y(7_1)/(eT-1)e Т= н, _ь (4.зо)
Если наибольшее значение ет соответствует длинной оси молекулы, для которой QT <1/3, то это равенство приближенно верно. Если же наибольшее значение ет соответствует короткой оси молекулы (как в примере с йодоформом), формула Вукса может привести даже к неверному знаку анизотропии поляризуемости.
Наконец, упомянем об обобщении Нейгебауэром лоренцев — ских вычислений внутреннего поля на случай кубического кристалла [152]. Была рассмотрена произвольная решетка анизотропных молекул, которые считались поляризующимися точечными объектами с параллельными главными осями. Было получено уравнение, аналогичное (4.27), с коэффициентами QT, которые имели иной смысл и зависели от структуры кристалла. Это различие обусловлено тем, что поле однородно поляризованного сфероида не равно полю поляризующейся точки в сфероидальной полости [17].
Представление о молекуле, как о точке с анизотропной поляризуемостью, очень ограничено, так как в действительности поляризуемость молекулы распределена по объему. Учет этого обстоятельства не играет роли в случае сферических или почти сферических частиц, однако с ростом анизотропии формы такой учет становится все более необходимым. Более того, если формулу Нейгебауэра пытаться применять к нематикам, становится неясным, как определять в этом случае решетку. Эту трудность можно обойти искусственным путем, выбирая QT таким образом, чтобы а в нематической или твердой фазе было равно значению, полученному для изотропной фазы с помощью формулы Лоренц— Лоренца [181]. Поскольку подобная процедура представляется неудовлетворительной, мы не приводим результатов для а г и A,f, полученных таким способом.
|
Таблица 4.1 Электронные поляризуемости двух нематических соединений (10"40 Фм2)
|
|
1 Экстраполированные значения. |
Чтобы проверить результаты для молекулярных электронных поляризуемостей, приведенных в табл. 4.1, нужно получить значения а; и др»угим независимым методом. В принципе такие результаты могут быть найдены из измерений постоянной Керра. Однако интерпретация таких измерений как для изотропной фазы, так и для разбавленных растворов в той же степени связана с проблемой внутреннего поля, что и интерпретация измерений показателей преломления (см., например, [18]). Поэтому результаты, получаемые различными методами, согласуются с любым выражением для внутреннего поля, соответствующим соотношению (4.20), и такое согласие еще не доказывает, что теоретическое рассмотрение внутреннего поля проведено корректно. Для проверки нужен метод, в котором отсутствовала бы проблема учета внутреннего поля. Это возможно только в случае вещества, находящегося в газообразном состоянии, однако для соединений, имеющих жидкокристаллическую фазу, нельзя создать высокую плотность паров при температурах, при которых можно избежать разложения, т. е. при достаточно низких температурах.
В такой ситуации лучше всего проверить, совпадают ли результаты, получаемые различными методами. С этой целью наряду с показателями преломления и постоянной Керра целесообразно с помощью оптической спектроскопии измерить ди — хроичное отношение R. Для жидкого кристалла величина R определяется как частное от деления поглощения, измеренного при распространении света параллельно направлению директора, на поглощение, измеренное в перпендикулярном направлении. Чтобы связать это отношение с величиной Дшоь представляющей поглощение при распространении света вдоль оси молекулы, деленное на поглощение при распространении света поперек оси, можно воспользоваться формулой [181]
Ято. =(п|1/п1)[(£г)1/(£:/)||)]2Д. (4.31)
Блинов и др. [12] изучали поглощение света некоторыми молекулами-зондами, структура которых подобна структуре молекул нематика, который использовался в качестве растворителя. Отношение Лц/л^ возрастает с уменьшением длины волны. Если использовать теорию Нейгебауэра, это возрастание должно приводить к некоторому увеличению R с уменьшением длины волны. Напротив, модель изотропного внутреннего поля [формула Вукса, уравнение (4.25)] и сферическая модель [уравнение (4.49)] приводят к снижению величины R при уменьшении длины волны. Этот результат и согласуется с наблюдаемой экспериментальной зависимостью величины R от длины волны.
Были выполнены также эксперименты с использованием шаровых молекул-зондов, для которых -ffmoi =1- В этом случае величина R оказалась меньше единицы и в пределах точности эксперимента равной отношению Njn\. Следовательно, в этом частном случае изотропных молекул, находящихся в не — матическом растворителе, внутреннее поле изотропно. На этом основании можно сделать вывод, что любая анизотропия внутреннего поля в нематической фазе должна быть связана с анизотропией исследуемых молекул. С учетом критических замечаний, относящихся к формуле Вукса, это обстоятельство свидетельствует в пользу сфероидальной модели.
Разумные оценки электронных поляризуемостей молекул часто можно получить, складывая известные табличные значения поляризуемостей связей [121]. К сожалению, этот метод не очень хорош в случае сопряженных систем, где значение поляризуемости может оказаться гораздо больше, чем значение, полученное в результате такого суммирования. Например, используя поляризуемости бензола и группы —N=N—, можно найти для азобензола [98]
А/ = 28, At = 21 (Ю-40 Ф • м2).
Из измерений постоянной Керра для азобензола было найдено
А, = 38, а, = 22 (10"40 Ф-м2).
Если не учитывать возможную неопределенность интерпретации, очевидно, что сопряжение в продольном направлении приводит К сильному увеличению az. Из поляризуемостей связей С—С И С—Н можно найти для алькильной цепи в плоской сплошной Транс-зигзаг-Конформации величину возрастания At и At После добавления метильной группы. Полученные таким образом данные представлены в табл. 4.2. Из приведенных выше оценок величин at и at для азобензола и этих данных находим для п, п’- Дигептилазобензола
Az = 70, <xt = 49 (10"4° Ф-м2).
Этот результат для а, несколько меньше, чем значения, полученные на основе сфероидальной модели (табл. 4.1). Такое расхождение может быть в основном связано с неопределенностью в интерпретации эффекта Керра. Вместе с тем возможно также, что анизотропия молекулы, определенная при оценке отношения осей alb, Оказалась несколько завышенной.
|
Таблица 4.2 Инкременты продольной и поперечной поляризуемостей для алышльной группы в планарной зигзаг-конфигурации (Ю-40 Ф м2)
|
Из данных, приведенных в табл. 4.2, видно, что добавление метильной группы к цепи с четным числом атомов приводит к увеличению разности At — at, в то время как в случае цепи с нечетным числом атомов следует ожидать небольшого уменьшения указанной разности. Это обстоятельство качественно объясняет осцилляцию величины An, часто наблюдаемую при увеличении длины цепи в гомологическом ряду (рис. 4.4). Такая осцилляция происходит одновременно с известной осцилляцией величины JNi— ЕСли нематическое поведение вещества определяется анизотропией дисперсионных сил [уравнение (1.4)], то можно ожидать пропорциональности величин TNi И (al — at)2. Однако, вообще говоря, в определение величины JTNi Вносят Вклад и другие эффекты. В табл. 4.3 проведено сравнение некоторых результатов измерения величин An и Тм для различных веществ. Если предположить, что при температуре (JNi — Ю)° С плотность и параметр порядка сравниваемых веществ различаются несильно, то величину az — at можно приближенно характеризовать величиной An. Примеры 1—3 Показывают, что когда алкокси-группа замещается алькильной группой, величины An и ТNi падают. Этого и следовало ожидать, поскольку у атомов кислорода имеется несвязывающая (неподеленная) электронная пара, которая легко включается
В систему сопряженных связей. Падение величины At (а поэтому и разности at — at) при замене кислорода на СШ-группу в этом случае сопровождается уменьшением TNi— Фенилбензоаты (№ 5, табл. 4.3) обладают гораздо менее жесткой мостиковой группой, чем другие приведенные в качестве примера вещества, и это приводит к относительно небольшому взаимодействию, связанному с сопряжением. Соответственно величина Дп в таких случаях также меньше, однако величина TNi еще относительно велика. Наконец, в примерах 6—8 бензольные кольца (поляризующиеся вследствие делокализации я-электронов в основном в плоскости кольца) замещены гораздо слабее поляризующимися циклогексановыми кольцами. Как и следует ожидать, двулучепреломление в таких веществах резко падает. Тем не менее для них наблюдается некоторое увеличение Гмь Поэтому можно сделать вывод, что иногда наблюдаемая качественная пропорциональность между TNi И (at — at)2 [100], вообще говоря, не имеет места и, вероятно, справедлива только в тех случаях, когда рассматриваемые изменения молекулярной структуры относительно невелики. Тогда такие величины, как полная поляризуемость, анизотропный объем, которые наряду с at — а могут оказывать влияние на величину Тмь не должны изменяться существенно.
 18 января, 2013
18 января, 2013  admin
admin 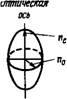
 Опубликовано в рубрике
Опубликовано в рубрике 