К числу физических свойств жидкого кристалла, которые являются анизотропными, принадлежит магнитная восприимчивость.
В системе единиц СИ намагниченность магнетика выражается через магнитную индукцию В и напряженность внешнего магнитного поля Н с помощью соотношения
TOC o "1-3" h z М=ро1В — Н, (3.1)
Где |л0 — проницаемость вакуума. Разделив обе части уравнения на Jj—O^JB, получим безразмерную величину — магнитную восприимчивость1
В случае анизотропных фаз скалярную величину % следует заменить тензором второго ранга и записать уравнение (3.2) в более общем виде:
Ma = МQlXapBt>> <*> Р (3-3)
где — компоненты тензора, а х, у, Z — оси координат. Ограничим наше рассмотрение одноосными фазами, к которым относится нематическая фаза, и будем считать, что директор п направлен вдоль оси Z. В этом случае тензор % имеет диагональную форму:
|
|
Индексы || и _L относятся к компонентам восприимчивости, направленным параллельно и перпендикулярно директору соответственно. Средняя восприимчивость одноосной фазы может быть представлена в виде
X =
О Ввиду малости величины х для жидких кристаллов автор в дальнейшем всюду учитывает различие между В и Н только в первом порядке по X, пренебрегая членами второго и высших порядков. — Прим. ред.
А анизотропия магнитной восприимчивости — в виде
Дх = Хц— = ( Xн х) • (3.5)
Поскольку в рассматриваемом случае тензор магнитной восприимчивости имеет лишь две отличные от нуля компоненты, получаем следующие выражения для намагниченности:
^F = Цо^Х Ц By если В || п,
(3.6)
М = |Ло V. J. В, если В JL П.
Для произвольного угла между векторами В и п полная намагниченность
М = Но-1 /±В + ц-^х (В • п) п, (3.7)
И изменение свободной энергии, обусловленное магнитным полем, равно [68]
Лпа8п= (3.8)
Восприимчивость определяется намагниченностью, т. е. магнитным моментом единицы объема образца, и поэтому величина так же как и намагниченность, относится к единице объема вещества (объемная восприимчивость), A /^magn в выражении (3.8) представляет собой плотность магнитной энергии. Наряду с объемной можно использовать массовую восприимчивость %т, т. е. восприимчивость единицы массы вещества. Для образца массой Т и объемом V имеем %тт = %V, или, вводя плотность р,
Ут = у/р [м3• кг-*| . (3.9)
Молярная восприимчивость %м относится к одному молю вещества
УМ = ХтМ [щЗ. моль-[1]]. (3.10)
Где М — молекулярный вес.
Подобно большинству органических веществ, жидкие кристаллы, как правило, являются диамагнетиками. Это означает, что величины х || и Yvl отрицательны и малы (порядка 10~5 ед. СИ)1. В большинстве случаев разность А% имеет положительное значение. Поскольку диамагнитная восприимчивость не зависит от температуры, %т нематической фазы равно изотропной восприимчивости %т, измеренной выше температуры rNI. Помимо диамагнитных жидких кристаллов известно также несколько парамагнитных мезоморфных свободных радикалов, синтезированных в последнее время [44].
Для измерения магнитной восприимчивости обычно используется классический метод Фарадея — Кюри. Образец объемом V помещается в сильное магнитное поле М (будем считать, что
Оно направлено по оси х и имеет градиент Так как в нематической фазе директор ориентируется вдоль поля (гл. 2 разд. 2), то намагниченность пропорциональна %|| (напомним, что ось Х выбрана вдоль направления директора). При наличии магнитного момента на образец будет действовать сила К в направлении градиента [199]:
K=-Jll (у. — /л) &В*1дх) dV = ± JT‘ (у — Xi) V (дВ*/дх)ач.
(3.11)
Здесь х — объемная восприимчивость образца, A Xi — объемная восприимчивость газа, вытесненного образцом. Если газ диамагнитный, величина мала, не зависит от температуры, и ею можно пренебречь. Используя восприимчивость на единицу массы, можно записать выражение (3.11) в виде
К = V&ldx)^ (3.12)
Силу К и массу т можно измерить с помощью чувствительных весов. Из найденных значений следует вычесть соответствующие величины для пустой ячейки. Величину (дВ2/дх)яу можно определить, выполнив аналогичные измерения для эталонной жидкости с известной восприимчивостью. Если величина DB2idx непостоянна в пространстве, которое занимает образец, то необходимо, чтобы эталонная жидкость занимала по возможности тот же объем и находилась в том же положении между полюсами магнита, что и исследуемое вещество. Тогда с приемлемой точностью
Xm=(OTref)("*refM)Xrmef • (3-13)
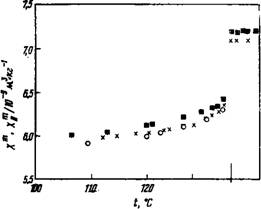
Часто измерения проводят в атмосфере гелия. Это не является строго необходимым, но в случае измерений на воздухе имеет относительно высокое значение и зависит от температуры, поскольку воздух (из-за присутствия в нем кислорода) парамагнитен. При этом необходимо вернуться к уравнению (3.11), чтобы вычислить поправку к уравнению (3.13). Несмотря на то что эта поправка невелика (несколько процентов), для немати — ческих жидких кристаллов она важна, так как в этом случае Xair зависит от температуры. Подробное описание подобных экспериментов приведено в работах [173, 92]. Хотя для нематической фазы можно измерить только % ц, однако можно найти х Для изотропной фазы и с помощью уравнения (3.5) получить полную информацию относительно А х — Приведенные на рис. 3.1 данные
|
150 N4 т Рис. 3.1. Магнитная восприимчивость ПАА. ■ данные работы [93]; X Данные работы [58]; О данные работы [53]. |
Показывают хорошее совпадение результатов для ПАА, полученных таким методом разными авторами. Что касается соединения МББА, то в этом случае наблюдается существенное расхождение результатов [93]. Для определения величины А^ использовался также метод вращающегося поля [58], но полученные этим методом результаты, как правило, оказывались слишком низкими.
Анизотропию магнитной восприимчивости можно использовать как параметр ориентационного порядка в нематической фазе. Эта анизотропия удовлетворяет требованиям, которые предъявляют к параметру порядка, так как она исчезает выше температуры TNi И принимает конечное значение ниже точки фазового перехода (точки просветления). Выбор именно магнитной восприимчивости обусловлен тем, что диамагнитные моменты молекул очень малы и их взаимодействием можно пренебречь. Такое заключение может быть сделано на том основании, что относительная диамагнитная проницаемость fAr = 1 X не~ значительно отличается от единицы. Следовательно, поле, действующее на молекулу, можно считать равным внешнему полю, и это облегчает интерпретацию результатов на молекулярном уровне. Параметр порядка Q определяется, как правило, формально, причем выделяется анизотропная часть х [61]
Здесь бар — символ Кроиекера, равный единице при а = Р и нулю в остальных случаях; Q представляет собой тензор втог — рОго ранга, имеющий диагональную форму, если ось z выбрана1 вдоль вектора п. Тензор имеет нулевой след и становится равным: нулю в изотропной фазе. Поэтому в случае цилиндрической симметрии относительно п достаточно рассмотреть только одну компоненту Q, например
C« = — J-(Z|—/i)- <315>
Действительно, вся необходимая информация содержится в величине
Чтобы дать интерпретацию результатам измерения восприимчивости на молекулярном уровне и связать параметр порядка Q с параметром микроскопического порядка S, введем тензор магнитной поляризуемости одной молекулы х. Этот тензор имеет диагональную форму в системе координат 5, т), С, связанной с молекулой, если ось С, направлена вдоль длинной оси молекулы. Если рассматривать молекулу как жесткий цилиндрически — симметричный стержень (первая модель, гл. 1), то диагональные
Компоненты тензора х будут = *г: и Xt = +
В этом случае интерпретация Q особенно проста: приложение магнитного поля в направлении директора индуцирует у молекулы магнитный момент ш. Обозначая угол между вектором п и осью С молекулы через 0, найдем компоненты т:
Mt = Ц^Х/ В^Cos 6, mt = i~lxt}B sin 6 . (3.16)
Для магнитного момента, направленного вдоль оси Z, в свою очередь получаем
Ш и = ц-1 (х^ Cos2 6+х, sin2 6) 5. (3.17)
Поэтому средний момент вдоль оси z равен
<**!> = Но-1 (*i <ccs2 0> + ** <sin2 0» В’ (3-18>
Или^ вводя параметр S, имеем
<*>» ="7 К(25 + 1) + х((2-25)]. (3.19а)
Аналогично
<х>,’=4-1*|(1—5) + М2+5)]- (З-196)
О
Эти выражения в действительности верны не только для магнитной поляризуемости, но и для макроскопических средних любого тензора, описывающего одноосную анизотропию на молекулярном уровне. Подобные выражения встречаются при описании различных макроскопических физических свойств. Если N — число молекул, то из уравнения (3.19) находим компоненты восприимчивости:
Хр =ЛГ <*>„ =± Xl(2S + i) + -/A(2-2S)],
(3.20)
= Л — (Х)х = ± /А (1 _ S) + /((2 + S)],
Где х I — и х T — — главные значения восприимчивости для случая идеального ориентационного порядка (S = 1). Разность этих выражений дает искомую разность Хи —Х± Или Qzz:
Z,-Xx = (X,-Zt)5- (3.21)
Соотношение (3.21) представляет собой выражение Цветкова для параметра порядка [181]. Отметим, что Х» —Х± и X i — — Х< соответствуют одним и тем же значениям температуры и плотности. Этот факт автоматически учитывается при использовании аналогичных выражений для молярных восприимчи — востей.
Если молекулы нельзя считать аксиально-симметричными, ситуация слегка усложняется. В рамках второй модели (гл. 1), согласно которой у молекулы имеются две взаимно перпендикулярные плоскости симметрии, для определения ориентации молекулы необходим кроме угла 0 еще и второй эйлеров угол гр. Тогда уравнение (3.17) заменяется на уравнение вида
Т (| = (Li"1 [ cos2 G + ( х.. sin2 + итт cos2 г|?) sin2 0] В =
Где Iz— z-компонента единичного вектора, направленного вдоль оси г] или ч соответственно. Отсюда находим
Х| = ЛГ 2 "«<*!>•> (3.23)
I
И магнитная анизотропия определяется выражением
Q:z = N 2 *И > <3-21)
. 6 б .
В котором используется обобщенный параметр порядка Sti
|
(3.25) |
|
Ii |
1
SH = (Y lz—* = С-
Поскольку след S равен нулю, существуют два независимых скалярных параметра порядка, в качестве которых (как и в гл. 1) выбираем S = S^ и D = SЩ — S^. Используя для компоненты Qгг выражение (3.15), получаем из уравнения (3.24) [2]
(X„ —Хл.)/^ «= [Х{.-L (ХК +xrtT)]s + -L (x^-x^ZM3.26)
Этот результат сводится к выражению (3.21), если х^ = х^, или если D = 0.
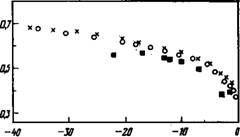
Чтобы найти параметр порядка Q 22, о существовании которого свидетельствует отличие нематической фазы от изотропной, достаточно измерить разность Хц —Х±- Однако из уравнения (3.26) следует, что средняя степень ориентации молекул определяется, по существу, двумя параметрами, которые не могут быть найдены с помощью одного эксперимента. Только если предположить, что D — 0, то анизотропия магнитной восприимчивости будет прямо пропорциональна микроскопическому параметру порядка S. Для выяснения, правильности подобного предположения необходимо дополнить результаты магнитных измерений данными исследований с применением других методов, например ядерного магнитного резонанса (ЯМР). По орто-про — тон-протонному взаимодействию в ПАА и следующем высшем гомологе — гс-азоксифенетоле (ПАФ) можно определить величину S как функцию температуры [175]. Это взаимодействие зависит от ориентации векто. ра, соединяющего протоны. Поскольку угол между этим вектором и длинной осью молекулы мал, результаты измерения S практически не зависят от D. Из рис. 3.2 видно, чт. о имеется хорошее согласие полученной таким образом величины S со значением, рассчитанным по магнитной восприимчивости с помощью уравнения (3.21) при разности % i — X t — ~ 0,69-10~9 м3/моль. Это означает, что в пределах точности эксперимента величину D можно считать очень малой.
Рассмотрим теперь результаты определения параметра порядка по химическому сдвигу тгара-углерода-13 [165], зависящему не Юлько от параметра S, но также и от величины D вследствие анизотропного характера экранирования бензола. Тем не менее; снова щшагая D = 0, получаем хорошее согласие со значениями найденными другими методами (рис. 3.2). Приведенные сравнительные данные зависят от относительной точности двух независимых. методов измерений, которая может быть и не очень высокой. ‘ Наиболее надежные абсолютные результаты
можно получать на основе данных ЯМР, поскольку этот метод позволяет с помощью одного эксперимента найти различные константы связи. Предварительно данные такого рода показывают, что величина D действительно очень мала или равна нулю [50, 81]. Поэтому при дальнейшем изложении материала будем считать D =0.
|
T-tM. x |
Б
|
|
|
|
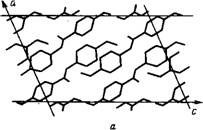
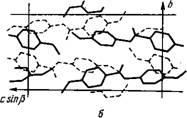
При расчете S для ПАА и ПАФ по анизотропии магнитной восприимчивости использовалось значение % t — % t = 0,69 х X 10"® м3/моль, которое было выбрано с целью получения хорошего согласия с данными ЯМР для обоих соединений. В принципе разность % I — х T может быть найдена по измерениям, выполненным на твердом монокристалле. Единственное немато — генное соединение, для которого были проведены такие измерения, — это ПАА [53], кристаллизующийся в моноклинной системе [111, 21]. В качестве оси £ следует выбрать ось, проходящую через внешние атомы углерода азоксибензольной части молекулы. Для различных молекул эта ось составляет с плоскостью симметрии единичной ячейки угол ±6,1°, а ее проекции на эту плоскость параллельны друг другу (рис. 3.3). Направление, в котором восприимчивость максимальна, лежит в плоскости симметрии и составляет с осью С угол 8,8°. Если приближенно считать кристалл ПАА одноосным, то получаем значение % i — % t = 0,77-10"9 м3/моль. Поскольку эта величина представляет собой разность двух значительно больших величин, точность ее определения, по-видимому, не превышает 10%. Приведенное значение разности х I — X T сравнивается с аналогичными данными для бифенила и некоторых других веществ с двумя бензольными кольцами, принадлежащих к классам хорошо известных нематических соединений (табл. 3.1). В большинстве случаев значение х I — X T несколько ниже удвоенного значения для бензола, причем единственным исключением является ПАА.
Таблица 3.1
Молекулярный диамагнетизм некоторых соединений (10 • м9/моль) [156]
-0,438 -0,438 -1,189 0,374
-0,851 -0,775 -2,310 0,690
-1,216 -1,107 -3,409 1,042
-1,024 -0,852 -2,492 0,648
-1,375 -0,946 -2,597 0.397
-1,141 -1,141 -2,542 0.701
-1,078 -0,630 -2,634 0,553^
-0,985 -0,679 -2,430 0,569^
|
|
-1,130 -3,079 0,774
|
Рис. 3.3. Кристаллическая структура ПАА. А—Проекция на плоскость, перпендикулярную оси второго порядка; б—Вид вдоль ОСИ С [2;1]. |
Значение % T — х T Для ПАА и ПАФ, использованное при расчёте данных рис. 3.2, хотя и несколько ниже, чем для твердого ПАА, тем не менее согласуется с общей тенденцией.
|
|
Наконец, отметим, что для оценки разности х I — X T может быть также использован метод экстраполяции: логарифмическая зависимость хн — Х± от температуры часто оказывается линейной, и величину х I — X T получают экстраполяцией данных к Г = 0. При этом предполагается, что S = 1 [73], а формула вида (1.6), не имеющая теоретического обоснования, тем не менее справедлива вплоть до Т = 0. Установлено, что для ряда
|
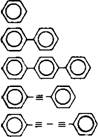
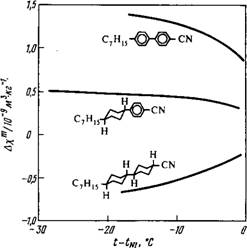
Рис. 3.4. Магнитная восприимчивость некоторых соединений с различным числом бензольных колец. |
Из ПАА и высших гомологов получаемое таким образом значение X I — % t несколько изменяется с увеличением длины цепи. Поскольку вклад парафиновых цепей в анизотропию восприимчивости довольно мал, это означает, что метод экстраполяции не обеспечивает высокой точности результатов.
Диамагнетизм обусловлен возникающей под действием магнитного поля лармовской прецессией электронов, вращающихся вокруг ядер. Это приводит к появлению наведенного магнитного момента, направленного противоположно внешнему полю, и поэтому величина х отрицательна. Поскольку атомная восприимчивость изотропна, можно ожидать, что анизотропия магнитной восприимчивости молекул также мала. Однако у ароматических систем наблюдается сильная анизотропия 170]. Качественно это можно объяснить тем, что л-электроны бензольного кольца де — локализованы и образуют «кольцевой ток». Следовательно, когда магнитное поле перпендикулярно плоскости кольца, можно ожидать появления большого наведенного момента, направленного против создающего его поля (сравните х^ в табл. 3.1). В соответствии с уравнением (3.21) можно предположить, что в случае нематических жидких кристаллов анизотропия восприимчивости должна быть положительной и пропорциональной числу ароматических колец. Такая зависимость действительно наблюдалась авторами работы [193] и иллюстрируется на рис. 3.4. Для соединений с двумя бензольными кольцами величина Дхт имеет порядок 10~9 м3/кг. При каждом замещении бензольного кольца циклогексановым анизотропия восприимчивости падает. Если ароматические кольца в системе отсутствуют, величина Ахт становится отрицательной, что является следствием отрицательной анизотропии связей C=N [52]. Из табл. 3.1 видно, что аналогичный эффект наблюдается и для других тройных связей. Особенно заметно понижает значение х I — X T мостик —С=С— —С=С— . Качественно этот эффект может быть связан с кольцевыми токами, которые" в случае тройных связей могут возникать в плоскости, перпендикулярной длинной оси молекулы. Следовательно, сочетание этого мостика с циклогексановыми кольцами и CN-группами может дать нематический жидкий кристалл с относительно большой отрицательной анизотропией диамагнитной восприимчивости.
 18 января, 2013
18 января, 2013  admin
admin 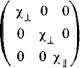
 Опубликовано в рубрике
Опубликовано в рубрике 