Е. В. Голикова, Ю. М. Чернобережский
(Ленинградский технологический институт целлюлозно-бумажной промышленности)
Один из наиболее сложных и мало разработанных вопросов коллоидной химии — взаимосвязь между интенсивностью взаимодействия дисперсных частиц со средой и их агрегативной устойчивостью.
Физическая теория устойчивости лиофобных коллоидов (теория ДЛФО) является в настоящее время фундаментом всех исследований в области устойчивости дисперсных систем. Она
Нашла блестящее подтверждение в большом количестве экспериментальных работ и продолжает интенсивно развиваться. Так, в частности, предприняты попытки распространить ее применение на системы, характеризующиеся значительным взаимодействием частиц с дисперсионной средой. С этой целью Б. В. Дерягиным и Н. В. Чураевым введено представление о структурной составляющей расклинивающего давления, связанной с перекрытием граничных слоев (ГС) жидкости, окружающей взаимодействующие частицы [47, 422, 463—465]. На основании многих экспериментальных данных в настоящее время можно считать, что структура слоев жидкости вблизи поверхности раздела отлична от структуры объемной жидкости [87, 114, 446—472]. В случае лиофильных поверхностей такие структурные изменения распространяются на значительные расстояния от твердой поверхности (до десятков нанометров).
Большое число работ убедительно демонстрирует отличие свойств жидкости, находящейся вблизи поверхности, от свойств в ее объеме [14, 36, 87, 114, 466—475]. Так, обнаружена аномалия диэлектрических свойств [469, 470], эффект скачкообразного изменения электропроводности [470], изменение вязкости в зависимости от расстояния до твердой стенки [114, 471, 472], появление предельного напряжения сдвига жидкости при приближении к поверхности твердого тела [14, 473, 474]. Для набухающего в водных растворах Ыа-замещенного монтмориллонита обнаружена оптическая анизотропия тонких прослоек воды [36]; найдено изменение теплоемкости смачивающих пленок нитробензола на силикатных поверхностях [475]. Установлено отличие ГС от объемной жидкости по растворяющей способности, температуре замерзания, теплопроводности, энтальпии. В. Дрост-Хансеном опубликованы обзоры большого числа работ, содержащие как прямые, так и косвенные свидетельства структурных изменений в граничных слоях [476—478]. В качестве косвенных доказательств автор приводит, в первую очередь, существование изломов на кривых температурной зависимости ряда свойств поверхностных слоев. Эти температуры отвечают, согласно Дрост-Хансену, разной перестройке структуры ГС. Широко известны также работы Г. Пешеля [479] по исследованию ГС жидкостей (и, прежде всего, воды) у поверхности кварца в присутствии ряда электролитов.
Структурные изменения воды в ГС подтверждаются спектральными методами [479—484], а также согласуются с результатами расчетов структуры тонких прослоек методами молекулярной динамики и Монте-Карло. Изменение структуры воды на больших расстояниях от поверхности частиц прямо подтверждено методом ядерного магнитного резонанса [66, 71, 73, 315]. Таким образом, во многих экспериментальных исследованиях обнаружено существенное отклонение структурно-чувствительных свойств ГС жидкостей на лиофильных или лиофилизи- рованных поверхностях.
Для ряда случаев, когда наблюдается скачкообразное изменение ряда свойств при переходе от пристенных слоев к объемной фазе (что соответствует фазовому переходу первого рода) и когда структурно-модифицированные слои ГС отделены резкой границей от жидкости в объеме, Б. В. Дерягиным была выдвинута концепция «особых граничных фаз».
Ориентация молекул в ГС жидкостей, повышение вязкости, упругости, появление сопротивления сдвигу могут значительно препятствовать сближению частиц. Перекрытие ГС при сближении частиц приводит к появлению структурной составляющей расклинивающего давления, ответственной за устойчивость ряда гидрофильных коллоидов и а-пленок воды на гидрофильных подложках. В случае гидрофобных поверхностей структурные силы могут приводить к дополнительному притяжению частиц («гидрофобное взаимодействие»).
Протяженность ГС и степень их структурирования в общем случае должны зависеть от свойств подложки, природы растворителя, температуры и концентрации растворенных веществ. Известные к настоящему времени факты указывают на значительное структурирование жидкости в ГС, но не дают ответа на вопрос о характере изменения структуры по мере удаления от подложки. По-видимому, одним из наиболее чувствительных к изменению структуры свойств является вязкость, однако применяемые методы ее определения [114, 424, 425, 438] не дают однозначной информации о строении ГС. В общем случае она может изменяться при удалении от поверхности раздела фаз как ступенчато, так и непрерывно. В работе [114] показано, что существенные отличия в характере изменения вязкости могут проявиться при перекрывании ГС.
Представления о наличии в структуре ГС периферийной части с разрушенной молекулярной структурой — «подплавленно — го слоя» — высказаны в работах [100, 126, 485]. Трехслойная модель ГС, предложенная в [485], была развита далее в работах [476]. В. Дрост-Хансен предполагает существование различных типов структурированной воды [477]. На близких расстояниях (5—10 молекулярных диаметров) структурирование может возникать за счет ион-дипольного и диполь-дипольного взаимодействия («высокоэнергетическое»). Структурирование на больших расстояниях (до сотен молекулярных диаметров) может протекать за счет кооперативных «низкоэнергетических» взаимодействий. Такой подход позволяет объяснить немонотонную зависимость расклинивающего давления от температуры, найденную Г. Пешелем и сотр. [479, 487]. Наличие максимумов расклинивающего давления в этом случае обусловлено резкими структурными перестройками ГС, происходящими в исследованном интервале температур (0—60°С). В узком температурном интервале на первом этапе структурных изменений в ГС возникает некоторый молекулярный беспорядок, который, в свою очередь, облегчает образование новой структуры с пониженной энтропией. Несмотря на возможность образования некоторых новых структур, рост интенсивности теплового движения молекул при дальнейшем повышении температуры ведет к разрушению водородных связей, что приводит к уменьшению зоны структурных изменений и к росту энтропии [486].
В работах [30, 488] изучено влияние температуры на толщину полимолекулярных адсорбционных пленок воды на поверхности плавленого кварца. Если при ^>65 °С толщина пленки не превышает монослоя, то при 10 °С она составляет приблизительно 10 нм. Температурная зависимость ряда свойств, таких, как теплопроводность [489, 490], вязкость [491], амплитуда колебаний частиц при электрофорезе в переменном поле вблизи подложки [492], скачкообразно изменяются при 65—70 °С. Такое поведение, так же как и исчезновение эффекта термоосмоса вблизи 70 °С [463], авторы объясняют полным разрушением ГС.
На состояние молекул воды в ГС влияют также природа подложки и состав раствора. В. Дрост-Хансеном [493], Я. Из — раелашвили [494, 495] рассмотрено состояние ГС вблизи полярной и неполярной поверхности. Нерастворимые примеси поверхности, как и ее выщелачивание, в определенной степени влияют на ГС, однако, как отмечают Б. В. Дерягин и Н. В. Чураев [422], эффект выщелачивания не играет значительной роли. Предварительная обработка поверхности, примеси [422, 480, 494,
496] , а также время контакта поверхности со средой [479, 490,
497] могут в значительной мере влиять на состояние ГС, что также свидетельствует о большой роли активных групп поверхности в образовании ГС.
Введение различных примесей в раствор способствует изменению толщины ГС, а в некоторых случаях и их образованию [428]. А. И. Русанов и соавт. [498] проследили зависимость протяженности ГС на кварце от состава смеси полярной и неполярной жидкости и нашли, что максимальной толщине отвечает мольная доля полярного компонента, приближающаяся к единице. Введение электролита в воду также может влиять на структуру ГС. Это направление исследований представляет значительный интерес, поскольку затрагивает фундаментальный вопрос о влиянии гидратации ионов на структурирование воды. Так, сильное влияние иона NO3- на коагуляцию положительно заряженных латексов полистирола было объяснено его слабой гидратацией [499]. Г. Пешель и П. Белоушек [479] приводят ряд 1~>Вг->С1-, в котором усиливается разрушающее влияние аниона. Согласно этим же авторам [479, 500], обнаруженная экстремальная зависимость структурной составляющей расклинивающего давления от концентрации электролита на кварце может быть результатом перехода между двумя типами соль — ватных структур, отвечающих разбавленным и концентрированным растворам электролитов.
Согласно ГІешли, «гидратные» (точнее, структурные) силы могут возникать как на гидрофильных поверхностях с гидрати — рованными полярными или ионными группами, так и на поверхностях, которые вначале не являются гидрофильными, но могут изменяться при адсорбции гидратированных форм и вести себя как гидрофильные («вторичная гидратация») [121]. В основе теории «гидратных» сил лежит положение о поверхностной адсорбции гидратированных ионов. Анализ явления показывает, что действие «гидратных» сил определяется не только плотностью адсорбированных катионов, но и изменением свободной энергии, связанным с замещением катионом иона Н3О4". Силы гидратации проявляются в достаточно концентрированных растворах (более Ю-4 моль/л), и их величина определяется положением ионов в лиотропном ряду. Этот механизм, согласно которому взаимодействие гидратированных катионов приводит к возникновению сил отталкивания между поверхностями с достаточно высокой плотностью поверхностного заряда и слабой способностью к образованию водородных связей, может объяснить высокие пороговые концентрации, необходимые для коагуляции амфотерных частиц латекса полистирола [501] и золя Si02 [502].
Следует подчеркнуть, что эффект разрушающе-структури- рующего влияния ионов на ГС должен зависеть от концентрации ионов; вторичная гидратация наиболее ярко проявляется при достаточно высоких константах комплексообразования и вдали от изоэлектрической точки, а также на поверхностях, активные группы которых не способны (или обладают слабой способностью) образовывать водородные связи с молекулами воды. Приведенные выше возможные механизмы влияния ионов на ГС необходимо учитывать при рассмотрении устойчивости конкретных дисперсных систем.
Наличие на поверхности частиц групп, способных образовывать водородные связи, определяет возможность эпитаксиально — го механизма образования ГС. Так, исключительно высокая устойчивость золя Si02 вблизи изоэлектрической точки [24, 502, 503] может быть также объяснена наличием граничных слоев значительной толщины, образованных при ориентации молекул воды за счет водородных связей около незаряженной поверхности, несущей недиссоциированные силанольные группы.
Значительное влияние ГС на устойчивость коллоидов обсуждалось в ряде работ. Так, обнаруженную «аномальную», не объясняющуюся классической теорией ДЛФО, устойчивость золя арахиновой кислоты [504] и октадеканола [505] авторы связывали с наличием у поверхности частиц структурированной воды, обусловливающей наличие добавочных сил отталкивания. К аналогичному заключению пришли авторы работы [506], в которой изучалась кинетика коагуляции монодисперсных ла — тексов поливинилацетата, а также времена ЯМР-релаксации воды в системе в зависимости от температуры и концентрации частиц. Отсутствие корреляции между электрофоретической подвижностью частиц и устойчивостью, характерной для лио — фобных коллоидов, наблюдалось для золей кремнезема [502, 503, 507]. В таких системах пороги коагуляции достигают значительных величин, причем устойчивость золей падает с увеличением заряда поверхности. Л. Аллен и Е. Матиевич [502] объясняют наблюдаемую зависимость устойчивости золей Si02 от концентрации электролита обменом протонов силанольных групп поверхности Si02 на катионы электролита. Устойчивость системы при низких рН, когда ионный обмен невелик, авторы связывают со значительной гидратацией поверхности.
При изучении закономерностей седиментации суспензий аэросила в бензоле и нитробензоле было показано, что объем осадка в бензольной суспензии больше, чем в нитробензольной [496]. Найденное различие объяснено стабилизирующим влиянием граничной фазы нитробензола на суспензию аэросила. Повышение температуры приводило к уменьшению агрегатив — ной устойчивости суспензии аэросила в нитробензоле и росту седиментационного объема осадка, что было объяснено уменьшением равновесной толщины граничной фазы нитробензола. Обработка аэросила фтороводородной кислотой дезактивировала поверхность и способствовала появлению чрезвычайно рыхлых коагуляционных структур, тогда как при обработке хромовой кислотой происходила активация поверхности частиц, что облегчало образование на них граничной фазы нитробензола и приводило к получению устойчивой суспензии, дающей плотный осадок.
Все приведенные выше экспериментальные факты и даваемые им объяснения свидетельствуют о той исключительно важной роли, какую играет интенсивность взаимодействия частиц со средой в явлении устойчивости коллоидов. Остановимся более подробно на ряде данных, полученных авторами настоящей работы, подтверждающих важную роль ГС в устойчивости дисперсных систем. Объектами исследования являлись дисперсия Si02, полученная помолом горного хрусталя с последующим выделением фракции («0,2—0,3 мкм), и дисперсия природного алмаза (размер частиц »0,5 мкм).
Исходный золь кварца в воде был агрегативно устойчивым, изоэлектрическая точка частиц Si02, оцененная методом микроэлектрофореза, находилась при рН = 2 [24]. Методом поточной ультрамикроскопии было показано, что золь Si02 в области изоэлектрического состояния и при щелочных рН (рН 9— 11) является агрегативно устойчивым при концентрациях добавленного электролита К. С1 10-3-г-10-1 моль/л, тогда как в промежуточной области рН (от 3 до 6) золь может быть легко коагулирован раствором КС1. Таким образом, устойчивость золя Si02 является экстремальной функцией рН с минимумом, лежащим в интервале рН = 3-^6. Последовательное изменение рН золя Si02 (концентрация К. С1 1-Ю-1 моль/л, рН = 9) в ряду рН 9 рН 6 рН 3 рН 2 при введении хлороводородной кислоты приводило сначала к потере устойчивости (при рН = 6 и еще в большей степени при рН = 3), а затем к рестабилизации золя (при рН = 2). Эти данные также можно рассматривать как дополнительное доказательство экстремального характера зависимости устойчивости от рН. Например, высокозаряженный золь кварца при рН = 6 ведет себя как типичный ионостабили — зированный коллоид, чувствительный к добавлению небольших количеств электролита. В то же время при рН = 2 (область изоэлектрического состояния), а также при рН, равных 9 и 11, он становится практически ионоиндифферентным. Эти факты можно объяснить появлением в указанных областях рН сил отталкивания неэлектрической природы.
Изменение устойчивости при изменении кислотности среды и незначительном изменении ионной силы может быть объяснено влиянием рН на свойства поверхности Si02 и, вследствие этого, на свойства и протяженность ГС. При щелочных рН образование ГС может быть связано с ориентацией диполей воды под действием сильного электрического поля поверхности частиц Si02 (ж 10s В/см). Следует отметить, что при рН = 9-^-11 существенную роль в устойчивости частиц кварца могут также играть поверхностные гелеобразные слои поликремниевых кислот. При рН = 2 наблюдаемая устойчивость системы может быть обусловлена ориентацией молекул воды за счет водородных связей, возникающих около незаряженной поверхности, несущей недиссоциированные силанольные группы [502, 503, 508]. Таким образом, для золя Si02 в случае как незаряженной, так и высокозаряженной поверхности частиц возможно образование достаточно «толстых» и «прочных» ГС, что обусловливает высокую агрегативную устойчивость системы. В промежуточной области (рН = 3-=-6), где с одной стороны, часть силанольных групп уже диссоциирована, а с другой стороны, плотность фиксированного заряда еще недостаточно велика, развитие ГС является минимальным.
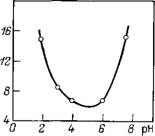
На основе одновременного рассмотрения экспериментальных данных зависимости степени агрегации частиц от концентрации добавленного электролита с результатами расчетов по теории ДЛФО нами была предпринята попытка оценки толщины ГС у поверхности Si02. Было показано, что в зависимости от рН
Рис. 10.1. Зависимость толщины граничного слоя на частицах кварца от рН
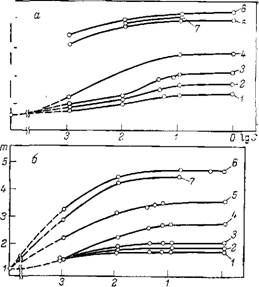
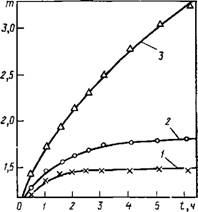
Протяженность ГС изменяется в пределах 6—16 нм (рис. 10.1), что согласуется с толщиной а-пленок воды на кварце [45]. Для дальнейшего изучения роли структурной составляющей в устойчивости золя SiOa было проведено ультрамикроскопическое изучение коагуляции частиц кварца в присутствии хлоридов Li, Na, К, Cs, Mg, Са, Sr и Ва в широком интервале их концентраций 1-Ю"3—1 моль/л. На рис. 10.2 представлены зависимости степени агрегации частиц т от концентрации добавленного электролита. Степень агрегации т = По/п отвечает установлению динамического равновесия между процессами агрегации и распада частиц. Прослеживается четкая зависимость влияния ионов лиотропного ряда на степень агрегации частиц. При относительно невысоких концентрациях 1 : 1-электролита (^10~2 моль/л) рост степени агрегации в лиотропном ряду связан с ростом адсорбционной способности ионов и, соответственно, с уменьшением потенциала Штерна, что должно приводить к понижению ионно-электростатической составляющей энергии взаимодействия частиц и углублению вторичной ямы. При более высоких концентрациях 1 : 1-электролита (>10-2 моль/л) энергетический барьер, как показывают расчеты, исчезает, и обратимый характер агрегации обусловлен уже ограниченной глубиной первичной ямы. Появление сил отталкивания на малых расстояниях, как и ограниченность глубины первичной ямы, определяются взаимодействием ГС частиц Si02. В этой же области концентраций наблюдалась зависимость степени агрегации от положения катиона в лиотропном ряду. Это позволяет высказать предположение, что вклад структурной составляющей в ряду LiCl>NaCl>KCl>CsCf уменьшается. Это может быть обусловлено уменьшением протяженности ГС в данном ряду электролитов. Аналогичные рассуждения могут быть приведены и для объяснения коагуляции дисперсии Si02 в растворах MgCl2, СаС12, SrCl2 и ВаС12.
|
H, нм |
Определенный интерес для понимания роли ГС в устойчивости коллоидов представляет модифицирование поверхности частиц в процессе адсорбции ПАВ, которое должно оказывать влияние на свойства и протяженность ГС. Структурные силы, проявляющиеся при сближении частиц, будут зависеть в этом случае от величины адсорбции ПАВ, степени завершенности первого и второго адсорбционных слоев, определяющей гидро — фобизацию или гидрофилизацию поверхности частиц. С этой
целью нами была исследована устойчивость золя кварца в присутствии катионоактивного ПАВ — цетилтриметиламмонийбро — мида (ЦТАБ). Исследование коагуляции проводилось, как и ранее, методом поточной ультрамикроскопии. Для различных концентраций ЦТАБ (Ю-6—10~3 моль/л) и рН, равных 3 и 6,. а также при добавлении КВг были получены зависимости обратной концентрации частиц от времени, прошедшего с момента введения ЦТАБ. Кривые l/n{t) имеют в большинстве случаев S-образную форму, причем агрегативное равновесие в системе наступает через 20—25 ч после начала эксперимента и сохраняется в течение продолжительного периода времени. На рис. 10.$ приведена зависимость степени агрегации частиц золя Si02 or логарифма концентрации ЦТАБ.
|
Рис. 10.2. Зависимость степени агрегации золя SiCb при рН=3 (а) и рН=6 (б) от концентрации электролита: / — LiCl; 2 —NaCl; З — КС1; 4- CsCl; 5 —MgCl2; 6 — ВаСЬ; 7 — SrClj |
|
OigC |
Для анализа полученных данных в свете теории ДЛФО нами были проведены расчеты энергии взаимодействия частиц. Si02 в приближении взаимодействия двух сфер, а также двух плоских поверхностей [509]. Поскольку концентрация ЦТАВ была сравнительно небольшой, в расчетах допускалось, чтс* различием между потенциалом г^ и ^-потенциалом можно пренебречь. Агрегативно устойчивый в воде золь Si02 при введении в систему ЦТАБ (концентрация 1-Ю-6 моль/л) начинает агрегировать. При концентрации ЦТАБ 1-Ю-5 моль/л ^-потенциал частиц Si02 резко изменяется (до —5,3 мВ по сравнению с —62 мВ в воде), а степень агрегации частиц возрастает до 2,2. Из расчета энергии взаимодействия следует, что при данной т — Концентрации ЦТАБ 5- высота энергетического барьера составляет 4. около 6 kT, а вторичный минимум крайне 3. мал (доли kT). Кроме того, его положению 2 отвечает расстояние «800 нм, что также де- 1 Лает практически не
Рис. 10.3. Зависимость степени агрегации m (/) и ^-потенциала (2) частиц кварца от концентрации ЦТАБ при рН 6.
Пояснения см. в тексте
Рис. 10.4. Зависимость степени агрегации частиц SiCb от концентрации
ЦТАБ:
/ — при рН=3; 2 — при рН=6 в присутствии 1 ■ 10—1 М КВг
Возможной взаимную фиксацию частиц на дальних расстояниях. Таким образом, на участке а (см. рис. 10.3) коагуляция может происходить лишь в первичном минимуме. Как показали микро — электрофоретические измерения, с ростом концентрации ЦТАБ ^-потенциал частиц Si02 уменьшается и при концентрации 2,5-Ю-5 М происходит практически полная «нейтрализация» частиц (£ = 0) вследствие адсорбции положительно заряженных ионов ЦТА+ (см. рис. 10.3). Однако по мере приближения к изоэлектрической точке, в которой степень агрегации частиц составляет всего 1,2, устойчивость системы возрастает.
Принимая, что посадочная площадка иона ЦТА+ составляет 0,2 нм2 [510] и учитывая развитые в работе [511] представления, можно найти степень покрытия поверхности частиц кварца ионами ПАВ вблизи изоэлектрической точки. Как показал расчет, оиа составляет около »0,1%. Учитывая этот факт, низкую степень агрегации и ее обратимый характер можно объяснить на основе концепции ГС. При нейтрализации поверхностного заряда ионами ЦТАБ вблизи изоэлектрической точки образуются, вероятно, более «прочные» и протяженные ГС, что может быть связано с возникновением более благоприятных условий для развития водородных связей на силанольных группах теперь уже незаряженной поверхности БЮг — Это некоторым образом аналогично случаю увеличения протяженности ГС при снижении степени диссоциации силанольных групп на поверхности кварца при приближении к изоэлектрической точке [24].
Увеличение концентрации ЦТАБ в системе после достижения; изоэлектрического состояния (>2,5-10~5 М) приводит к росту положительных значений электрокинетического потенциала. Однако степень агрегации частиц (вплоть до концентрации ЦТАБ Ю-4 М) вновь начинает расти, что может быть обусловлено разрушением ГС при появлении заряда на поверхности частиц, а также некоторой гидрофобизацией поверхности при адсорбции ПАВ. Гидрофилизация поверхности частиц Si02 за счет двуслойной адсорбции ЦТАБ [512] маловероятна вследствие низкой степени покрытия Si02 ионами ЦТАБ вблизи изоэлектрической точки. Из расчета энергии взаимодействия сферических частиц при С=Ы0~4 М следует, что коагуляция частиц во вторичном минимуме (доли kT) невозможна. Она происходит в первичном минимуме при преодолении энергетического барьера. Положительная структурная составляющая расклинивающего давления, ограничивающая его глубину, может быть обусловлена как взаимодействием ГС воды на поверхности Si02, так и взаимодействием адсорбционных слоев ПАВ. Можно ожидать, что при данной концентрации степень покрытия поверхности кварца молекулами ПАВ близка к 20% [513]. Как видно из рис. 10.3, дальнейшее увеличение концентрации ЦТАБ вновь приводит к ее стабилизации (участок г), что может быть связано — с образованием геми-мицелл на поверхности кварца, а также увеличением положительного значения £-по — тенциала частиц Si02.
На рис. 10.4 (кривая 1) приведены данные, характеризующие агрегацию золя кварца в присутствии ЦТАБ при рН = 3, когда исходный золь кварца уже агрегировал (степень агрегации т = 2,2). Видно, что при рН = 3, как и при рН = 6 наблюдается скачкообразное изменение устойчивости золя, однако полной стабилизации системы не происходит. Расчет энергии взаимодействия частиц Si02 по теории ДЛФО показывает, что наблюдаемая агрегация связана с первичным минимумом на кривой энергии взаимодействия частиц. Наличие структурной составляющей энергии взаимодействия, возникающей при перекрытии ГС воды, а также, возможно, адсорбционных слоев ЦТАБ на кварце, препятствует непосредственному сближению частиц и достижению высоких степеней агрегации.
Данные по агрегации частиц Si02 при рН = 6 под действием ЦТАБ в присутствии 0,1 М КВг показаны на рис. 10.4 (кривая 2). Наблюдаемый характер изменения степени агрегации частиц кварца от концентрации ЦТАБ в условиях сильно сжатого ДЭС также свидетельствует о значительной роли структурной составляющей расклинивающего давления в устойчивости данной системы.
Для получения представлений о свойствах и протяженности ГС у поверхности частиц кварца нами были исследованы зави-
|
|
Рис. 10.5. Схема строения двойного электрического слоя и смещения границы скольжения с ростом напряженности приложенного электрического ПОЛЯ
Симости электрофоретической подвижности частиц от напряженности электрического поля Н (2—20 В/см) в широком интервале рН (3—12). Измерения проводили на частицах кристаллического кварца с эквивалентным радиусом »0,23 мкм при постоянной ионной силе раствора’, равной 1 • Ю-2. При постановке этой части работы мы исходили из следующих общих представлений. На рис. 10.5 приведена обычная схема падения потенциала в ДЭС. Если принять, что вода в ГС является частично структурированной (обладает напряжением сдвига) и прочность структуры убывает по мере удаления от поверхности частицы, то рост напряженности внешнего электрического поля, приводящий к росту электрофоретической скорости частицы, будет вызывать, согласно Стоксу, рост силы трения, испытываемой частицей при движении. Результатом этого в свою очередь может стать разрушение наружной части ГС и смещение границы скольжения по направлению к частице на величину Дл;, так что большее значение ^-потенциала будет соответствовать большей напряженности внешнего электрического поля. Силу трения FrР и предельное напряжение сдвига Є можно рассчитать в первом приближении
По следующим формулам:
|
(10.1) (10.2) |
|
Чг |
РТр = 6яг)гК; Ftp 6лтУ V ЗГ)У
4л/"2
Где г — эквивалентный радиус частицы; V — электрофоретическая скорость частицы; т) — вязкость.
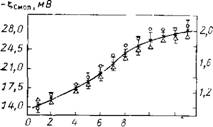
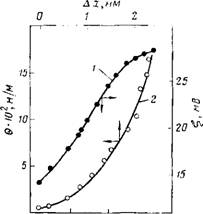
На рис. 10.6 приведена зависимость электрофоретической подвижности U и ^-потенциала частиц Si02 в растворе КС1 при рН = 3 от напряженности электрического поля Я, полученная на основании статистической обработки результатов измерений для 30 разных частиц при каждом заданном значении Н. Из рисунка видно, что с увеличением градиента потенциала от 100 до 1300 В/м величина U монотонно возрастает от 1-Ю-8 до 2-Ю-8 м2-с/В, а ^-потенциал изменяется соответственно от —14 до —28 мВ. Значения ^-потенциала рассчитывали по формуле Смолуховского без поправок на поляризацию ДЭС частиц SiC>2.
Наиболее вероятным объяснением наблюдаемой зависимости, как обсуждалось выше, является смещение плоскости скольжения жидкости по направлению к поверхности частицы по мере увеличения сдвиговых напряжений с ростом скорости движения частиц V. С ростом градиента потенциала приложенного поля все большая часть ДЭС вовлекается в движение и со ■смещением плоскости скольжения на расстояние Ах ^-потенциал приобретает" новое, более высокое значение = +
На основании формулы (10.2) были рассчитаны напряжения сдвига 9 для различных значений Н. Наблюдаемое изменение ^-потенциала в процессе увеличения напряженности электрического поля позволяет оценить величину смещения границы скольжения по следующей формуле:
£і=£2ехр (— kAx), (10.3)
Где k= [zFVSnCj(e,kT)]1/2 — обратный дебаевский радиус.
|
Ч-‘О’^1 ‘ В/м |
|
W Н-Ю, В/м |
|
Рис. 10.6. Зависимость электрофоре- ТИЧЄСКОЙ ПОДВИЖНОСТИ U И £смол частиц Si02 от напряженности электрического поля Н при рН=3 |
На основании проведенных расчетов получена зависимость в от АЛ: (рис. 10.7). Из этих данных следует, что возрастание Н приводит к росту величины смещения границы скольжения жидкости АЛ: по направлению к поверхности частицы и возрастанию сдвигового напряжения. Полученные данные свидетельствуют о неоднородности ГС, прочность которого возрастает по мере приближения к поверхности частицы. Обращают на себя. внимание небольшие величины (сотые доли Н/м2) предельного напряжения сдвига, относящиеся к периферийной области ГС. Эта величина резко возрастает (до десятых долей Н/м2) по
|
4 8 12 Н-102,В/м |
Рис. 10.7. Зависимость ^-потенциала и напряжения сдвига 0 от напряженности поля Н и смещения границы скольжения Ах
Мере приближения к поверхности (на 1—2 нм). Аналогичные зависимости £(#) и 9 (Ах) были получены и при других значениях рН. Таким образом, нахождение зависимости U(H) позволяет в общем случае получить определенные представления
0 напряжении сдвига и протяженности ГС у поверхности исследуемых частиц. Так, для частиц кристаллического кварца на основании полученных нами данных можно говорить о толщине ГС, превышающей 3 нм.
Результаты исследования электроповерхностных свойств и устойчивости дисперсии аморфного кремнезема [514] и расчеты энергии взаимодействия частиц по теории ДЛФО показали, что эта дисперсия более устойчива по сравнению с дисперсией кварца той же дисперсности. Наблюдаемые различия в устойчивости обеих систем при одном и том же составе дисперсионной среды (в том числе и при рН, соответствующих изоэлектри — ческому состоянию) объяснены разным вкладом структурной составляющей, т. е. структурными отличиями ГС у поверхности исследуемых частиц.
Другим объектом исследования была водная дисперсия природного алмаза (ПА) со средним размером частиц 0,5 мкм [515]. Результаты потенциометрического титрования порошка алмаза в фоновых растворах LiCl, КС1, CsCl, KNO3 и ВаС12 в широком интервале рН (3,5—10,5) и ионных сил (10_3, 10~2Г Ю-1) приведены в работе [516]. Из полученных зависимостей электрофоретической подвижности и ^-потенциала частиц ПА от рН в растворах электролитов 1:1 и 2: 1 (при ионных силах 10_3, 10~2 и 5-Ю-2) следует, что во всем исследованном интервале рН частицы ПА заряжены отрицательно и изоэлектриче — ская точка лежит в сильнокислой области (рН = 2). В случае
1 : 1-электролитов с ростом рН наблюдается возрастание отрицательного значения ^-потенциала, что обусловлено ростом степени диссоциации активных кислотных групп поверхности. При этом в случае ионных сил 10_3 и Ю-2 значения ^-потенциала в растворах LiCl и КС1 практически совпадают, а в растворах CsCl лежат значительно ниже. Наблюдаемые различия можна в определенной мере связать с изменением констант поверхностного комплексообразования (Кмеш), значения которых убывают в ряду CsCl>KCl>LiCl (p*/CMeint равны 0; 0,7 и 0,9 соответственно) [516]. При ионной силе 5-Ю-2 различие в электрофоретической поведении дисперсии алмаза в растворах хлоридов щелочных металлов становится незначительным.
В растворах ВаС12 во всем исследованном интервале рН (2—11) при ионных силах!0_3 и Ю-2 ^-потенциал имеет отрицательные значения, лежащие гораздо ниже, чем для растворов 1 : 1-электролитов. Значения ^-потенциала остаются практически неизменными во всем исследованном интервале рН, за исключением значений при рН = 3 и рН = 2, где ионную силу устанавливали, используя растворы НС1 и ионы Ва2+ отсутствовали. Можно предположить, что найденный характер зависимости £(рН) в растворах ВаС12 объясняется значительной специфической адсорбцией ионов Ва2+ на поверхности алмаза. Это подтверждает и найденное на основании данных потенциометриче — •ского титрования значение константы поверхностного комплек — сообразования (р/Сіп1ва2+=—0,6). По-видимому, с ростом рН при увеличении степени диссоциации поверхностных групп происходит эквивалентная адсорбция ионов Ва2+ на диссоциированных центрах поверхности.
Исследование устойчивости дисперсии ПА в растворах различных электролитов проводили методом поточной ультрамикроскопии. При рН = 2 и рН = 3 в широком интервале концентраций КС1 (от 1-Ю-2 до 3-Ю"1 М) дисперсия ПА является агре — гативно устойчивой. При концентрации 5-Ю-1 М при рН = 2 в системе наблюдается обратимая агрегация (степень агрегации Т= 1,7). Из расчетов энергии взаимодействия частиц по теории ДЛФО следует, что при концентрациях электролита 1 : 1, превышающих 1 • 10~2 моль/л, на всех расстояниях молекулярные силы преобладают над ионно-электростатическими. Таким образом, наблюдаемое отсутствие агрегации частиц вплоть до концентраций КС1 5-Ю-1 моль/л может быть объяснено тем, что реальная потенциальная «яма» не достигает достаточной глубины, необходимой для образования агрегатов. Это, очевидно, связано с существованием ГС воды у поверхности частиц ПА, что обусловливает возникновение структурной составляющей расклинивающего давления.
При рН = 6 дисперсия ПА в области концентраций КС1 10~3-М0-1 М также устойчива, однако при концентрациях КС1 выше 1,6-Ю-1 М в системе происходит агрегация. Малое значение т (1,3—1,5) соответствует появлению неглубокого минимума при суммировании молекулярной и структурной составляющей.
Интересен обнаруженный факт резкого изменения устойчивости системы при дальнейшем небольшом (от 1,8 до 2-Ю"1 М) повышении концентрации КС1. При этом значительно увеличивается скорость коагуляции и образуются более крупные агрегаты. Уже через 1 ч после начала наблюдения степень агрегации системы составляет 1,9, через 3 ч — 2,7, а через 5 ч — 3,6. При дальнейшем повышении концентрации КС1 до 5-Ю-1 М полученные кривые практически полностью совпадают с зависимостью, найденной для CKci = 2-10_1 М. Резкое изменение поведения системы при данной концентрации КС1 позволяет считать эту концентрацию в определенном смысле пороговой. Вполне вероятно, что именно при этой концентрации (при рН = 6) происходят резкие структурные изменения в ГС, приводящие к частичному или полному их разрушению. Резкое изменение состояния ГС обусловливает возможность большего сближения частиц и, следовательно, реализации более глубокой потенциальной «ямы». Это, в свою очередь, является причиной большей скорости агрегации, образования более крупных агрегатов и возможного изменения характера агрегации. Распад образовавшихся агрегатов становится менее вероятным, не наблюдается выход на плато при выбранном времени наблюдения.
Наблюдения за устойчивостью и коагуляцией дисперсии алмаза в щелочной области (рН = 9) проводились непрерывно в течение 6—7 ч и далее через 24 ч. Исходная дисперсия алмаза при рН = 9 без добавления КС1 и при его концентрации 5-Ю-3 моль/л является агрегативно устойчивой. Из расчета энергии взаимодействия по теории ДЛФО следует, что устойчивость дисперсии алмаза при концентрации KClsc;10~3 М обусловлена наличием высокого энергетического барьера (х 160 kT) и очень малой глубиной дальнего минимума. При концентрации К. С1 1-Ю-2 моль/л в системе уже наблюдается заметная агрегация; степень агрегации составляет 2,7. При дальнейшем росте концентрации КС1 увеличивается скорость и степень агрегации, достигнутая к определенному времени наблюдения. Это связано с постепенным уменьшением вклада ионно-электростатической составляющей и реализацией более глубокой потенциальной «ямы». Обратимый характер агрегации в случае средних концентраций (10-2, Ю-1 моль/л), возможно, связан с влиянием структурной составляющей энергии взаимодействия, что приводит к ограниченности глубины «ямы». Однако в целом агрегативная устойчивость и коагуляция дисперсии алмаза при рН = 9, в отличие от рассмотренных выше случаев, может быть объяснена теорией ДЛФО в ее классическом варианте.
Из приведенных данных по исследованию устойчивости дисперсии алмаза в растворах К. С1 следует, что в зависимости от рН дисперсионной среды и концентрации электролита и, как следствие этого, от состояния поверхности дисперсия алмаза ведет себя либо как лиофилизованная (кислая область), либо как ионно-стабилизированная (щелочная область) дисперсная система, обнаруживая тем самым различную чувствительность к добавлению индифферентного электролита. В зависимости ог состояния поверхности частиц алмаза (соотношения числа диссоциированных и недиссоциированных поверхностных групп), возможности образования водородных связей между молекулами воды и поверхностными группами алмаза, а также от концентрации добавленного электролита меняется структура воды в ГС, и, как следствие, соотношение между молекулярной, ионно-электростатической и структурной составляющими энергии взаимодействия частиц.
Обращает на себя внимание антибатный характер зависимости ^-потенциала и устойчивости системы от рН: с ростом рН по мере возрастания электрокинетического потенциала устойчивость системы уменьшается. Аналогичные результаты получены в работах [502, 503] при изучении электрофоретического поведения и устойчивости дисперсии Si02.
Для выяснения влияния природы иона электролита на устойчивость дисперсии алмаза в растворах LiCl, CsCl и ВаС12 в широком интервале рН (2—9) и концентраций (Ю-3— 5-Ю’1 моль/л для LiCl и CsCl и 5-Ю-5—5-Ю-2 моль/л для ВаС12) получены зависимости обратной счетной концентрации частиц 1 /п от времени T. Влияние исследованных катионов на коагуляцию дисперсии алмаза различно. При концентрации выше 1-Ю-2 моль/л значения ^-потенциала алмаза в растворах LiCl, КС1 и CsCl существенно не различаются. Следовательно, и результаты теоретических расчетов энергии взаимодействия частиц на основании классической теории ДЛФО, и ожидаемые степени агрегации должны быть близки. Наблюдаемое в эксперименте существенное различие в агрегативной устойчивости в растворах хлоридов щелочных металлов может быть объяснено с привлечением представлений о ГС и влиянии их структуры и протяженности на агрегативную устойчивость исследованных систем.
Сказанное выше относится и к объяснению данных, полученных при коагуляции дисперсии алмаза в растворе ВаС12, когда с ростом рН происходит значительное изменение устойчивости системы, несмотря на то, что электростатическая составляющая энергии парного взаимодействия должна изменяться незначительно. По всей вероятности, такой разный характер зависимости устойчивости и электрокинетического потенциала от рН связан не только с присутствием ГС, но и с тем, что их структура и протяженность меняются с изменением рН и концентрации электролита. Последнее предположение подтверждается, в частности, при изучении агрегативной устойчивости дисперсии алмаза при рН = 9. При концентрациях ВаС12 5-Ю-3 и 1-10~2 моль/л степень агрегации т=1,8. Вклад ионно-электро — статической составляющей при этих концентрациях крайне мал, частицы агрегируют в первичной яме ограниченной глубины. Наблюдаемый рост степени агрегации до т = 2,3 при повышении концентрации ВаС12 до 5-Ю-2 моль/л свидетельствует о росте глубины этой ямы, что может быть объяснено уменьшением вклада структурной составляющей вследствие «перестройки» ГС с ростом концентрации электролита.
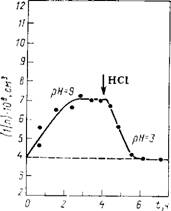
Для демонстрации обратимости процесса агрегации дисперсии алмаза в растворах ВаС12 был проведен следующий эксперимент. К дисперсии алмаза добавляли раствор ВаС12 (1-Ю-2 моль/л) и рН системы доводили до 9, что вызывало
|
Рис. 10.8. Зависимость обратной счетной концентрации частнц алмаза от времени T в Ю-2 М растворах ВаС12 при переходе от рН=9 к рН=3 |
Рис. 10.9. Зависимость степени агрегации т частиц алмаза от времени в
5-Ю-1 М растворе LiCl.
Температура опыта, °С: 20 (/); 40 (2); 50 (3)
Агрегацию частиц: т= 1,8 (рис. 10.8). Последующее введение НС1 (до рН = 3) приводило к полному распаду образовавшихся агрегатов. Поскольку для обоих рН при данной концентрации ВаС12 вклад ионно-электростатической составляющей мал и, кроме того, он должен уменьшаться при подкислении системы, а силы молекулярного притяжения примерно одинаковы, то полученные результаты можно объяснить изменением структуры и ростом протяженности ГС на поверхности алмаза при переходе от рН 9 к рН 3.
Экспериментальные данные по изучению устойчивости дисперсии ПА в растворах различных электролитов не дают однозначного ответа на вопрос о влиянии различных ионов на структурную составляющую. Можно предположить, что механизм образования ГС в присутствии различных ионов достаточна сложен. На сложный характер влияния ионов лиотропного ряда на состояние воды в ГС указано, в частности, в работе [479], где приводятся данные о структурной составляющей расклинивающего давления П5, действующего между гидрофильными кварцевыми пластинками в широком интервале концентраций галогенидов лития, натрия и калия (Ю-1—1 моль/л), свидетельствующие о значительном различии величины максимумов. ns и их положения для ионов лиотропного ряда.
|
|
В исследованной нами дисперсии алмаза структура воды в ГС, по-видимому, определяется как состоянием поверхности частиц алмаза, обусловливающим возможность образования
водородных связей между молекулами воды и поверхностными группами алмаза, так и концентрацией и типом ионов электролита.
Для подтверждения развиваемых представлений о значительной роли ГС воды в агрегативной устойчивости дисперсий гидрофильных частиц было исследовано влияние температуры на коагуляцию дисперсии алмаза. На основании литературных данных [30, 87, 477, 517] можно было ожидать, что с ростом температуры должен уменьшаться вклад положительной структурной составляющей в общую энергию взаимодействия частиц. Это, в свою очередь, должно снижать агрегативную устойчивость гидрофильных или гидрофилизированных дисперсий. Подтверждающее это положение экспериментальные данные, полученные для дисперсии алмаза в 5-Ю-1 М в растворе LiCl при рН = 2 в интервале температур 20—50 °С приведены на рис. 10.9. Незначительная степень агрегации, наблюдаемая при 20 °С (т=1,5), заметно увеличивается при возрастании температуры до 40 °С (т=1,8). Дальнейший рост температуры (50 °С) приводит к изменению самого характера процесса агрегации: значительно увеличивается скорость коагуляции, образуются более крупные агрегаты, отсутствует выход на плато, наблюдавшийся при более низких температурах. При меньших концентрациях электролита (1-Ю-2 М LiCl) влияние повышения температуры становится менее заметным: при 50 °С в дисперсии алмаза наблюдается лишь незначительная степень агрегации.
Результаты исследования устойчивости дисперсии алмаза в растворах LiCl (Ю-2—5-Ю-1 моль/л) при рН, равных 2, 3 и 6, и температуре опыта 20, 40 и 50 °С [25] показали, что с ростом температуры и повышением концентрации электролита устойчивость системы также уменьшается. Аналогично проявляется влияние температуры на устойчивость дисперсии ПА в растворах А1С13.
Все приведенные выше данные о температурной зависимости устойчивости дисперсии ПА свидетельствуют о том, что повышение температуры при постоянной концентрации электролита приводит к частичному разрушению и утончению ГС. При этом появляется возможность сближения частиц, реализации более глубокого энергетического минимума и, следовательно, роста степени агрегации. Тип и концентрация электролита, как обсуждалось выше, в известной мере определяют структуру и протяженность ГС и, следовательно, оказывают влияние на характер изменения степени агрегации частиц ПА с ростом температуры.
Возможность обратимости процесса образования и разрушения ГС при изменении температуры продемонстрирована на рис. 10.10, на котором приведена зависимость обратной счетной концентрации частиц ПА от времени в растворе LiCl при мно-
|
50°С |
|
50" С V ‘ % |
|
ГО Q S y |
|
V 22 °С/ |
|
22 С |
|
О 7 |
I I____ I____ L_
|
25 Ъ,ч |
Ч Є 8 Ю
Рис. 10.10. Зависимость обратной счетной концентрации частиц алмаза от времени при чередовании нагрева (до 50 °С) и охлаждения (до 22 °С) в 5-Ю-1 М растворе LiCl (рН=3)
Гократном изменении температуры (нагрев — охлаждение — нагрев— охлаждение). Как видно из рисунка, небольшая при 22°С степень агрегации (т= 1,2) увеличивается до т= 1,7 при нагреве до 50 °С, что, как уже отмечалось, может быть связано с увеличением глубины потенциальной ямы за счет возможного частичного утончения ГС. Последующее охлаждение (до 22 °С) возвращает систему в первоначальное состояние. Повторный цикл «нагрев — охлаждение» не вносит никаких изменений в наблюдаемую зависимость. Эти данные свидетельствуют об обратимости процесса агрегации, связанной, по нашему мнению, с-полной обратимостью состояния и протяженности ГС в исследованной системе при изменении температуры.
Таким образом, все приведенные здесь данные по исследованию дисперсий кварца, аморфного кремнезема и природного алмаза в водных растворах ряда электролитов при различных значениях рН показывают значительную, а в большинстве случаев — определяющую роль структурной составляющей в устойчивости гидрофильных дисперсий. Структурная составляющая энергии взаимодействия частиц определяется не только природой вещества частиц, но в значительной степени зависит от рН, температуры, концентрации и типа электролита.
 24 октября, 2012
24 октября, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике 