В. Я. Антонненко, В. В. Ильин, Н. Н. Маковский (Институт теоретической физики АН УССР, Киев)
Известно, что характер протекания ряда важных физических и химических процессов на границе ‘раздела фаз в жидкостях отличается от наблюдаемого в объеме, вне действия поверхностных сил. Эти отличия, как показывают экспериментальные исследования [42], в значительной степени обусловлены изменением структурных характеристик жидкостей в приповерхностной области. Вместе с тем однозначная интерпретация экспериментальных данных о свойствах жидкостей вблизи границы часто осложняется влиянием неконтролируемых факторов. Для разрешения ряда проблем физики поверхностных процессов необходимо развитие микроскопической теории приповерхностных слоев жидкости.
Для практических приложений особый интерес представляет исследование водных систем. Вода является сложным объектом для теоретического рассмотрения вследствие особого характера взаимодействия между ее молекулами. Квантовомеханические расчеты показывают, что гибридизация 2S— и 2р-орбиталей атома кислорода при образовании молекул воды обусловливает появление отрицательно заряженных областей, которые расположены симметрично относительно плоскости молекулы. Эти области, в которых распределяется отрицательный заряд атома кислорода, называют гибридизованными неподеленными парами [334]. Такое распределение зарядов в молекуле воды приводит к тому, что каждая молекула может образовать четыре направленные межмолекулярные водородные связи.
Отличительной чертой воды по сравнению с большинством, других жидкостей является содержание ионов оксония и гидро — ксила — продуктов диссоциации молекул воды. Концентрация этих ионов мала и составляет величину порядка 10^7 моль/л. Однако большая подвижность этих ионов по сравнению с примесными ионами приводит к тому, что их влияние необходимо- учитывать в ряде процессов. Так, идеально очищенная вода должна проявлять слабую электропроводность.
Таким образом, кроме общих закономерностей, присущих всем жидкостям, в воде проявляются эффекты, связанные с анизотропией потенциала межмолекулярного взаимодействия и присутствием ионов оксония и гидроксила. Эти особенности должны быть учтены при изучении молекулярно-статистических свойств воды.
Трудности описания свойств жидкостей в рамках микроскопического подхода известны [335]. В первую очередь, они связаны с тем обстоятельством, что, несмотря на сильные межмолекулярные взаимодействия, для жидкостей характерна только — локальная пространственная упорядоченность. Кроме того, развитые в статистической теории жидкостей аналитические методы не всегда позволяют из-за математических трудностей рассмотреть свойства жидкостей, потенциал межмолекулярного- взаимодействия которых анизотропен. Поэтому наиболее прямым путем получения информации о свойствах водных систем в рамках статистической физики является вычислительный эксперимент. Рассмотрим его основные положения. Среднее значение некоторой величины А, которая характеризует состояние системы из N частиц, определяется следующим образом:
<Л>= S A(qlt q2, …, qn)SN(qb q2………………………………. qN) X
X dqi, dq2, …, dq„. (7.1)
Здесь Qi ■— координата і-Й частицы; 0 ,………………………. ч ____________ Ехр[ —UN(qi, д2 Як)!кТ}
………………….. Г -и Ніч і, Яг,…, on) 1 , . . • (7’2>
I Ехр ——————————————- jpjn———— «?1, dq2,…, dqN
Где <72,…, qn)—потенциальная энергия системы; Т — температура и
K — постоянная Больцмана.
В статистической физике для вычисления средних значений <Л> по выражению (7.1) используют коррелятивные функции, которые определяются системой N интегро-дифференциальных уравнений (см., например, [335]). Этот подход позволяет получать точные решения только для простейших одномерных систем, в более сложных случаях приходится использовать упрощающие допущения. Поэтому были развиты методы, позволяющие осуществить прямое вычисление (7.1). Наиболее простой путь заключается в использовании квадратурной формулы:
J М
<л>*=~772 Мчи, Ы………………………………………………….. Ят)- (7.3)
Т t=i
Здесь Qu, Qa,.—, Qm — значения координат в узловых точках iV-мерного пространства, которые определяются функцией распределения (7.2). Для вычисления узловых точек используется реализация цепи Маркова [336]. Этот метод называется методом Монте-Карло и состоит из двух этапов. На первом, как правило более трудоемком, генерируется последовательность узловых точек. На втором этапе, используя полученные данные, вычисляют средние значения искомых величин. Значение <Л> соответствует каноническому ансамблю. В ряде задач более удобно использовать другие статистические ансамбли, при этом несколько изменяется процедура определения узловых точек в (7.3). Необходимо отметить, что узловые точки с физической точки зрения представляют собой мгновенные конфигурации равновесной многочастичной системы и поэтому дают информацию, которая недоступна в реальном эксперименте.
Другой подход вычислительного эксперимента в теории жидкостей заключается в интегрировании уравнений движения частиц, образующих систему. Средние значения величины А определяют при этом усреднением по времени, в течение которого рассматривается эволюция системы. Согласно эргодической гипотезе, эта оценка должна совпадать с (7.3). Этот подход называют методом динамики, и к его преимуществу, по сравнению с методом Монте-Карло, следует отнести возможность вычисления транспортных характеристик многочастичной системы. Однако необходимо отметить, что расчеты методом Монте-Карло дают более устойчивые результаты.
В рамках рассмотренных методов при их конкретной реализации с использованием ресурсов современной вычислительной техники даже в простейших случаях удается учитывать порядка 103 частиц. Поэтому с целью исключения граничных эффектов используют периодические граничные условия [336].
Для расчета свойств реальной системы методами вычислительного эксперимента необходимо задать феноменологический потенциал межмолекулярного взаимодействия. В молекуле воды зарядовое распределение аппроксимируется, как правило, то-
Таблица 7.1. Результаты расчета чечными зарядами. Кроме
Характеристик воды в объемной фазе кулоновской энергии взаимо — При 300 К и плотности 1 г см3 J » Ґ
Действия учитываются также короткодействующие силы отталкивания. Обзор используемых в настоящее время моделей молекулы воды дан в работах [337— 339].
Рассмотрим результаты расчета некоторых свойств объемной фазы воды для двух моделей. В модели межмолекулярного потенциала ST2 [340]j используются четыре точечных заряда, расположенных в вершинах тетраэдра. Электростатическое взаимодействие плавно выключается при малых расстояниях между молекулами. Короткодействующие силы отталкивания учитываются потенциалом Леннарда — Джонса 6-12 между атомами кислорода. Дипольный момент молекулы воды равен 2,35 Д, а абсолютный минимум энергии димера воды составляет 28,4 кДж/моль при расстоянии 0,285 нм между атомами кислорода.
Модель межмолекулярного потенциала SPC [338] использует три заряда, расположенных на атомах водорода и кислорода. Так же как и в модели ST2, между молекулами воды действует потенциал 6-12, центрированный на атомах кислорода. Для определенных параметров модели выполнялась серия пробных расчетов с целью минимизировать отклонение рассчитанных величин от данных экспериментальных измерений. В результате получен дипольный момент, равный 2,27 Д, энергия водородной связи равна 27,6 кДж/моль при равновесном расстоянии 0,276 нм между атомами кислорода в димере воды.
В табл. 7.1 приводятся результаты расчета методами вычислительного эксперимента фактора сжимаемости и средней од — ночастичной потенциальной энергии для двух описанных выше моделей воды. Фактор сжимаемости Z по определению равен
Z=P/(9kT), (7.4)
|
Модель |
Z |
КДж/моль |
|
ST2 [3401 |
0,77 |
43,9 |
|
SPC [338] |
—0,36 |
42,2 |
|
Эксперименталь |
Ю-3 |
41,4 |
|
Ные данные |
Где р — давление; р — плотность числа частиц.
|
(7.5) |
Величина средней одночастичной потенциальной энергии определяется в расчете следующим образом:
W = "Ah
Іфї
Где N — число частиц, по которым ведется суммирование; Utj — энергия взаимодействия между t-й и /-й молекулами. Угловые скобки означают усреднение по цепи Маркова, которая генерируется в процессе расчета.
Из приведенных данных следует, что энергетические характеристики находятся в достаточно хорошем согласии с результатами эксперимента, величина же фактора сжимаемости при плотности 1 г/см3 не воспроизводится. Отрицательная величина давления, полученная при использовании потенциала SPC, свидетельствует о том, что система при заданной плотности находится в метастабильном «растянутом» состоянии. То, что это состояние реализуется в течение всего расчета, обусловлено влиянием периодических граничных условий.
На рис. 7.1 для рассмотренных в табл. 7.1 моделей показано распределение вероятности встретить заданное число К ближайших соседей для выделенной молекулы воды. Как видно, эти модели правильно отражают анизотропный характер взаимодействия между молекулами воды: максимум распределений находится при К=4, в соответствии с числом направлений, по которым может образоваться водородная связь.
Полученные методами вычислительного эксперимента результаты позволяют сделать вывод о том, что рассмотренные потенциалы межмолекулярного взаимодействия приводят к качественно правильному описанию свойств воды в объемной фазе. Для того чтобы избежать «растянутого» состояния, достаточно увеличить плотность числа частиц, что слабо сказывается на рассчитанных значениях структурных и энергетических характеристик водных систем. Анализ показывает [339], что это заключение справедливо и для ряда других моделей. Поэтому выбор потенциала межмолекулярного взаимодействия для описания мо- лекулярно-статистических характеристик воды определяется, в основном, минимумом времени, затрачиваемого на расчет энергии взаимодействия в системе. Кроме того, для сопоставления результатов, полученных при различных внешних условиях, необходимо использовать одну и ту же модель.
В работах [2, 341, 342] на основе данных, полученных методами вычислительного эксперимента, была установлена связь между наблюдаемыми в тонких прослойках микроструктурными эффектами и локальной пространственной упорядоченностью частиц простых жидкостей. Для водных систем у поверхности можно ожидать также изменения структуры водородных связей. С целью исследования влияния
Поверхности на структурные и Р(к) __________
Термодинамические характеристики воды были выполнены 0,4 Расчеты для нескольких модельных систем.
Рис. 7.1. Распределение вероятности координационного числа Р(К) в воде Для моделей межмолекулярного потен- 0,0
|
|
Циала ST2 (1) и SPC (2) 0 1 3 5 7 К
|
Таблица 7.2. Термодинамические свойства водных систем (модель Роулинсона)
|
|
* В одномерной системе безразмерная плотность равна ро. |
Для описания межмолекулярного взаимодействия в расчетах методом Монте-Карло использовали потенциал Роулинсона [343]. В модели Роулинсона (RWL) на атомах водорода воды располагаются положительные заряды, отрицательные заряды помещаются на линии, проходящей через атом кислорода перпендикулярно плоскости молекулы. Дипольный момент молекулы в этой модели равен 1,85 Д. Энергия связи димера воды 22,6 кДж/моль при равновесном расстоянии 0,269 нм.
Расчет выполняли для свободной пленки воды и воды, заполняющей цилиндрическую пору с радиусом /? = 0,35 нм. Поверхность цилиндра непроницаема для центров масс молекул воды, но не ограничивает вращательных степеней свободы. Исследовали также изменения свойств воды под влиянием внешней стороны цилиндра. Для этого бесконечно длинные стержни радиуса 0,45 нм располагали в шахматном порядке на расстоянии 1,3 нм между их осями. Пространство между стержнями заполняли молекулами воды, стержни непроницаемы для их центров масс. Такая система моделирует свойства мембранной фазы воды [2]. Расчеты выполняли в каноническом ансамбле при температуре 7 = 298 К.
В табл. 7.2 приводятся результаты расчета энергии (7.5) и теплоемкости при постоянном объеме:
Кроме перечисленных систем был выполнен расчет для объемной фазы воды. При плотности 1 г/см3 жидкость в модели Роулинсона находится в «растянутом» состоянии. Плотность свободной пленки воды составляет 1,3 г/см3, поэтому свойства объемной фазы рассчитывали и при этом значении плотности. Плот
ность в табл. 7.2 приведена в безразмерных единицах т] = = (о=0,264 нм [2]).
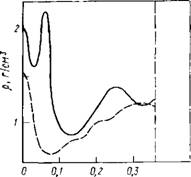
При исследовании свойств пленки воды, находящейся в контакте с поверхностью, на которой расположены активные центры, учитывали не только влияние границы, не пропускающей центры масс молекул, но также и вклад от жестко закрепленных молекул воды, чьи атомы кислорода расположены в шахматном порядке на граничной плоскости. Расстояние между ближайшими атомами кислорода выбиралось равным 0,311 нм. На рис. 7.2 приведены результаты расчета локальной плотности этой системы. Как видно из рисунка, для пленки воды характерна пространственная неоднородность, как и в случае прослойки частиц с жестким кором [341]. Полученные результаты позволяют утверждать, что пространственная неоднородность в приповерхностных слоях жидкости обусловлена влиянием поверхности.
|
|
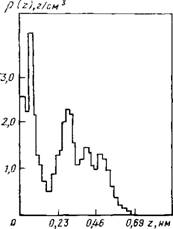
Из данных, приведенных в табл. 7.2, следует, что искажение сетки водородных связей значительно сильнее в цилиндрической поре по сравнению с плоской. На рис. 7.3 приведены результаты расчета локальной плотности вдоль оси цилиндра. Как видно, при плотности г] = 0,42 система разделяется на капли. Для сплошного заполнения цилиндрической поры необходимо увеличить плотность, но и при г| = 0,54 результаты расчета указывают на сохранение пространственной неоднородности вдоль оси ци-
|
|
Рис. 7.2. Локальная плотность воды у поверхности с активными центрами
Рис. 7.3. Локальные плотности молекул воды вдоль оси цилиндрической
Поры:
Рср—1.3 г/см3 (/) и 1 г/см3 (2)
|
|
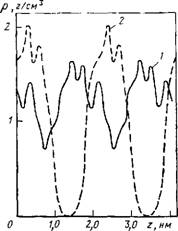
Рнс. 7.4. Радиальные распределения локальной плотности для воды в цилиндрической поре
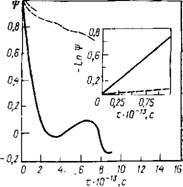
Рис. 7.5. Автокорреляционная функция скорости Т.
Пунктирная линия соответствует неограниченному направлению, сплошная — ограниченному
Линдра. Приведенные на рис. 7.4 радиальные распределения локальной плотности показывают, что ее величина возрастает при приближении к поверхности. Такая зависимость обусловлена особенностями оптимальной упаковки частиц в цилиндрической поре и согласуется с результатами расчета для систем частиц с жестким кором [344].
Изучение транспортных характеристик молекул воды в пленках представляет особый интерес. С этой целью выполняли расчет методом молекулярной динамики, в котором для описания межмолекулярного взаимодействия использовалась модель BNS [340]. Выбор этой модели связан с тем, что в ее рамках подробно исследовались свойства воды в объемной фазе [339]. В процессе расчета температуру системы поддерживали равной 306 К-
Характеристикой коллективного движения частиц в жидкости является автокорреляционная функция скорости:
Т(т) <»> • (7-7>
Здесь т — время, v — скорость частицы. Угловые скобки означают усреднение по времени и по частицам в системе.
|
|
На рис. 7.5 показаны зависимости автокорреляционных функций скорости от времени для ограниченного направления и направлений, по которым накладываются периодические граничные условия. Автокорреляционная функция скорости, соответствующая движению частиц поперек пленки, имеет осциллирующий характер, что связано с ограниченностью системы. При
малых интервалах времени (порядка Ю-13 с) автокорреляционная функция скорости, как следует из результатов расчета, хорошо аппроксимируется экспоненциальной зависимостью. В этом случае оценка времени затухания приводит к значению 9,5- • 1(Н3 с — для неограниченного направления и 1,4-Ю-13 с— для ограниченного. Из приведенных данных следует, что для тонких пленок воды характерна анизотропия подвижности молекул. Расчет коэффициента самодиффузии D вдоль неограниченного- направления с помощью соотношения Эйнштейна приводит к значению 2-Ю-3 см2/с. Это существенно выше результата расчета для объемной фазы [340] D = 4,2-10~5 см2/с, что связано со — значительным вкладом от подвижных молекул на свободных границах тонкой пленки.
Для исследования изменений структуры водородных связен в приповерхностных слоях воды необходимо проанализировать ориентационные характеристики ее молекул. Ориентация молекул может быть задана углами Эйлера. Однако для большей наглядности целесообразно рассмотреть ориентацию в пространстве вектора р, дипольного момента молекулы воды и вектора п, нормального к плоскости, в которой расположены атомы молекулы. Введем параметр порядка
Где <cos20> — среднее значение квадрата косинуса угла между вектором, определяющим ориентацию частицы в пространстве (п или ц) относительно-
Выбранного направления.
Из (7.8) следует, что при ориентации всех частиц строго нормально к выбранной оси параметр порядка s равен единице. Если же векторы расположены перпендикулярно этой оси, то — s = —0,5. В том случае, когда распределение направления векторов случайно, s = 0. В табл. 7.3 приведены рассчитанные значения параметров порядка sn для вектора п и sM — для вектора р,. относительно направления, нормального к поверхности.
Из данных табл. 7.3 следует, что вблизи поверхности (независимо от ее кривизны) структура водородных связей искажается таким образом, что система приобретает ориентационную — упорядоченность. Плоскости молекул воды расположены преимущественно параллельно ограничивающей поверхности в данной точке. Для пленки воды у поверхности с активными центрами значения средних по толщине ориентационных характеристик согласуются с данными для пленок со свободными границами. Более детальный анализ показывает, что отличия в ори — ентационной упорядоченности молекул проявляются только в пределах первого монослоя у поверхности — там, где молекулы жидкости могут образовывать водородные связи с активными центрами.
Результаты расчета термодинамических характеристик одномерной
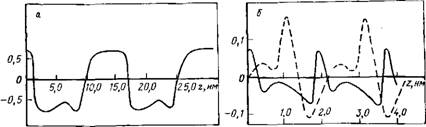
Системы молекул воды (см. табл. 7.2) показывают, что здесь преобладают силы притяжения между молекулами, несмотря на значительное увеличение энергии по сравнению с объемной фазой. Из результатов расчета, приведенных на рис. 7.6, а, видно, что в системе реализуется ориентация «голова к хвосту». Так как в одномерной системе полное упорядочение невозможно, система разделяется на кластеры молекул с одинаково ориентированными дипольными моментами.
На рис. 7.6,6 показано распределение значений дипольного момента молекул воды в цилиндрических порах. Дипольные моменты ориентируются преимущественно параллельно оси цилиндра, так как в отличие от плоских пленок эта ось является дополнительным выделенным направлением. Этот эффект приводит к электростатическому отталкиванию между образовавшимися каплями, что усиливает тенденцию к пространственному разделению системы.
|
Таблица 7.3. Ориентационная упорядоченность молекул воды в ограниченных водных системах относительно направления, нормального к поверхности
|
Ориентационные характеристики молекул воды в мембранной фазе рассматривались относительно направления, параллельного осям стержней, ограничивающих движение центров масс молекул воды. Результаты расчета приведены в табл. 7.4 для приповерхностного слоя толщиной 0,075 нм. Как видно из этих данных, в модели мембранной фазы воды также наблюдается ориентационная упорядоченность ее молекул.
|
|
|
Hz/V |
|
WM |
|
Рис. 7.6. Распределение проекции вектора поляризации вдоль одномерной цепочки молекул воды (а) и вдоль цилиндрической поры, заполненной водой (б) |
Эффект ориентацион — ной упорядоченности молекул воды в приповерхностной области устойчив по отношению к внешним воздействиям. Этот вывод подтверждается как исследованиями молекулярно-стати — стических свойств пленок воды у поверхности с активными центрами, так и изучением влияния внешнего» электрического однородного поля [345]. Отметим, что ориен — тационная упорядоченность молекул жидкости наблюдается к в других системах. Так, экспериментальные исследования [42] показали, что нитробензол на границе твердого тела образует протяженную жидкокристаллическую фазу.
Каковы возможные следствия упорядоченности водных систем под влиянием границы? Известно, что жидкость, которая находится в контакте с поверхностью, становится неоднородной (см. рис. 7.2). Рассмотрим унарную функцию для жидкости, ограниченной плоской поверхностью:
Здесь х — расстояние от границы; ф(д:) —потенциал средней силы. Тогда для плоской прослойки с толщиной Н унарная функция в суперпозиционном приближении может быть представлена следующим образом:
Л<«, + ]. (7.10).
Из (7.10) следует, что локальная плотность в жидкой прослойке изменяется по закону
Pl(*, Я) =-^р1°(*)Рі<)(Я-*), (7.11)»
Где рь — плотность числа частиц в объемной фазе; рі°(*)—локальная плотность числа частнц в системе с одной границей.
В случае идеальных границ прослойки давление определяется контактным значением локальной плотности:
-Јjr t= Pl(* =я 0, Н) *= Pl(* Я, Н) ^ ЯрДЯ). (7.12у
|
Таблица 7.4. Характеристика ориентационной упорядоченности молекул воды в ограниченных водных системах
|
Влияние фактора сжимаемости Z определяет условие равновесия жидкости в прослойке с объемной фазой в приближении (7.10). Используя представление функции рі°(л;) в асимптотиче-
ской области [346], получим оценку вклада пространственных микроструктурных эффектов в поверхностные силы: Ns(H)
« ехр( — <xH)cos(wH + б), (7.13)
Тде jts — величина избыточного давления на границы прослойки.
Вклад (7.13) может проявляться и в простых жидкостях, и в такой сложной ассоциированной жидкости, как вода. Эффекты структурных сил подтверждаются экспериментальными данными [347, 348]. Формула (7.13) является асимптотической. Результаты более полного исследования природы поверхностных сил, проявляющихся при изменении пространственной микроструктуры жидкости под влиянием поверхности, приведены в работах 1341, 349, 350].
Рассмотрим связь между ориентационной упорядоченностью молекул в прослойке и силами, действующими на ее границе. Ограничимся случаем, когда средняя плотность частиц в прослойке изменяется в зависимости от ее толщины по следующему закону [351]:
2Г
P«=P6 + "7jr. (7.14)
Где Г — величина адсорбции.
При условии (7.14) влиянием пространственных микроструктурных эффектов можно пренебречь. Тогда, если выделить часть свободной энергии F‘, соответствующую вкладу ориентационной упорядоченности системы, найдем дополнительный вклад в силы, действующие на границы прослойки:
А___________________________ 1 д ( F’
KT " W дН KT
(7.15)
|
IL W |
R=const
Где w — площадь поверхности.
Влияние избытка свободной энергии F‘ неоднородной ориен — тационно упорядоченной системы может быть оценено в приближении Ван-дер-Ваальса (см., например, [352]). В работе [353] ■было показано, что в том случае, когда величина параметра порядка на границах прослойки удовлетворяет условию
S(x=0) >s(x=H)=su (7.16)
Избыток свободной энергии F‘ равен
S1 ____________________
•= [t(Si)// + 4 f V-c(s) — t(s0)dsj. (7.17)
So
Здесь T(S) определяет плотность свободной энергии в объемной фазе при заданном значении параметра порядка S. Вели
чина sо соответствует значению параметра порядка в центре прослойки и определяется уравнением
S1
Ds
|
Exp 0, При|хг-х/|< "I", |Si-Sjl<-jT-. V1 * VJ |
(7.18)
W
/т(з)—фо) • So
Подставляя (7.17) в (7.15), найдем:
Яа (H)=X(S0). (7.19)
Из табл. 7.3 видно, что значение параметра порядка Sn в тонких пленках воды мало по сравнению с характерным значением для фазового перехода в объемной фазе анизотропных жидкостей. Поэтому для анализа зависимости (7.19) от толщины прослойки можно воспользоваться при определении плотности свободной энергии приближением Ландау — де Жена:
—C(S) =as2. (7.20)
Тогда из (7.18), (7.19) и (7.20) следует:
*а(Я) 1 п 2П
KT ~ сЬ2(лаЯ/2) ‘
Где 1 /г—параметр, имеющий размерность длины.
Так как условие (7.14) выполняется при больших значениях толщины прослойки, перейдем в (7.21) к асимптотическому представлению:
Яа (Щ/kT ~ ехр (ГаЯ). (7.22)
Качественно зависимость (7.22) подтверждается экспериментальными данными [41, 42].
Для изучения влияния ориентационной упорядоченности молекул на приповерхностные силы без введения условий (7.14) рассматривалась следующая модельная система. На плоскости размещали нити конечной длины L, для них допускалась возможная ориентация в двух взаимно перпендикулярных направлениях. Эти частицы совершают поступательное движение на плоскости, причем потенциал взаимодействия между ними определен следующим образом:
— Я frj ~rh vt vj) "1
KT J^
.. v
<ґ — . Vt Ф V,
(7.23)
1, прн обратных условиях
Где ri — вектор, определяющий положение центра масс 1-й частицы; vi — параметр, характеризующий ее ориентацию.
Поскольку возможны только два направления ориентации, определим, что в одном из них находится Ni частиц и Nц — в другом. Введем параметр порядка в этой системе частиц:
N1 — Ni
(7-24)
Тогда свободная энергия системы, связанная с ориентацион — ной упорядоченностью, равна [354]:
-fir — 4" [ (1 + s)’n(I +«) + (»- s)In( I — s) ] — S DN(s)s"-K (7.25)
Вириальные коэффициенты в (7.25) до седьмого включительно могут быть определены с помощью одномерных интегралов, приведенных в работе [355]. Их значения приведены в табл. 7.5.
Значение параметра порядка при заданной плотности определяется из решения уравнения:
|
= 0 |
Д ( F Ds KT
(7.26)
Из (7.25) с учетом всех членов разложения согласно табл. 7.5 следует, что при sL2<2,48 уравнение (7.26) имеет только одно решение: s = 0. При большей плотности числа частиц в системе ПОЯВЛЯЮТСЯ дополнительные решения Sm И —Sm, ПрИЧЄМ ОНИ СО — ответствуют минимуму свободной энергии (7.25). Фазовый переход при плотности SL2 = 2,48 — переход второго рода, поэтому полученное в рамках самосогласованного поля решение может оказаться некорректным. Отметим, что рассматриваемая модель близка к модели проницаемых сфер, рассматриваемой в [352] с целью изучения критических явлений.
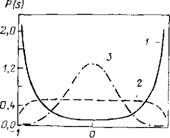
Для учета вклада флуктуаций в свойства системы вблизи критической точки проводили расчет методом Монте-Карло в большом каноническом ансамбле. На рис. 7.7 показаны результаты расчета распределения параметра порядка при различных значениях плотности. Видно, что вблизи точки фазового перехода флуктуации параметра порядка велики и величина парамет-
|
Таблица 7.5. Выражения для вириальных коэффициентов в разложении (7.25)
|
|
Ti s |
Рис. 7.7. Плотность распределения вероятности параметра порядка P(S) Для различных плотностей: pL2=4,5 (/); 3,4 (2); 1,9 (3)
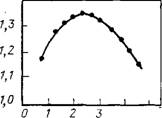
Рис. 7.8. Зависимость фактора сжимаемости от плотности в системе жестких тонких стержней конечной длины
Ра порядка в этой области однозначно не определена. Поэтому воспользуемся определением давления р в виде вириального разложения:
JL. =» р — 2 (п — 1 )Z>„(s)p*. (7.27)
Из (7.27) с учетом данных табл. 7.5 следует, что при отклонении значения параметра от нулевого уравнение состояния приближается к уравнению состояния идеального газа. На рис. 7.8 приведены результаты расчета зависимости давления от плотности числа частиц в системе. Эти данные показывают, что точка фазового перехода согласуется с оценкой в приближении (7.25).
То, что система нитей при плотности числа частиц больше критического значения приближается по своим свойствам к идеальному газу, позволяет ожидать, что при ограничении движения центров масс частиц в этих условиях основной вклад в поверхностные силы будут давать ориентационные эффекты. Ниже приведены результаты расчета для модели прослойки, в которой движение центров масс нитей ограничивалось параллельными линиями на расстоянии Н друг от друга независимо от их ориентации. Расчеты проведены для ограниченных систем нитей при £2рехр [ц7(АЛ] = Ю. Ориентационная упорядоченность системы характеризуется величиной <s2>, которая отражает также характер флуктуаций параметра порядка.
TOC o "1-3" h z H/L оо 5 2
<s2> 0,65 0,42 0,43
PL2/ (kT) 5,18 4,41 4,55
PL2 4,5 4,35 4,4
|
P/pkTJ 1Л |
|
4 J>L* |
Из этих данных следует, что в рассматриваемой системе ориентационная упорядоченность уменьшается в прослойке по срав
нению с равновесной объемной фазой. При этом давление на границе прослойки меньше объемного давления [в отличие от (7.22), где давление на границы прослойки больше объемного].
Как уже отмечалось, подвижность ионов оксония и гидрокси — ла аномально высока по сравнению с примесными ионами. Перенос этих ионов обусловлен транспортом протона по цепочкам молекул воды, связанных водородными связями. Для объяснения этого процесса предложены коллективный механизм Грот — куса и основанный на рассмотрении перехода частицы через барьер механизм Эйринга. В работе [356] рассмотрен механизм переноса протона в водных системах, связанный с коллективным возбуждением солитонного типа. Этот механизм в значительной степени зависит от стабильности проводящей протон цепочки молекул воды. Выполненный анализ [349, 350] показывает, что в приповерхностной области более прочные водородные связи образуются вдоль направлений, параллельных границе. Поэтому можно ожидать, что вклад транспорта протонов в поверхностную проводимость водных систем будет существенным.
Приведенные здесь результаты исследования свойств воды вблизи границы могут служить теоретической основой для интерпретации экспериментальных данных и дальнейших теоретических предсказаний.
 24 октября, 2012
24 октября, 2012  admin
admin 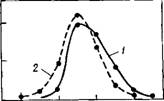
 Опубликовано в рубрике
Опубликовано в рубрике 