Случай сильно искривленных граничных поверхностей принципиально отличается от уже разобранных случаев плоских и слабо искривленных поверхностей.
При рассмотрении сильно искривленных поверхностей наиболее интересной представляется центральная часть капиллярной системы —внутренняя область капли, поры или полости адсорбента и т. п. Именно здесь, помимо молекулярных корреляций и эффектов взаимного возмущения самой капиллярной системы и прилегающего к ней тела (создающего поле поверхностных сил), необходимо учитывать также эффекты перекрытия поверхностных областей. Исследование центральной части капиллярной системы мы проведем в предположении, что радиус кривизны поверхности раздела все же велик по сравнению с молекулярными^размерами.
{Поскольку вид получаемых соотношений в значительной степени зависит от формы поверхности раздела, мы рассмотрим
лишь два наиболее характерных случая: цилиндрическую и сферическую капиллярные системы.
Начнем с цилиндрической капиллярной системы. Расчет функций распределения такой системы в окрестности ее оси симметрии дает формулу [26, стр. 182]:
Р м = р<«> W + I^fjl a-l+3 X
Здесь ск = п — для обычных дисперсионных сил (Я = 6) и С% = 2 — для дисперсионных сил с запаздыванием (Я = 7).
Радиус цилиндрической граничной поверхности а теперь принимает только положительные значения. Индекс же а относится к гипотетической объемной фазе при заданных значениях химических потенциалов. Такая фаза в действительности не реализуется даже в центральной части капиллярной системы из-за большой кривизны поверхности раздела.
В формуле (53) как главный член порядка так и по
Правочный член порядка а~к+2 не зависят от положения молекулярного комплекса {/г} относительно оси. Зависимость от расстояния г комплекса до оси появляется лишь в величинах ОЛ(а~х+Зг21а2) и 0 (а~к+2г2/а2), которыми пренебрегают в рассматриваемой центральной части комплекса, где г! а 1. По отношению к ней радиус а, таким образом, играет фактически роль расстояния от граничной поверхности. В формуле (53) также пренебрегается величинами 0 (a-
Отсутствие в формуле (53) членов порядка и
А-ь+2г/а является следствием симметрии задачи.
Наличие данной симметрии позволяет в то же время дополнительно не симметризировать функцию распределения р [п Отражением в точке внутри комплекса {я}, как это необходимо было делать в формулах (39) и (43).
С помощью (53) можно получить формулы и для других локальных величин в окрестности оси симметрии цилиндрической
|
X |
|
X |
Капиллярной системы. Приведем здесь лишь формулу для локального состава [26, стр. 182]
Х — *«*> + 2яс У A —i—
«. t
X + (54)
S, t
И формулу для локального тензора давлений Р —для его нормальной составляющей Рп [26, стр. 182]
Р _р(«) , Яс (А-5) 11 ь+з ИП~и (X — 2)!! а
|
X |
|
S. / |
A^i (1-2-^+2)] P<«>pj«> +
|
2-^+2p(P)p(P)| + |
|
2 — |
|
+ |
1 (J _ o<a)0(p) — 1
Ria)
|
(55) |
1 o—X,+2n(P)l X — 2 Ps J ‘
И тангенциальной составляющей Ptt вдоль параллельного оси направления [26, стр. 182]:
|
X |
|
(X 2) ! 1+^(1-2^+2) |
|
2"- |
|
X |
|
S. t |
Р — р(а) , лс (Я — 5) !! Л+3 А —2)!!
P<a)pia) +
+ 2 F1 — (1 — 2~*+3>] — ^ + + -^hr 2 ч2 [1" 0 " 2"+2)] —
S. t V
|
(56) |
|
Я — 2 |
1 2-A.+3 p(p)| r(ap)
Что касается второй тангенциальной составляющей Ptt Вдоль перпендикулярного оси направления, то она [это видно, например, из условия механического равновесия (47)] совпадает с Рп в принятом приближении.
Как и в самой формуле (53), в формулах (54)—(56) пренебрегают величинами 0 (а~к+3г2/а2), 0 (а~к+2г2/а2) и 0 (а_я,+1).
Если, в частности, роль создающего поле поверхностных сил тела играет адсорбент, а значения химических потенциалов в адсорбате заданы, то формулы (53)—(56) описывают зависимость соответствующих локальных величин вблизи оси цилиндрической поры от радиуса поры а. Это отвечает обычным условиям эксперимента, когда на поверхности адсорбента, соприкасающегося со средой (с заданными химическими потенциалами), имеется ряд пор различного размера и требуется найти распределение свойств по размерам пор.
Аналогично рассматривается случай сферической капиллярной системы. Для функций распределения данной системы в окрестности ее центра симметрии имеем [24; 26, стр. 182]:
Р {.) — Р№ м + х^з 2 ^[PJw — РН +
TOC o "1-3" h z S, t "S
+ (57,
(a —радиус сферической граничной поверхности).
Благодаря симметрии задачи функции распределения не зависят в принятом приближении от расстояния г до центра сферической системы и эти функции не нужно симметризиро — вать отражением в точке внутри комплекса п. Зависимость функций распределения от расстояния г появляется лишь в членах порядка а—Л+3гя/аа и агк+2г2/а2. Однако этими членами, так же, как и членами порядка в формуле (57) пренебре-
Гается. По отношению к рассматриваемой центральной части системы радиус а может фактически пониматься как расстояние от граничной поверхности.
Формула (57) позволяет найти любую локальную величину в окрестности центра сферической капиллярной системы. Приведем лишь выражение для локального тензора давлений. В случае сферически симметричной задачи тензор давлений в окрестности центра симметрии будет [как в этом легко убедиться, например, с помощью условия механического равновесия (49) ] пропорционален единичному тензору. Последнее означает, что тензор давлений сводится к одной составляющей—
локальному давлению Р. Выражение для локального давления Р имеет вид [24; 26, стр. 182]:
|
|
(58)
В формуле (58) пренебрегают такими же по порядку величинами, как и в формуле (57).
В последнее время Сторонкин и один из авторов настоящей статьи вычислили [32, стр. 163] локальную плотность в центральной части капли и на основе макроскопической теории. Найденная в главном асимптотическом члене для обычных дисперсионных сил без запаздывания зависимость локальной плотности от радиуса капли совпадает с приведенной выше. Сопоставление коэффициентов в соответствующих асимптотических членах дает однозначный рецепт построения парного эффективного потенциала в случае, когда одна из взаимодействующих молекул находится в центральной части капли, а другая — в окружающей каплю среде.
Качественно поведение локальной плотности и локального тензора давления в центральной части малой системы, даваемое приведенными выше формулами (уменьшение плотности и давления с размерами системы), было подтверждено недавно результатами прямого численного эксперимента для малой капли, полученными методом молекулярной динамики [38].
 1 января, 2013
1 января, 2013  admin
admin 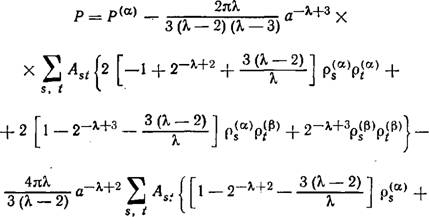
 Опубликовано в рубрике
Опубликовано в рубрике 