В качестве пленкообразующих веществ в основном широко применяются высокомолекулярные соединения. Молекулы высокомолекулярных соединений состоят из многократно повторяющихся структурных единиц (звеньев), соединенных между собой ковалентными связями.
Количество повторяющихся (мономерных, элементарных) звеньев х в макромолекуле может быть велико, поэтому вещества, состоящие из макромолекул, называют полимерами (по гречески полус — много, мерос — доля). Если для реакции взяты два (или более) разных мономера, то полученный продукт будет содержать повторяющиеся звенья различных типов и называется сополимером (совместным полимером).
Поскольку молекулярная масса полимера М составляется из суммы молекулярных масс т всех звеньев, входящих в молекулу полимера, можно записать, что М—тх. Величина х называется степенью полимеризации. В том случае, когда х имеет сравнительно небольшую величину, продукты полимеризации называют олигомерами (по гречески олигос — немного). Между ними и полимерами нельзя провести границу, но верхним пределом для олигомеров можно считать такую их молекулярную массу, при которой начинают проявляться свойства, присущие только полимерам, например высокоэластическая деформация.
В науке о полимерах рекомендуется применять два основных термина — молярная масса и относительная молекулярная масса (молекулярный вес). Молярная масса М — это масса вещества, деленная на его количество в молях (кг/моль, г/моль). Молекулярный вес (относительная молекулярная масса Мг) — отношение средней массы вещества к ’/12 массы ядра атома углерода 12С. Применительно к полимерам молярную массу целесообразно выражать в г/моль, поскольку при этом ее численное значение и значение относительной молекулярной массы вещества совпадают, что дает возможность использовать единый символ М.
Относительная молекулярная масса является безразмерной величиной. В процессе синтеза полимера происходит последовательное присоединение мономеров к растущей полимерной цепи. Кроме того, во многих случаях возможно протекание реакций активной полимерной цепи не только с мономером, но и с образовавшимися в реакционной системе олигомерами и полимера-
Ми. Такие реакции являются вероятностными, поэтому образующиеся макромолекулы различаются длиной цепей. Следовательно, х является усредненной величиной, характеризующей смесь макромолекул различных размеров (полимергомологов). Молекулярная масса полимера также является усредненной величиной молекулярных масс всех полимергомологов, т. е. средней молекулярной массой (весом).
Таким образом, даже химически чистый полимер (например, полиэтилен) не является индивидуальным химическим веществом в общепринятом смысле, а представляет собой смесь полимергомологов с различной степенью полимеризации.
Поскольку полимергомологи различаются по размерам (по молекулярным массам), полимеры можно характеризовать степенью полидисперсности. Менее распространено понятие о степени полимолекулярности полимеров, хотя термин полимолекуляр- ность более правилен, так как в этом случае свойства полимеров рассматриваются на молекулярном уровне. Степень полидисперсности можно охарактеризовать количественно.
Поскольку молекулярная масса полимера является усредненной величиной, ее численное значение зависит от способа усреднения.
Если принимать статистическую массу молекул каждого размера равной их мольной доле Ni|HNi, то в результате усреднения будет получена средне — — числовая (среднечисленная) молекулярная масса М„:
Л/, N. N1 ЕА’гМ;
TOC o "1-5" h z Мп=>М, — + М2——————- —+…+Мг—— =*—————— , (1.1)
1 2#г 2 2Д’г 2ДГг ’ у ‘
Где N1, N2………… N1 — число молекул с молекулярными массами соответственно
Ми М2………. М,.
Следовательно, величина Мп равна отношению массы полимера к общему числу молекул, входящих в его состав.
В том случае, когда статистическую массу каждого вида молекул принимают равной массовой доле молекул данного размера, получают среднемассовую молекулярную массу Мш:
„ „ А, , .. N^1 Ш1№1
Ш 1 2ЛГгМг 2 2ЛГгМг ’ ‘ ‘ ‘ 1 2ЛГгМг ^ 2ЛГгМг ‘ *
Для определения среднечисловой молекулярной массы Мп применяют методы, пользуясь которыми, можно измерить коллигативные (зависящие от числа частиц) свойства растворов: осмометрию, эбуллиоскопию, криоскопию, изотермическую перегонку, измерение тепловых эффектов конденсации, количественное определение концевых групп. Величины среднемассовой молекулярной массы Мю определяют методами светорассеяния и приближения к седиментационному равновесию (ультрацентрифугальный метод).
Молекулярную массу М можно определить и косвенным методом, например вискозиметрическим. В этом случае измеряется характеристическая вязкость раствора полимера, связанная с молекулярной массой определенным соотношением. Получаемая при этом средневязкостная молекулярная масса М-о составляет
ЛГ0=.[2ЛГгМга+1/(2Л’гЖг)]1/°, (1.3)
Стемы полимер — растворитель и при определенной температуре), находящаяся в пределах 1>а>0,5. При а= 1 справедливо равенство Aft, = Afa..
Величина М„ обычно ближе к Д1=, чем к М„. Чем больше разница между значениями Ма и М„, тем больше полидисперсность (неоднородность по — лимергомологического состава) полимера. Поэтому отношение М-Л.1М„ можно условно принять за меру полидисперсности полимера: чем оно ближе к единице, тем однороднее полимер по молекулярным массам.
Одним из методов практической оценки значения полндисперсности полимера является использование фактора неоднородности V= (MwIMn)—1. Обычно для любого полимера МШ>М„, и только в предельном теоретическом случае, при монодисперсности, т. е. при одинаковой молекулярной массе всех макромолекул, Ma,=Af„, и тогда 17=0.
Для подробной характеристики полимера нужно изучить распределение макромолекул по молекулярным массам. Это распределение характеризуется кривыми молекулярно-массового распределения ММР, которым соответствуют функции молекулярно-массового распределения. Для экспериментального построения кривых распределения образец полимера делят на фракции, представляющие собой смесь полимергомологов с относительно близкой степенью полимеризации, и определяют их молекулярные массы. Получаемые значения молекулярных масс являются дискретными. Однако экспериментальные кривые описывают непрерывными, а не дискретными функциями. Это допущение’ основано на вероятностном характере реакций синтеза полимеров, при котором макромолекулы могут характеризоваться любыми значениями молекулярных масс, но только в определенном интервале этих значений. Поэтому для полимеров (но не для олигомеров) этой дискретностью пренебрегают и считают распределение непрерывным от 0 до оо (хотя молекул с нулевой и — бесконечно большой молекулярными массами не существует). Характер кривых ММР в значительной степени зависит от механизма реакций синтеза полимеров, что дает возможность по форме экспериментальных кривых ММР детально анализировать эти механизмы.
Как известно, соотношение между возможными значениями случайной величины (например, молекулярной массы полимера М) и соответствующими им вероятностями называется законом распределения случайной величины, по которому ее значения являются аргументом, а вероятности — функцией. Интегральная функция распределения Q(M) определяет вероятность того, что случайная величина примет значения, не превышающие определенной величины, а дифференциальная q(M)—является плотностью распределения вероятностей. Обе эти функции находятся в следующем соотношении:
М
DQ (М) Г
9 (М) => ; Q(M)=> J q(M) dM. (1.4)
О
Дифференциальная и интегральная функции могут выражать как числовое [qn (М) и Q„(M)], так и массовое [qw(M) и Qu, (М) ] молекулярно-массо — вые распределения.
Если dn является относительным числом или долей (тогда j dn=1) макромолекул с молекулярными массами, лежащими в узком диапазоне от М до (M+dM), то непрерывная дифференциальная числовая функция ММР Судет равна:
Qn (М) =dn/dM~dNм/ (N0dM), (1.5)
Где NK — число макромолекул с молекулярной массой М; No — общее число макромолекул в образце полимера.
Принимая во внимание, что массовая доля фракции макромолекул, приходящаяся на тот же интервал dM, равна отношению’ массы этой фракции к общей массе образца полимера, непрерывную дифференциальную массо-
Еую функцию ММР можно записать:
Дл.(М) =Мдп(М)/Мп~ (МйЫм)/(ЫоМг. с1М) =с! тм/(т^М). (1.6)
В этом уравнении т и и то — массы соответственно макромолекул с молекулярной массой М и образца полимера.
Интегральные функции С„(Л1) и (ЛТ) вычисляют, интегрируя дифференциальные функции. При качественном сравнении ММР разных полимеров интегральные функции мало показательны. Функцию ММР полимеров можно, как и другие функции распределения, характеризовать набором моментов распределения }(М), которые определяются набором интегралов вида
Со
{М)йМ, (1.7)
Где V* — начальный момент порядка к (/<■=0, 1, 2, 3, …)•
Как известно, нулевой начальный момент характеризует площадь, огра
Ниченную кривой распределения и осью абсцисс, и может быть рассчитан по уравнению
СО
У0 = |/(М) *Ш—I. (1.8)
О
Моменты дифференциальной числовой функции распределения Цп(М) могут быть вычислены по уравнению
ОО
У*=. ^МкЯп(М) йМ. (1.9)
0
Отношение любого момента этой функции к ее предыдущему моменту является средней молекулярной массой полимера. Тогда
М,=У1/у0=Мп; М2=ч2/хх=Ми!.
Количественные значения этих моментов можно найти экспериментально, определяя молекулярные массы различными методами.
При использовании дифференциальной массовой функции распределения Чти(М) для набора моментов
ОО
^Мкцт(М)йМ. (1.10)
О
Из уравнения (1.10) можно получить:
Построение кривых ММР производят по экспериментально найденному фракционному составу. Графическое построение кривых может быть различным.
1. Кривая интегрального молекулярно-массового распределения (ММР) показывает зависимость кумулятивной (накопленной) массовой доли от молекулярной массы (рис. 1.1). Кумулятивная доля, имеющая, например, молекулярную массу, равную Ми является массовой долей всех полимергомо- логов с молекулярной массой, меньшей или равной М1. Функция, выражающая эту зависимость, называется функцией интегрального распределения.
2. Кривые дифференциального молекулярно-массового (или числового) распределения, приведенные на рис. 1.2, условно совмещены, хотя практиче-
|
Рис. 1.1. Интегральная кривая ММР (тк — кумулятивная массовая доля) |
Рис. 1.2. Кривые дифференциального молекулярно-массового (молекулярночислового) распределения.
Кривые условно совмещены; т — массовая доля; Л1 — мольная доля
Ски они не совпадают. Зависимость между массовой долей и характеризуется функцией дифференциального массового распределения, а взаимосвязь мольной доли и М„ называется функцией числового распределения.
Графически величины Мп и Мт являются абсциссами центров тяжести площадей, ограниченных кривыми числового или массового распределения и осью абсцисс (рис. 1.3). Положение центра тяжести распределения массы определяется первым начальным моментом.
Расположение повторяющихся звеньев в макромолекуле может быть различным, но среди имеющегося многообразия можно выделить три основных типа: линейные, разветвленные и сетчатые макромолекулы.
Линейные полимеры имеют вид открытых цепей или линейной последовательности циклов.
Разветвленные полимеры могут содержать короткоцепные и длинноцепные разветвления. Макромолекулы с длинноцепными разветвлениями могут иметь статистическую конфигурацию, быть гребневидными или звездообразными. Длина и конфигурация разветвлений сильно влияют на свойства полимеров.
Структуру сетчатых полимеров можно рассматривать как структуру полимерной системы, в которой молекулы могут содержать большое число разветвлений и циклов различного размера.
Полимеры обладают рядом специфических свойств, обусловленных их большой молекулярной массой, цепным строением макромолекул и их гибкостью (способностью макромолекул изменять свою конформацию под влиянием теплового движения звеньев или внешних механических сил), а также интенсивным проявлением сил вторичного взаимодействия между макромолекулами. При переходе от линейных цепей к разветвленным по
лимерам и сетчатым структурам некоторые свойства изменяются. Так, например, сильносшитые полимеры не растворяются, неплавки и неспособны к высокоэластическим деформациям.
 29 августа, 2013
29 августа, 2013  admin
admin 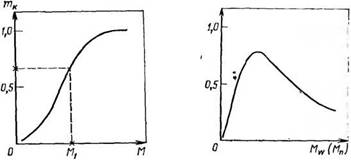
 Опубликовано в рубрике
Опубликовано в рубрике 