Б. В. Дерягин, 3. М. Зорин, Н. В. Чураев
(Институт физической химии АН СССР, Москва)
Явление смачивания, приводящее к формированию краевого угла между жидкостью и твердой подложкой, лежит в основе механизмов, определяющих равновесие и кинетику влаги в пористых телах. Величина равновесного краевого угла 0о определяется полем поверхностных сил и энергией взаимодействия жидкости с твердой подложкой. Слабое взаимодействие ведет к несмачиванию, сильное — приводит к растеканию жидкости по поверхности, ее полному смачиванию.
Развитие теории поверхностных сил [42] сделало возможным количественные оценки смачивания в зависимости от свойств твердой подложки и взаимодействующей с нею жид-
|
|
|
|
|
Рис. 13.1. Формирование равновесного крае Вого угла в0 при кон — 2Н Такте жидкости с поверхностями плоской Щели Пояснения см. в тексте |
‘А* .А—"
Кости. Впервые этот путь был намечен в работах А. Н. Фрум — кнна [552] и Б. В. Дерягина [553], положивших начало развитию теории смачивания. Взаимодействие жидкости с твердой подложкой, описываемое на основе изотерм расклинивающего давления смачивающих пленок П(/г), позволяет рассчитать значения 0о-
Применение теории Фрумкина — Дерягина долгое время сдерживалось недостаточной изученностью изотерм П(/і). В настоящее время достигнут значительный прогресс как в экспериментальном изучении изотерм расклинивающего давления смачивающих пленок [45], так и в развитии методов теоретического расчета различных составляющих расклинивающего давления, действующих в этих пленках [42].
Рассмотрение теории смачивания начнем с определения понятия краевого угла 0о. В состоянии равновесия краевой угол определяется в точке пересечения с подложкой продолжения невозмущенного поверхностными силами профиля капли или мениска (рис. 13.1, кривая 1).
|
(13.1) |
Мениск смачивающей жидкости контактирует при этом со смачивающей пленкой, равновесная толщина которой йо определяется уравнением изотермы П(/і). Значение h0 отвечает расклинивающему давлению, равному капиллярному давлению равновесного мениска: По = Ра. Между объемной частью мениска с постоянной (в пренебрежении силой тяжести) кривизной поверхности Ko = Pk/a (где ст — поверхностное натяжение) и плоской смачивающей пленкой образуется переходная зона 2 (см. рис. 13.1), где действуют одновременно капиллярные силы, вызванные кривизной поверхности слоя жидкости, и поверхностные силы, связанные с дальнодействующим полем подложки. В состоянии равновесия из условия постоянства давления во всех частях системы получим:
AK(h) +П(/і) =P*=const,
Где K(h) —локальная кривизна поверхности переходной зоны.
Это уравнение справедливо для пологих профилей переходной зоны (dh/dx<^. 1), когда для каждого ее элементарного участка dx применима изотерма U{h) плоского слоя.
Протяженность переходной зоны определяется радиусом действия поверхностных сил, обычно порядка Ю-6—10_о см. За пределами зоны влияния поверхностных силП(/і)=0, и тогда из уравнения (13.1) получаем уравнение Лапласа для невозмущенного мениска:
ВКа=Рь.
При h—»-/z0 слой жидкости становится все более пологим (К—>-0), и для плоского участка пленки из (13.1) получим:
По(Ло )=Р*.
Для плоской щели шириною 2Н и при полном смачивании для изотермы вида П—A/hn оценка протяженности I переходной зоны в направлении оси х получена в работе [554]: 1~ (Я/г0)1/2. Так, для щелей шириною 10 мкм и при ho~ Ю-5 см i«10~4 см.
Изложенный способ определения краевого угла неприменим в двух случаях. Значения 0о нельзя определить в узких щелях, где поля поверхностных сил перекрываются и область постоянной кривизны мениска отсутствует. Расчеты равновесия капиллярной жидкости и пленок требуют здесь применения другого подхода [555]. В особом рассмотрении нуждаются и такие случаи полного смачивания, когда продолжение мениска не пересекает подложку (рис. 13.1, кривая 3) и краевой угол не образуется.
С этими оговорками теория Фрумкина — Дерягина включает рассмотрение случаев как неполного (0о>0), так и полного смачивания. Ниже приводится один из выводов соответствующих уравнений теории, основанный на применении уравнения (13.1). Для мениска в плоской симметричной щели шириною H^>h кривизна цилиндрической поверхности мениска равна
Где h‘ и h" — первая и вторая производные толщины слоя жидкости по координате х.
Подставляя это значение K(h) в уравнение (13.1) и используя граничные условия: h‘ = 0 при h=h0 и h‘=—оо при /г = Я, получим следующее решение дифференциального уравнения (13.1):
ОО
ЯР* = а-ЫУг0+| П (h)dh. (13.2)
Ft
В том случае, когда краевой угол образуется (Эо^0), значение Pk можно выразить через cos Э0. В случае плоской щели, который здесь рассматривается,
Рь = а/г=а Cos 0О/Я
{г — радиус кривизны невозмущенной части мениска). Тогда вместо (13.2) получим:
A cos 0О= а+ПоЛо+Л. (13-3)
Где через Д обозначена величина интеграла. Сравним это выражение с известным уравнением Юнга:
A cos 0О = asv— osl- (13.4)
Для определения краевого угла 0О по этому уравнению надо знать разность удельных межфазных энергий твердой подложки на границе с газовой фазой osv и с жидкостью Osl. Так как не существует независимых от (13.4) методов определения ни каждой из межфазных энергий, ни их разности, уравнение Юнга, в отличие от уравнения (13.3), не позволяет определить величину краевого угла. Его используют обычно для нахождения разности osv—Osl на основании измеренных значений Эо-
Теория Фрумкина — Дерягина позволяет определить величину osv для твердой поверхности, покрытой смачивающей пленкой. Ее значение равно сумме межфазных энергий двух поверхностей жидкой пленки: одной, граничащей с газом (о), и второй, граничащей с твердой подложкой (osl). К этой сумме следует добавить изменение свободной энергии пленки (ПоЛо+Д) при ее утончении от оо до конечной толщины H0. В результате разность между OSv = O + OSl + IIo/Zo + А и Osl оказывается равной просто сумме о + lVto + A, которую и содержит уравнение (13.3).
Уравнение (13.3) дает возможность теоретически определять значения Эо по известной изотерме П(Л) смачивающих пленок данной жидкости на данной подложке. Экспериментальные и теоретические методы нахождения изотерм Щ/z) приводятся в [45].
Аналогичный вид имеет уравнение (13.3) и для цилиндрических капель на плоской подложке [556]. Это не удивительно, поскольку при H^>h0 (Я, в данном случае, — высота капли) условия равновесия не должны зависеть от знака кривизны поверхности за пределами области влияния поверхностных сил. Отличие состоит лишь в том, что значения По при этом отрицательны, так как капиллярное давление капли, имеющей выпуклую поверхность, имеет другой знак: По = Pk = — о/г, где г — радиус кривизны невозмущенной части капли. Уравнение (13.3) применимо и при Pk= 0, когда поверхность объемной жидкости плоская и слой имеет форму клина. В этом случае исчезает второй член в правой части уравнения, так как По=/5^ = 0.
Для капель со сферической поверхностью расчеты осложняются необходимостью учета второй кривизны поверхности капли. Для малых краевых углов 0о (когда можно принять Dh/dx<^) уравнение (13.1) записывается в следующем виде [557]:
Ofh"+ (ft’/p) ]+П(Л) =Pk=— 2a/V=const, (13.5)
Где h‘=dhldp, h‘^d^h/dp2; r=const— радиус кривизны поверхности капли; р — радиальная координата в плоскости подложки.
В общем случае решение этого нелинейного дифференциального уравнения может быть получено только численными методами. Его удается линеаризовать, используя упрощенную форму записи изотермы расклинивающего давления: „ I 0 при H > T;
11(h) к ^ (13.6)
‘ A(T0 — H) при 0 < H < T, V
Где a, t — параметры изотермы, характеризующие наклон ее устойчивого участка дП/д/г<0 и радиус действия поверхностных сил, соответственно.
В результате решения для равновесного краевого угла получается следующее выражение:
Tg^, =*(/-/„ +A.) jAjL, (13,7)
Где to — толщина пленки при П=0.
Как видно из этого выражения, при постоянстве параметров изотермы краевой угол капли 0о уменьшается при уменьшении ее размеров, сопровождающемся ростом отрицательного капиллярного давления. Такой эффект был, в частности, обнаружен экспериментально в работе [558] для капель воды диаметром менее 3 мм.
С ростом радиуса действия поверхностных сил T или уменьшением to при прочих равных условиях увеличиваются равновесные значения краевого угла, что связано с увеличением площади изотермы (13.6) в области отрицательных значений расклинивающего давления.
Область применимости уравнения (13.3) ограничена значениями 0о>О, когда П0/і0+А<0 и cos0o^l. В том случае, когда продолжение мениска в плоской щели не пересекает подложку, уравнение (13.2) позволяет определить капиллярное давление мениска Рк. Учитывая, что в состоянии равновесия Ph = По, из (13.2) получим:
Н-К(Рк) • 03.8)
Это уравнение связывает капиллярное давление мениска и радиус его кривизны r = a/Pk с полушириной щели Я и изотермой расклинивающего давления. Оно позволяет, взамен краевого угла, определить другой параметр, который можно использовать для характеристики условий полного смачивания,
|
|
|
Рис. 13.2. К определению единой характеристики смачивания 7= =А»/Ло |
Л*
|
Т-о |
|
Г<0 |
Г>0
Л именно разность h* = H—Г (рис. 13.2). Чем больше Л*, тем меньше радиус кривизны мениска и тем лучше смачивает жидкость поверхности щели. Преобразуя уравнение (13.8), найдем выражение для /г»:
А.=А0+(Д/Р*). (13.9)
При А = 0 h* — h0. При росте положительных значений А значения /г* растут, превосходя толщину равновесной пленки /г0.
В качестве единой характеристики смачивания, пригодной как при полном, так и при неполном смачивании, может быть использовано отношение 7 = /i*//io (см. рис. 13.2):
V = l + (13.10)
Значение 7 = 0, отвечающее 0о=О, отделяет область полного смачивания (^>0) от’области неполного смачивания (^<0). Чем выше положительные значения у, тем лучше смачивание. Так, в частности, для изотерм типа П=A/hn, проведя интегрирование и имея в виду, что Pk = Ro=A/h0n, вместо (13.10) получим:
7 = ^; A.-V7T7. (13-11)
При п = 3, что отвечает пленкам, устойчивым за счет действующих в них сил молекулярного отталкивания, 7=1,5 и /г* = = 1,5 Ло — При п—2, что отвечает пленкам, устойчивым за счет сил электростатического отталкивания, 7=2 и h* = 2h0. В общем случае изотерма П (Л) может складываться из многих составляющих расклинивающего давления и соотношение между Л* и h0 оказывается функцией Рь и изотермы П(/і).
При неполном смачивании (Эо^О) можно установить простую функциональную связь между параметром 7 и величиною равновесного краевого угла, образуемого мениском в плоской щели:
Т=—{г/ho) (1 — cos Go). (13.12)
При росте краевого угла 0о растут отрицательные значения 7, стремящиеся к бесконечности при 0о—>-90°, поскольку
Рис. 13.3. Изотермы расклинивающего давления П(Л) пленок воды на твердой поверхности
При этом г->-оо. Таким образом, изменение условий смачивания (от 0о = 9О° до полного смачивания) можно охарактеризовать с помощью одного параметра зависящего, как. видно из (13.6), от вида изотермы расклинивающего давления смачивающих пленок и ширины щели Я.
Для капель на твердой
Подложке могут реализоваться только условия неполного смачивания. Параметр ^ здесь неприменим, и единственной характеристикой смачивания является величина краевого угла. Для капель со сферической поверхностью малого радиуса на величину равновесного краевого угла влияет, кроме того, линейное натяжение периметра смачивания (см. ниже).
|
H, HM
+П 2-Ю2 О -2-Ю2 ~П, Па |
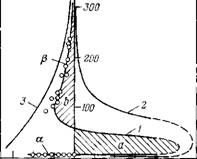
Рассмотрим теперь, от каких физических причин зависит смачивание или несмачивание поверхности. Для этого следует обратиться к анализу изотерм расклинивающего давления смачивающих пленок воды, показанных на рис. 13.3. Кривыми 1-—3 здесь изображены зависимости толщины h водных пленок от расклинивающего давления, или, что то же, от капиллярного давления равновесного с пленкой мениска. Кривая 1 относится к пленкам воды на поверхности кварца. Точками показаны экспериментальные данные, сплошная кривая представляет собой рассчитанную теоретически изотерму, учитывающую действие в пленке трех составляющих расклинивающего давления: молекулярной Пот, электростатической Пе и структурной Ш [47]. Ветви изотермы, где дП/5/і<0, отвечают устойчивым состояниям пленки. Пленки воды на кварце в области h между 60 и 10 нм (кривая 1) неустойчивы и не реализуются. При постепенном утончении водных пленок вначале возникает метаста — бильное состояние толстых (/t>100 нм) р-пленок. Время их перехода в термодинамически устойчивое состояние тонких а-пленок зависит от близости капиллярного давления к критическому Р* и от площади р-пленок. Чем площадь больше, тем выше вероятность образования в ^-пленке зародыша а-фазы. Существование толстых р-пленок воды обусловлено силами электростатического отталкивания заряженных поверхностей пленки (Пе>0). Так как в этом случае По/іо + Д>0, р-пленки полностью смачиваются водой. Ниже для этого случая будут сопоставлены экспериментальные значения h* с теоретическими, рассчитанными по уравнению (13.9).
Когда мениск объемной воды контактирует с ct-пленками, значения интеграла в (13.3) могут быть отрицательны в связи с частичным заходом изотермы П(А) в область П<0. Смена знака расклинивающего давления (кривая 1) связана с различными значениями потенциалов трі и — фг поверхностей пленки. Для расчета изотермы ПE(h) в этой области значений h использованы табулированные решения теории электростатических сил при условии постоянства потенциалов. При h<60 нм электростатические силы (при г|)і=7^і|з2) становятся силами притяжения (Пе<0). При дальнейшем уменьшении толщины пленок снова появляются силы отталкивания, но они связаны уже с действием молекулярных (Пт>0) и структурных (Ш>0) сил. Расчеты по уравнению (13.3) с использованием изотермы 1 (см. рис. 13.3) приводят к значению краевого угла воды на кварце е0«5°, близкому к экспериментальному, что служит подтверждением теории.
При подавлении сил электростатического отталкивания или при различном знаке потенциалов поверхностей пленки р-уча — сток изотермы не реализуется. При этом изотерма смещается в область ГКО (кривая 2 на рис. 13.3), что приводит, в соответствии с уравнением (13.3), к ухудшению смачивания.
Напротив, повышение по величине или сближение одинаковых по знаку потенциалов поверхностей пленки (т|зі и г|зг) приводит к росту сил электростатического отталкивания. В результате вся изотерма может оказаться в области П>0, что приводит к полному смачиванию (кривая 3 на рис. 13.3).
Таким образом, можно сформулировать условия, ведущие к изменению смачивания водой твердых поверхностей. Влиять на вид изотерм Yl(h) смачивающих пленок воды можно в основном за счет двух эффектов — зарядовых (Пе) и структурных (IL). Молекулярные силы, зависящие от спектральных характеристик воды и твердой подложки, мало чувствительны к составу водного раствора, температуре и заряду поверхностей. Поэтому для данной твердой подложки значения Пт практически постоянны. Влиять на структурные силы можно посредством трех факторов: повышением концентрации электролита и температуры, что ведет к уменьшению структурного отталкивания, а также путем адсорбции молекул ПАВ, что изменяет характер взаимодействия молекул воды с твердой поверхностью. Ухудшение смачивания, необходимое для повышения эффективности флотации, достигается обычно путем адсорбции ионогенных ПАВ. При этом важно, чтобы ПАВ избирательно адсорбировалось на одной из поверхностей пленки, придавая ей заряд, обратный по знаку заряду другой поверхности. В этом случае возникают силы электростатического притяжения (Пе<0), что сдвигает изотерму в область ГКО. Адсорбция ПАВ может приводить одновременно и к гидрофобизации твердой подложки, что может уменьшить структурное отталкивание или, в случае высокой степени гидрофобизацин, к смене знака также и структурных сил (П«<0). При этом могут быть достигнуты еще более высокие значения краевого угла [47].
Напротив, все меры, ведущие к росту сил электростатического и структурного отталкивания, улучшают смачивание. Эта цель достигается приданием высокого и одинакового по знаку потенциала поверхностям пленки и (или) гидрофилизацией подложки, например путем увеличения числа центров, способных к образованию водородных связей с молекулами воды. При адсорбции неионогенных гидрофильных ПАВ или полимеров может проявиться дополнительно действие сил стерического отталкивания адсорбционных слоев. Понимание причин, управляющих смачиванием, позволяет в каждом конкретном случае выбирать оптимальные методы для решения практических задач.
Область применимости уравнения (13.2) ограничена такими значениями толщины смачивающих пленок, когда их еще можно считать частью утончившейся жидкой фазы. При плохом смачивании (Эо^90°) на твердой поверхности образуется двухмерная адсорбционная фаза: толщина пленок не превышает монослоя. Здесь применимо другое выражение, вытекающее из уравнения Гиббса, связывающего величину адсорбции молекул (Г) с изменением межфазного натяжения (ctsv) в зависимости от давления пара адсорбата р [45]:
"s
Acos Є0=а+ J Г(р)сИпр, (13.13)
P
Где ps — давление насыщенного пара.
Уравнение (13.13) переходит в (13.2) при замене Г отношением Ho/Vm, где Vm — молярный объем жидкости, и при использовании известного термодинамического соотношения между р и П:
VmTl=RT In (ps/p), (13.14)
Где R—-газовая постоянная, Т — температура.
Основная трудность расчета значений краевого угла 0О по уравнениям (13.2) и (13.3) состоит в том, что при 0о>О изотермы расклинивающего давления 11(H) или изотерма адсорбции Г (P/Ps) частично располагаются в области пересыщения (П<0, P/Ps> П. Значения cos6o пропорциональны при этом разности площадей а и Ъ графика изотермы (см. рис. 13.3). Так как экспериментально находить изотермы в области пересыщения трудно, эти участки изотерм можно найти только расчетным путем на основании теории поверхностных сил. Такая расчет-
2 4 Б 8 Я? рН л 1 г 1 1—
TOC o "1-3" h z V
To -3 ■—1 / —- Д /
Л ч /
^ ил/ °
А X
/
5
0 U———- 1——— 1———- l__J
10~5 10~3 10 1 С, моль/л
Рис. 13.4. Результаты расчетов краевых углов 0о для водных растворов КС1 различной концентрации (/) и +П 2-Ю4 0 -2-Ю4 -п. па
При различных значениях рН (2)
Рис. 13.5. Изотермы П(А), рассчитанные для Ю-3 М водного раствора КС1
С добавками ПАВ: 100 MB = const; ф2=—100 мВ (/): —75 (2); —65 (3); —45 (4); —35 (5); —25 (6):
+ 100 мВ (7)
Ная программа была реализована в работах [47, 559] применительно к водным растворам и несколько ранее — применительно к более простому случаю неполярных жидкостей, когда можно ограничиться учетом одних только молекулярных сил [560].
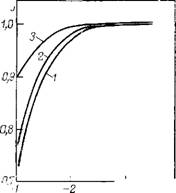
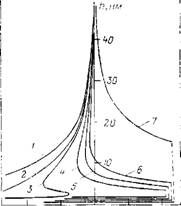
На рис. 13.4 показаны результаты расчетов по уравнению (13.3) краевых углов 0О для водных растворов К. С1 различной концентрации (кривая 1) и разных рН (кривая 2) при сохранении в последнем случае постоянной ионной силы раствора / = 10-2 моль/л [559]. При проведении расчетов Пe(h) использованы известные концентрационные зависимости потенциалов поверхности кварц — раствор (т|зі) и поверхности водный раствор— воздух (af2). Для изотермы Пт=Л/(6я/і3) приняты значения постоянной Л = 7,2-10~20 Дж. Для изотермы структурных сил принята экспоненциальная зависимость [47], параметры которой использовали в качестве подгоночных при согласовании теоретических расчетов 6о с экспериментальными данными для растворов К. С1 различной концентрации [561]. Рост значений 00 с повышением концентрации электролита (кривая 1) объясняется, как можно показать на основании проведенных расчетов, двумя причинами: уменьшением толщины граничных слоев воды с особой структурой, что ведет к ослаблению сил структурного отталкивания, и снижением потенциалов — фх и т|)2, что уменьшает также и силы электростатического отталкивания.
|
|
Улучшение смачивания при росте рН (кривая 2) вызвано В основном ростом потенциалов — фі и г|32 поверхностей пленки
в результате адсорбции потенциалопределяющих ОН_-ионов. Заметим, что при ионной силе Ю-2 моль/л (кривая 2) зависимости краевых углов описываются уравнением (13.3) с изотермой П(Л), включающей только две составляющие расклинивающего давления — электростатическую и молекулярную. Структурные силы при такой концентрации электролита малы (Ш«0), и их можно было не принимать во внимание.
С разрушением особой структуры граничных слоев связан также и известный эффект ухудшения смачивания при повышении температуры [562]. На рис. 13.5 приводятся результаты расчетов изотерм расклинивающего давления смачивающих пленок водного Ю-3 М раствора КС1 с добавками ионогенных ПАВ. Для молекулярных сил принята та же константа А; для структурных сил — экспонента Ш = С5ехр(—H/X), где Cs = = 104 Н/см2 и //=0,25 нм. Исходной, без добавок ПАВ, является изотерма, показанная кривой 6. Потенциалы поверхностей кварца (if>i) и пленки (т|з2) принимали в этом случае равными —100 мВ и —25 мВ, соответственно. Расчеты по уравнению (13.3) приводят к значению 0о = 8° (см. рис. 13.4). Влияние добавок ПАВ сводилось в проведенных расчетах к изменению потенциала — фг вследствие адсорбции ПАВ на поверхности пленка—газ. Адсорбция анионоактивного ПАВ, повышающая отрицательный потенциал т|з2, приводила к улучшению смачивания. Так, при г|)2= —35 мВ рассчитанный краевой угол уменьшается до 7°, а при г|)2 = —45 мВ — до 5°. Дальнейший рост г|з2 (кривые 1—3) обеспечивает уже полное смачивание поверхности кварца. Если же на поверхности пленки адсорбируется ка — тионоактивный ПАВ, заряжающий поверхность пленка^-газ положительно (if>2=+100 мВ), в то время как поверхность подложки остается заряженной отрицательно, краевой угол растет до 28° в связи с тем, что электростатические силы вызывают притяжение поверхностей пленки (Пе<0). Полученные результаты находятся в хорошем согласии с результатами прямых измерений краевых углов растворов КС1 с добавками анионоактивного натрийдодецилсульфата и катионоактивного цетилтриметиламмонийбромида [563].
Формирование равновесных краевых углов требует в ряде случаев значительного времени в связи с замедленным массо — обменом между объемной жидкостью и тонкими смачивающими пленками. Кинетика перехода к состоянию равновесия контролируется при этом вязким сопротивлением пленок и диффузией компонентов водного раствора, равновесная концентрация которых в объемной фазе и тонкой пленке может быть различной. Вследствие этого вначале может быстро устанавливаться механическое равновесие в объеме капли или мениска при отсутствии механического и термодинамического равновесия с жидкостью в пленке. Возможность реализации ряда состоя-
ний механического равновесия приводит к явлению статического гистерезиса краевого угла. При этом, как было показано — в работе [556], существенную роль играет переходная зона между мениском и пленкой. Состояние ее механического равновесия, определяемого выполнением условия (13.1), нарушается при двух значениях капиллярного давления Ph и, соответственно, при двух значениях краевого угла — наступающего (0л>0о) и отступающего ((9д<60). В промежутке между 0л и 0Д возможно множество состояний механического равновесия, что затрудняет, а в ряде случаев делает практически невозможным определение среди них термодинамически равновесного краевого — угла. Чем лучше смачивание и чем толще смачивающая пленка, тем быстрее осуществляется переход к равновесию и тем меньше различие между 0л и 0Д.
Раньше считалось, что гистерезис краевого угла вызван; только неровностями поверхности или ее химической неоднородностью—наличием участков с разными равновесными краевыми углами. Рассмотрение механической устойчивости переходной зоны показало, что гистерезис возможен и на гладкой однородной поверхности. При этом значения Qa и 0Д могут быть также определены на основании изотерм расклинивающего давления П(Л)[556]. Для изотерм типа 1 на рис. 13.3 значения 0л лежат между 0о и 90°, а значения 0Д близки к 0, так как краевой угол образуется с метастабильной ^-пленкой, формирующейся за отступающим мениском. >
До сих пор рассматривались состояния термодинамического- или механического равновесия системы мениск — пленка. При движении капель или менисков распределение давлений в переходной зоне и пленке меняется, что приводит к изменению также и поверхности мениска. Если теперь продолжить невозмущенный профиль мениска до пересечения с подложкой, то определенное этим формальным методом значение краевого угла обнаруживает зависимость от скорости V смещения периметра, смачивания. Динамические краевые углы 0d начинают отличаться от статических 0о и превышать их при у>10~3 см/с. Теория динамических краевых углов развита пока только для случая полного смачивания, когда мениск наступает с постоянной: скоростью на равновесную смачивающую пленку. Решение удается получить численными методами на основе уравнения (13.1) [564]. Полагая, что условие пологости профиля переходной зоны сохраняется и при течении, из (13.1) можно получить следующее выражение для градиента давления в направлении течения:
|
Dsh <ДІ (H) ds h dU dh
|
|
DP Dx |
|
= а |
(13.15)
Где для кривизны поверхности слоя использовано приближение K—d2h/dx2.
В уравнении (13.15) Р—Р0—Р{х)— Щх)—так называемое гидродинамическое давление в пленке, равное давлению в фазе газа Ро за вычетом локальных значений капиллярного и расклинивающего давления. Выражение (13.15) для градиента Р можно теперь подставить в известное уравнение гидродинамики тонких слоев при v = const:
|
Где г) — вязкость; h(x)—локальная толщина слоя жидкости и h0 — толщина равновесной пленки. |
|
(13.16) |
Стационарное решение получающегося дифференциального уравнения дает уравнение для профиля движущейся жидкости.
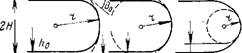
На рис. 13.6 показаны рассчитанные на ЭВМ профили мениска, движущегося с разной скоростью v в плоской щели [564]. Для определения Qd использовали участок профиля постоянной кривизны, непосредственно примыкающий к зоне течения и находящийся поэтому еще в области пологости слоя жидкости h(x). На рис. 13.7 приводятся некоторые из результатов расчетов зависимостей cos от величины критерия Дерягина De = yri/a, характеризующего безразмерную скорость смещения мениска. Расчеты сделаны для изотермы вида П(/і) = =A/hz (при А = Ю-21 Дж) и различной полуширины щели Я. Как видно из рис. 13.7, повышение скорости v приводит к росту значений 0d. Отличия 0<* от статического значения 0о = О начинают проявляться при De>10~3. Чем уже щель и чем, соответственно, меньше толщина равновесной смачивающей пленки Л0, тем меньше течение нарушает профиль мениска.
Экспериментальные исследования динамических краевых углов для воды на поверхности кварца показали, что значения 0d начинали превосходить равновесные значения 0о»1О° при v^ 10-3 см/с, достигая 75—80° при у>0,1 см/с [565]. Эти данные качественно согласуются с теоретическими, но расходятся
|
Рис. 13.6. Профили мениска в плоском капилляре при полном смачивании: А — в покое; б, в — при движении с растущей скоростью |
Рис. 13.7. Рассчитанные для случая полного смачивания зависимости динамического краевого угла 9л от
Скорости движения мениска. 1: Н= ю-2 см, ft0= 15 нм; 2: Н= 1,25-10—3 см, Ло=7,4 им; 3: Н= 1,25-Ю-5 см, /10=1,6 им
Количественно. Теоретически отличия 0d от 00 должны были бы наблюдаться при более высоких V. Это расхождение связано с тем, что теория развита только для условий полного смачивания и монотонной изотермы П(Л) типа кривой 3 на рис. 13.3. Для воды на кварце характерен другой тип изотермы — s-образной (кривая 1 на рис. 13.3), что существенно меняет форму профиля переходной зоны и, следовательно, количественные результаты расчетов.
|
Cos а |
|
-з цыш2’3 |
Для другого крайнего случая — очень тонких адсорбционных пленок, когда процесс смещения мениска контролируется поверхностной диффузией молекул воды (поверхностной вязкостью г)5), Т. Блейк и Д. Хайнес [566] получили решение для 0d на основе теории Эйринга абсолютных скоростей реакции:
|
(13.17) |
|
V =—— sh |
(cos 60 — COS 6rf)
AnkT
Где с — некоторая константа; АП — поверхностная концентрация адсорбционных центров; k — постоянная Больцмана.
Используя это уравнение, Е. В. Грибанова и Л. И. Молчанова [567] получили из измерений для воды в стеклянных капиллярах и кварцевых щелях значение Дя=1,4-1014 см-2, близкое к концентрации ОН-групп на поверхности стекла. Заметные отклонения значений 0d от 0О начинались также при V> >10"3 см/с.
Существование переходной зоны между мениском и пленкой приводит к еще одному эффекту, в общем случае предсказанному В. Гиббсом, — эффекту линейного натяжения [568]. По — аналогии с поверхностным натяжением, когда переходная зона между жидкостью и паром заменяется плоскостью натяжения, : переходная зона между мениском и пленкой может быть заменена линией трехфазного контакта, которой приписывается некоторое линейное натяжение х. В отличие от а значения к могут быть как положительными, так и отрицательными, что вызывает стремление кругового периметра смачивания к стягиванию— в первом случае или к расширению—во втором.
При замене переходной зоны линией трехфазного контакта в уравнение Юнга вводится дополнительный член к/г:
OcosQ0=osv — osL±(x/r) (13.18)
(г —радиус периметра смачивания). Ясно, что действие линейного натяжения должно проявляться тем заметнее, чем меньше радиус кривизны г. При г—>-оо (для прямолинейной границы смачивания) член с линейным натяжением не влияет на величину равновесного краевого угла. В случае капель на плоской подложке положительные значения х ведут к росту 0О, а отрицательные—к их уменьшению. Для плоских пленок, окруженных вогнутым мениском, влияние знака х обратное, с чем и связано введение двойного знака перед последним членом в уравнении (13.18).
Оценки линейного натяжения дают для воды и водных растворов значения х, по порядку величину равные Ю-10— 10-11Н [568]. Таким образом, вклад третьего члена в правой части уравнения (13.18) становится ощутимым при /•< Ю-4— Ю-5 см, т. е. для капель и пленок очень малого радиуса. Весьма заметным проявление линейного натяжения может быть, в частности, при флотации — на начальной стадии сближения пузырьков газа с частицами, а также при конденсации воды на твердых поверхностях — на стадии образования зародышей конденсата.
Теория линейного натяжения для капель на плоской твердой подложке была развита в работе [557]. Расчеты х выполняли на основе уравнения (13.18) по разности между значениями a cos 0О, найденными по уравнению (13.5) профиля переходной зоны, и в предположении, что переходная зона отсутствует и невозмущенный мениск прямо соприкасается с плоской пленкой. Так как линейное натяжение обусловлено существованием переходной зоны, ясно, что разность вычисляемых значений •ccos 0о как раз и связана с членом к/г.
Как было показано в работах [557, 569], линейное натяжение зависит от радиуса кривизны г, что объясняется зависимостью формы профиля переходной зоны от г. Однако если влияние кривизны на поверхностное натяжение проявляется при радиусе кривизны поверхности порядка межмолекулярных расстояний, то в случае линейного натяжения влияние кривизны периметра смачивания проявляется при много больших г — порядка радиуса действия поверхностных сил.
Аналитическое выражение для х было получено для упрощенной изотермы расклинивающего давления (13.6), аналогичной по виду изотерме 1 на рис. 13.3. Соответствующее выражение для х имеет следующий вид [557, 569]:
________________________________________ 2g/’tg9°—————- (13.19)
1 + (2/г) (o/ayl*
Где а и T — параметры модельной изотермы П(/г).
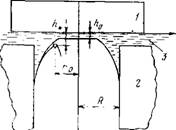
Рис. 13.8. Формирование смачивающей пленки толщиною Hn и радиусом г0 на твердой подложке I в отверстии трубки 2 Радиуса R при отсасывании жидкости через щель 3 под действием капиллярного давления
При г—>- оо значения х->-хо = = —2a/tg0o. Для небольших 0О, когда образуется плавный профиль переходной зоны, значения хо отрицательны и составляют по порядку величины Ю-11 Н, что согласуется с экспериментальными данными для пенных пленок [570].
Недавно впервые удалось экспериментально исследовать профиль переходной зоны между мениском и пленкой на твердой подложке и проверить правильность уравнений (13.8) и (13.9) теории полного смачивания [571].
Смачивающие пленки формировали на полированной кварцевой пластинке 1 (рис. 13.8) путем приближения к ней мениска жидкости в трубке 2 радиусом R=0,5-^-1 мм. Жидкость отсасывали из трубки через щели 3. Толщину пленки ho в состоянии равновесия с окружающим ее мениском измеряли по интенсивности отраженного света. Радиус пленки л> составляет, в зависимости от капиллярного давления мениска Pk, несколько десятков мкм. Одновременно с измерением толщины фотографировали интерференционные кольца от мениска, что позволяло определить его профиль H(R), где г — радиальная координата.
Анализ полученных экспериментально профилей H(R) для воды и водных растворов КС1 низкой концентрации показал, что продолжение профилей, рассчитываемое по уравнению Лапласа для симметричного мениска
Г sin 0 = (г2 — г20), (13.20)
Не пересекает подложку, т. е. имеет место полное смачивание. Здесь 0(г)—текущее значение угла, для которого tg0 =Dh/Dr (см. рис. 13.8).
Решение уравнения (13.20) позволяет найти координату г0, при которой теоретический профиль мениска проходит через минимум, чье положение отвечает толщине слоя /і*. Как было показано выше, величина f = /i*//i0 является характеристикой смачивания. Результаты некоторых измерений А* и H0 для водных растворов КС1 при Рй=1,5-10~2 Н/см2 представлены ниже:
10-4 моль/л 10-® моль/л
H" НМ 145 1 V — 1 41 71 Vt= 1 2
|
|
Ho, им 102,5 ) 1,41 59 J V=
Протяженность переходной зоны в тангенциальном направлении I можно оценить по разности г0—гр, где гр — радиус той (плоской) части смачивающей пленки, интенсивность отражения света от которой постоянна. Для концентрации КС1, равной Ю-4 моль/л, /да 6 мкм. Повышение концентрации приводит к уменьшению протяженности переходной зоны.
|
|
Полученные экспериментально значения f можно сопоставить с теорией. Большие значения равновесной толщины пленок и полное смачивание показывают, что здесь действуют преимущественно силы электростатического отталкивания. Задаваясь потенциалами поверхности кварца (|зі) и поверхности пленки (■фг)» можно по таблицам Деверо и де Бройна рассчитать изотерму электростатических сил Пe(h). Для Ю-4 М раствора КС1 на основании работ [14, 572] можно принять — фі = —150 мВ и |)2 = —45 мВ, а для 10_3 М раствора if>i =—125 мВ и if>2 = = —45 мВ. Рассчитанные изотермы Пе(/і) при условии if> = const спрямляются в логарифмических координатах с коэффициентом корреляции 0,996, что позволяет аппроксимировать изотерму степенной функцией Tl=A/hn. Для 10_4Л1 КС1 показатель степени я = 2,87, для 10-3 М п=6. Подставляя эти значения п в уравнение (13.11), получим теоретические значения параметра у, равные 1,5 для Ю-4 М и 1,2 для Ю-3 М растворов. Эти значения удовлетворительно согласуются с приведенными выше (см.
Рис. 13.9. Интерференционная картина от смачивающей пленки, переходной зоны и мениска на поверхности кварца.
Водный раствор NaCl (10—4 М)
Рис. 13.10. Профили переходной зоны между мениском и пленкой: Радиус пленки г0 = 15 мкм; 10-‘ М водный раствор NaCl; / — эксперимент; 2 — профиль невозмущенного мениска; 3 — расчет
С. 225), что служит экспериментальным подтверждением теории. Аналогичные результаты были получены ранее для воды и ряда водных растворов [571].
При низкой концентрации электролита протяженность переходной зоны составляет 5—6 мкм, что дает возможность ее изучения оптическими методами. На рис. 13.9 приведена одна из фотографий интерференционной картины от пленки и мениска. В нижней части рисунка изображена записанная с помощью фотометра фотограмма негативного изображения этой картины. При малом радиусе пленки г0, соизмеримом с I, плоский центральный участок отсутствует. То, что можно назвать в данном случае пленкой, представляет собою перекрывающиеся переходные зоны.
По фотограмме был рассчитан профиль мениска и переходной зоны (кривая 1 на рис. 13.10). Кривая 2 дает профиль невозмущенного поверхностными силами мениска, построенный по уравнению (13.20). Минимум на этой кривой определяет толщину слоя /і*. Затем можно было попытаться построить также и теоретический профиль переходной зоны. Однако теория развита пока только для мениска и переходной зоны в плоском капилляре, причем аналитическое решение получено для изотерм вида П=A/h" [554]. Соответствующее уравнение для профиля переходной зоны h(x) имеет вид:
Н н І н
Х = J (Pk — Ah-") Dh П (Рк — Ah~N) Dh H LUo I H -1/2
— U Dh, (13.21)
Где X — тангенциальная координата (см. рис. 13.1).
Ширину эквивалентной щели Я определяли так, чтобы капиллярное давление цилиндрического мениска в плоской щели и мениска в трубке (см. рис. 13.8) было одинаковым. Это обеспечивало равенство расклинивающего давления П0 = РА в пленке на поверхностях щели и поверхности подложки в условиях проведенных экспериментов. Рассчитанный с помощью уравнения (13.21) профиль переходной зоны (при п=2,87 и Л = = 9,54-10~12, если П выражено в дин/см2 и h — в см) показан на рис. 13.10 (кривая 3). Как видно, совпадение экспериментального и теоретического профилей достаточно хорошее.
Проведенный обзор состояния теории смачивания водой твердых поверхностей, достаточно гидрофильных для того, чтобы краевые углы не превышали бы 30—40°, показывает, что использование изотерм расклинивающего давления П(/і) открывает новые возможности теоретических оценок условий смачивания и управления смачиванием. Задачей дальнейших исследований является получение экспериментальных изотерм расклинивающего давления смачивающих пленок на различных подложках и для растворов различного состава. Это позволит уточнить значения параметров, входящих в уравнения изотерм, что сделает результаты расчетов более надежными.
 24 октября, 2012
24 октября, 2012  admin
admin 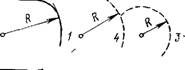


 Опубликовано в рубрике
Опубликовано в рубрике 