Структура и свойства объемной воды и воды вблизи границы раздела фаз, как вытекает из результатов многочисленных теоретических и экспериментальных исследований, существенно различаются [116, 586, 587]. В частности, вблизи границы раздела фаз проявляется заторможенность и анизотропия молекулярной подвижности, изменяются характеристики молекулярного и протонного обмена, формируются специфические ориен — тационные структуры [573—580].
В [575, 579] подчеркивается, что микродинамика граничной воды может быть тесно связана с микродинамикой границ раздела, вблизи которых она формируется. К. Пакер [575] предложил модель микродинамики граничной воды, в которой разделены быстрые (f) и медленные (s) движения, связанные с подвижностью индивидуальных молекул воды (/) и переориентацией микрообластей (время корреляции Тя) или конечным временем пребывания молекулы воды в пределах данной микрообласти [Tiat~d2/(4D)] (рис. 14.1). Вклад медленных движений в спектр молекулярных движений воды может возникать вследствие заторможенной подвижности воды вблизи активных центров поверхности, анизотропии ориентационного упорядочения или анизотропии коэффициента трансляционной диффузии (D^D±) вблизи межфазной границы.
Наиболее важной задачей ЯМР-спектроскопии воды в гетерогенных системах является установление однозначной взаимосвязи между экспериментальными данными, получаемыми с по-
|
Рис, 14.1. Общая схема микродинамики воды в гетерогенных системах |"575, 579] Микрообласти характеризуются размерами ha, h^, с! и т. д. и направлены под различными углами к внешнему магнитному полю (9а, 6^). F и В — области, соответствующие свободной и связанной воде; X —толщина ориентационио-упорядоченной области (В), So2 и — ориентациониые параметры порядка, Dll и D — компоненты тензора трансляционной диффузии в граничной области; xR — время корреляции, характеризующее броуновскую вращательную диффузию микрообласти в целом; т1а1 — время диффузии молекулы воды в латеральном направлении или время пребывания молекулы в пределах микрообласти; Xftr^F, тех н — времена вращательной и трансляционной диффузии и время протонного обмена для свободной воды; т’ех н, Tcro3s — времена протонного и кросс-релаксационного обмена с поверхностными (Группами; 1(r)Bf, — времена вращательной корреляции в области В, соответствующие вкладу быстрых (/) и медленных (s) движений в релаксационные процессы |
Мощью этого метода (временами релаксации или химическим сдвигом), и параметрами, характеризующими структуру и динамику граничной воды. Рассмотрим некоторые отличительные особенности ЯМР-спектроскопии воды в гетерогенных системах.
Природа неэкспоненциальной релаксации воды в гетерогенных системах. Спад намагниченности Af(if) воды в гетерогенных системах иногда описывается многоэкспоненциальной функцией вида
М (0 = М (0) = 2 Ра ехр { — TjT (л) ]},
П
Где рп — относительная доля вклада п; Т(п)—время релаксации [7] (л) илн Т2(п)] [573—5751-
Природа данной неэкспоненциальности может быть обусловлена несколькими различными причинами. Теория мультифаз — ной релаксации воды в гетерогенных системах с учетом химического обмена развита Д. Циммерманом и В. Бриттином [588]. Полезные соотношения для наблюдаемых времен релаксации и населенностей в двухфазной системе можно найти в [574, 589]. Многоэкспоненциальность может быть обусловлена конечным размером и формой микрообластей, в которых находится вода [590]. Характерные размеры микрообластей, для котОрых вАжен этот механизм, определяются соотношением /^/с~Уб£>Гі(2)Л: 10—100 мкм. Данный подход можно успешно использовать для интерпретации экспериментальных данных по протонной релаксации воды в гетерогенных системах.
В протонной ЯМР-спектроскопии многоэкспоненциальность может быть также связана с кросс-релаксацией или спиновой диффузией между протонами воды и протонами поверхности. Теория кросс-релаксации в гетерогенных системах построена в работе [591]. Анализ экспериментальных данных показывает, что этот механизм чрезвычайно важен для водных растворов полимеров и биологических объектов [576, 591]. Наиболее отчетливо важность этого механизма продемонстрирована с помощью методики двойного разонанса [592], а также путем селективного возбуждения сигналов ЯМР в узком спектральном диапазоне [593].
На ядрах 170 (/=5/г) намагниченность спадает как взвешенная сумма трех (/+1/г) экспонент, причем одноэкспоненциаль — ный спад наблюдается только при условии предельного сужения ft)oTc«Cl. Для граничной воды спад намагниченности является почти экспоненциальным, а ошибка, связанная с пренебрежением эффектом многоэкспоненциальности, не превышает нескольких процентов [594].
Распределение времен корреляции. По определению, процесс характеризуется одним временем корреляции тс, если автокорреляционная функция, соответствующая этому процессу, является экспоненциальной [595, 596]:
G(T) =ехр (— T/Тс). (14.4)
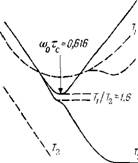
В спектроскопии ЯМР строго однокорреляционным, согласно этому определению, является только процесс броуновской вращательной диффузии. Зависимости времен релаксации Ті и Г2 от тс=тг~1/Г для данного процесса представлены на рис. 14.2 сплошными линиями. В минимуме Ті (при 6>оТг« 0,616, <oo = 2nvo — резонансная частота) выполняется условие Т/Т2~ «1,6. Экспериментально обычно получают зависимости Ті и Т2 От тс~1/7 которые схематически представлены на рис. 14.2 пунктирными линиями. Минимум Ті более пологий, чем для броуновской вращательной диффузии (иногда наблюдаются даже два минимума [597]), и в точке минимума Ті выполняется условие Ті/Гг^І. Это свидетельствует о наличии распределения времен корреляции, т. е. о том, что вид временной автокорреляционной функции заметно отличается от экспоненциальной [576]. В гетерогенных системах для воды возможно однородное и неоднородное распределение времен корреляции [596]. Однородным называется распределение, которое связано с внутренней неэкспоненциальностью функции G(T), что справедливо, на-
Рис. 14.2. Схематическое изображение зависимостей Ti(Xc) и Т2(хс) для гомогенных (сплошные линии) и гетерогенных (пунктирные линии) систем
Пример, для трансляционной диффузии, систем с анизотропной диффузией или пониженной размерностью. Неоднородное распределение связано с пространственной неоднородностью, например с неоднородностью энергий активации в различных точках гетерогенной системы. Используя для
Описания неоднородного распределения тс логарифмически-нормальный закон, Г. Резинг [573] из экспериментальных значений ТІ и Т2 вычислил функции распределения времен релаксации воды в цеолитах и некоторых других гетерогенных объектах. Однако ширина полученных распределений, по-видимому, является завышенной [591, 598], так как наблюдаемые зависимости Ті (тс) и ТІ(Хс) можно отчасти объяснить и эффектами кросс-релаксации, а также при учете явлений, связанных с однородным распіределением времен корреляции.
|
|
|
/ |
|
|
|
|
|
/ |
|
Тг ~t/T |
Анизотропия вращательной подвижности. Теоретические расчеты и данные машинного моделирования свидетельствуют о том, что молекулы воды вблизи межфазной границы ориента — ционно упорядоченны [2, 599, 600]. Наблюдаемый экспериментально поверхностный скачок потенциала и экспоненциальное отталкивание межфазных границ в тонких пленках также объясняется поляризацией молекул воды в поверхностной области [601, 602]. Вследствие ориентационной анизотропии возникает остаточное расщепление линий ЯМР воды и наблюдаются некоторые особенности ЯМР релаксации воды в гетерогенных системах.
|
(14.5) |
|
(14.6) |
Для обобщенной модели анизотропной подвижности получили следующее выражение для величины остаточного расщепления линий ЯМР воды [579]:
AVd(q) = AVd(<3) I (3cos20BJV— 1)S [,
Где для протонов
Но ЗЯу*
4л 4лг3нн
и для квадрупольных ядер (2Н, 170)
Avq=3X/[4/(2/-1)]. (14.7)
Здесь Qbn — угол между направлением внешнего магнитного поля Во и направлением нормали к границе раздела N; 5 — параметр остаточной анизотропии
S(‘H) =—0,5S20—0,615V,
S(2H) » 0,1S20—0,41S22; (14.8)
S(I70) « — 0,03S2o+0,80S22
(So2 и 5г2 — параметры ориентационного порядка, определенные в [579]). Для вычисления абсолютных значений So2 и S22 Необходимо использовать все три уравнения для S(‘H), 5(2Н) и S(170), так как экспериментально определяются только абсолютные значения параметров анизотропии. Практически значения 502 и 5г2 вычисляются с большой степенью неопределенности [604], так как величина S(‘H) может содержать большой вклад, связанный с протонным обменом, а вид приближенных уравнений для S(2H) и 5(170) зависит от геометрии молекулы воды вблизи гидрофильной поверхности и величины Т1 для нее.
Экспериментально определяемые значения отношений |S(x)/5(y) | для воды в различных гидрофильных системах обычно приблизительно инвариантны и слабо зависят от состава системы и температуры; |S(2H)/S(‘H) | да 1-М,7 и |5(170)/ /S(2Н) | да 1,8^-2,5 [579]. Это объясняется слабой чувствительностью этих величин к отношению S22/S02, которая проявляется только вблизи 522/S02«0 [604].
Для модели аксиального анизотропного вращения вокруг оси д вместо (14.5) получается другое выражение [603]:
AvD«3)=AvD(Q)P(eSA,)P2(0AAr)[2P2(eAF)+^ sin20AFсоз2фд/>], (14.9)
Где P2(0) = V2(3Cos20—1); 0Ajv — угол между осью вращения Д и N; (0Aj?> фдг} — сферические углы вектора Д в главной системе координат F Тензора взаимодействия. Ось zF этой системы совпадает с направлением ГннОН), г0н(2Н) и —ц("0), где р. — днпольный момент молекулы Н20 [579].
Модель аксиального анизотропного вращения использована для интерпретации экспериментальных данных по остаточному расщеплению линий ЯМР воды в гидратах слоистых силикатов [597] и упорядоченных образцах лиотропных жидких кристаллов [603].
Теория релаксации для систем с анизотропной подвижностью чрезвычайно сложна, и в общем виде она окончательно еще не разработана. Обзор современного состояния данной проблемы можно найти в работах [579, 603]. Подробно рассмотрен лишь случай макроскопически анизотропных систем, для которых остаточное расщепление снимается в результате быстрого диффузионного движения, а параметр остаточной анизо
тропии локально-упорядоченной жидкости мал. В [579] рассмотрена обобщенная двухступенчатая модель релаксации анизотропной жидкости, в которой разделен вклад быстрых и медленных движений (см. рис. 14.1). Автокорреляционная функция для данной модели может быть представлена в виде суммы двух вкладов:
0 « " (‘ — Т^тг) °f ю + TTW Gs (t) ■ (14-I0)
Даже в случае, когда автокорреляционные функции, соответствующие быстрым (f) и медленным (s) движениям, являются экспоненциальными [Gf = exp(—T/xf); Gs = exР(—T/Xs)], суммарная функция G(t) отвечает процессу с однородным распределением времен корреляции.
Скорости релаксации определяются следующими общими соотношениями [595]:
Ri = KDI, Q)[2I (<О) +8/ (2ш)];
(14.11)
^2=^D«3)[3/(0)+5/(ш)+2/(2(0) ],
-j-oo
Где Kd(Q) определены согласно (14.3), а /(со) = / б(/)ехр(—Mt)dt.
—оо
|
5а N, 3 S2 |
|
(14.12) |
В частности, из (14.10) и (14.11) при условии т/’Сюо-Ста несложно получить [580]:
Лх — 20іСх,«» (і + -п^ітг]
/?2 = 20^(Q)[(l—n^7r)xf4
10(1 +Л2/3) AR = R2 — RX=6KD<Q)Shs/(L+R2/3).
Таким образом, отличие времен релаксации Ті и Т2 для ориентационно-упорядоченной воды в пределе (OoTf<^Cl объясняется вкладом медленных движений.
Обычно при интерпретации релаксационных данных используют приближение быстрого мультифазного обмена между дискретными состояниями — свободной (F) и связанной (В) водой:
R = PPRF + PBRB, (14.13)
Где Pf и рв — доли свободной и связанной воды, а скорости релаксации Rf и RB описываются соответственно выражениями (14.1), (14.2) и (14.12).
Справедливость данного приближения оправдывается тем, что коэффициент самодиффузии воды в поверхностном слое является сильно анизотропным (D|,»Dj_). Авторы [580] на основании релаксационных данных для воды на ядрах 170 в дисперсии Si02 пришли к выводу, что £)„ на 1ч-2 порядка, a D± на 2ч-3 порядка ниже, чем D0 для объемной воды. Время Xbs, Со
Ответствующее медленным движениям для дисперсии коллоидных сферических частиц, выражается как [580].
T-‘s^T-‘res + T-‘iat + T-1*, (14.14)
Где Тгез=Я,2/(3£) і)—время жизни в состоянии В; X — толщина граничного слоя; Tiat=^?2/(6D||); R — радиус коллоидной частицы; TK=1/Ј>r; Dr — коэффициент вращательной диффузии коллоидной частицы.
Обобщенная двухступенчатая модель релаксации анизотропно-упорядоченной воды успешно использована для интерпретации релаксационных данных на ядрах 2Н и 170 в растворах полимеров и биополимеров [39, 605]. В [603] релаксационные данные на ядрах 1Н, 2Н и 170 анизотропно-упорядоченной воды в упорядоченных бислоях лиотропного жидкого кристалла интерпретируются с помощью другой теории, основанной на модели аксиального анизотропного вращения. Данная теория, первоначальный вариант которой был предложен Д. Восснером [606], позволяет объяснить наличие второго минимума на кривой зависимости Гі(тс) для протонов (см. рис. 14.2). Однако, как отмечено в [591], попытка использовать только этот механизм для интерпретации данных по протонной релаксации наталкивается на серьезные затруднения.
Системы с пониженной размерностью. Обычные теории межмолекулярного вклада в протонную магнитную релаксацию, предложенные для трехмерных систем, не применимы для систем с пониженной размерностью, например для одномерных (Ш) или двумерных (2D) систем. Вместе с тем при исследовании структуры воды в гидрофильных объектах системы такого типа встречаются довольно часто; например, вода, адсорбиро — ьанная на плоской подложке, вода между плоскими пластинками слоистых силикатов или вода в плоских бислоях лиотроп — ных жидких кристаллов — все это характерные примеры 2D — систем. Обзор теорий магнитной релаксации для систем с пониженной размерностью дан в работе [607]. Интересной особенностью неограниченных систем с пониженной размерностью является то, что для них функция спектральной плотности при малых частотах расходится и 1(ю-»-0)->оо. Для ограниченных систем (когда величина d на рис. 14.1 конечна) расходимости при малых частотах нет, но для таких систем на кривой зависимости Ті(тс) наблюдаются два минимума, соответствующие условиям <00ТС«1 и G)oTlat«l, ГДЄ Tlat«^2/(4D,|). ДеТЭЛЬ — ное обсуждение экспериментальных результатов по ЯМР релаксации в ограниченных двумерных системах приведено в работе [608].
Эффекты, связанные с неоднородностью магнитной восприимчивости в гетерогенных системах. Неоднородные магнитные поля, которые неизбежно возникают в гетерогенных системах вследствие разности магнитных восприимчивостей воды и гетерогенного объекта (Д/), приводят к уширению линий ЯМР воды (называемому неоднородным), их смещению, искажению формы, а также оказывают влияние на измеряемые времена магнитной релаксации [578, 609—616].
Можно выделить два основных фактора неоднородного уши- рения линий ЯМР воды в гетерогенных системах — пространственный и ориентационный [610]. Пространственный фактор уширения обусловлен пространственным распределением неоднородных магнитных полей в области гетерогенной системы, заполненных водой. Этот фактор для неоднородностей сферической формы и системы параллельных цилиндрических волокон детально проанализирован [611]. Для внешней жидкости в дисперсии сферических частиц линия ЯМР имеет гауссову форму, а ее полуширина равна
Avsphet=Avout « 8,82а | Ax I v0, где а—объемная доля сферических частиц в дисперсии.
Ориентационный фактор уширения обусловлен тем, что величина магнитного поля внутри неоднородности анизотропной формы зависит от ее ориентации в пространстве. Детальный анализ ориентационного фактора уширения проведен в [612] для модельной системы с неоднородностями сфероидальной формы. Спектр ЯМР может иметь довольно сложную структуру, вид которой определяется ориентационной функцией распределения неоднородностей в объекте и ориентацией объекта в магнитном поле. Общая протяженность спектра, обусловленная этим фактором, равна
AVVt ~ 12,57(ип — гс_і_)дх^о,
Где пц и п^ — коэффициенты размагничивания сфероида вдоль его длинной оси и перпендикулярно к ней.
В средах с анизотропией магнитной восприимчивости величина неоднородного уширения определяется также ориентацией микрокристаллитов в пространстве [609].
Для сужения неоднородно-уширенных линий используют метод согласования восприимчивостей, в котором для уменьшения Д/ пространство между частицами заполняют инертной жидкостью (не смешивающейся с водой и слабо взаимодействующей с поверхностью, например ССЦ) [613], или метод вращения под магическим углом СО скоростью Vrotj^Avhet [614]. Неоднородное уширение может также уменьшаться или сниматься полностью вследствие интенсивного диффузионного движения молекул воды [614]. Это происходит, если размер магниТных неоДнородно — СТЄЙ меньше ПО порядку величины, чем lc~~/D/ (АHet) « 1 мкм.
Полуширину диффузионно-суженной линии можно оценить с помощью соотношения
AVav ~ (Avhet) 2Т/, где Т, ~ /2/(6D).
Отметим, ЧТО Avaa~Vo2, ТОГДЭ как Avhet~v0.
Экспериментально показано [615], что время поперечной релаксации воды на ядрах ‘Н и 2Н в дисперсии стеклянных шариков определяется эффектами неоднородности магнитной восприимчивости. Гетерогенный вклад в скорость релаксации при использовании последовательности Карра — Парселла для измерения Тг можно оценить с помощью следующих соотношений:
Т~’2Ш « (nViej^VhetT)^-1 при (14.15)
F-‘zhet ~ (AvWr)2*, при I < lc, (14.16)
Где т — время между 180°-ными импульсами в последовательности.
Для последовательности 90°—т/2—180° т следует заменить на Гг. Квадратичная зависимость Г-12het от т экспериментально подтверждена в [615]. Для свободно-дисперсных систем может также проявляться гетерогенный вклад в Г2, связанный с диффузионным движением микрообластей [616].
Коэффициент самодиффузии. Для измерения самодиффузии воды в гетерогенных системах используется метод импульсного градиента (ИГ-ЯМР) [617—619]. При этом определяется макроскопический коэффициент диффузии D, так как минимальное время наблюдения за системой в данном методе (минимально возможное время между импульсами) превышает Ю-4 с. Связь между D и микроскопическим коэффициентом самодиффузии Dо определяется условиями диффузии в средах со стерическими препятствиями [620]. Для хаотически распределенных сферических препятствий [621]:
D~D0(l —а)3’2, (14.17)
Для плоскопараллельных препятствий (см. рис. 14.1):
D± ~ (A/rf)2D,| < D0) (14,18)
Анизотропия макроскопического коэффициента самодиффузии, связанная с эффектом препятствий, наблюдалась экспериментально для воды в упорядоченных гетерогенных системах [619, 621—623]. Эта анизотропия может проявляться даже в случае, когда микроскопический коэффициент диффузии изотропен (D0|I=D0±). При использовании метода ИГ-ЯМР важно также учитывать эффекты пространственно ограниченной самодиффузии, которые могут приводить к искажению измеряемых величин D [617].
Для измерения микроскопического коэффициента самодиффузии в некоторых работах [622, 623] использовали метод неупругого рассеяния нейтронов (НРН). Время наблюдения для данного метода составляет 10~12 с. Полученные с помощью ЯМР и НРН величины Dqb для граничной воды приблизительно на порядок ниже величин D0F для объемной воды [620].
 24 октября, 2012
24 октября, 2012  admin
admin 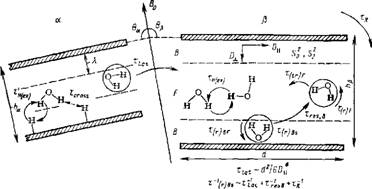
 Опубликовано в рубрике
Опубликовано в рубрике 