В использованных выше термодинамических соотношениях фигурировала обратимая поверхностная работа ст, которая совпадает с поверхностным натяжением 7 лишь в случае жидких поверхностей. Различие между а и у в случае твердых поверхностей, на которое впервые указал Гиббс [8], было представлено Шаттльвортом [98] для случая изотропной поверхности в виде
У = а + (даId In S)T (69)
Где 5 — площадь поверхности твердого тела.
В теории электрокапиллярности различие между у и а длительное время не учитывалось, прежде всего, по-видимому, по той причине, что достоверные экспериментальные данные о поверхностном натяжении твердых электродов отсутствовали.
Это различие было продемонстрировано Гохштейном, который развил метод эстанса — метод определения зависимости величины [ Dy/DQ‘ | от потенциала электрода [99—103]. Так как
Ду____ ду_ дЕ_ _ _ду_ ,7т
DQ‘ ~ дЕ dQ‘ ~ С дЕ к ‘
Где С — емкость электрода, то из | DyldQ‘ | легко рассчитать | ду/дЕ |.
Гохштейн показал, что ду/дЕ подчиняется уравнению:
Ду/ДЕ =— —Q’ — (dQ’/d In S)E (71)
Справедливость этого уравнения была подтверждена путем сопоставления величин (ду/дЕ)3 и (дЕ/д In S)Q‘, Т. е. на основе соответствия между изменением поверхностного натяжения при изменении потенциала и изменением потенциала при упругой деформации электрода.
Относительный вклад членов, входящих в йравую часть уравнения (71), в величину ду/дЕ зависит от природы металла, состава раствора и потенциала электрода. Так, в случае свинца в растворе фторида натрия | Q | > (DQ/D In S)|Ј. В то же время для кадмия и. особенно, платины роль второго члена в правой части уравнения (71) оказывается значительной.
На рис. 7 сопоставлены производные ду/дЕ и да/дЕ для платины в 1 н. H2S04 [102, 103]. Величины ду/дЕ были получены методом эстанса, DaldE приравнивалось полному заряду —Q‘.
|
Рис. 7. Различие между поверхностным натяжением Y и обратимой поверхностной работой о на уровне производных этих величин для платины в 1 н. H2S04 [ 102J 103]. |
Видно существенное различие между сравниваемыми величинами. Сопоставление показывает, что форма ду/дЕ, ^-кривой определяется, в основном, производной DQ‘/д In 5.
|
Dy — — |
Если твердый электрод находится в растворе, включающем т электронейтральных компонентов, то при условии Г^ = 0 для полного дифференциала у справедливо соотношение [102]
Dnk (72)
Где k, I = 1, …, m.
Некоторые вопросы влияния деформации сдвига на поверхностное натяжение и краевой угол смачивания твердых электродов были рассмотрены в последнее время Русановым [104].
ЗАКЛЮЧЕНИЕ
Итак, к настоящему времени достигнуты существенные успехи в термодинамическом описании электрокапиллярных явлений как на идеально поляризуемых, так и на обратимых
электродах. Важную роль при этом сыграла формулировка обобщенного понятия о заряде электрода, позволившая построить последовательную теорию электрокапиллярности для разнообразных электрохимических систем. Были найдены пути и указаны целесообразные формы соотношений для экспериментальной проверки термодинамической теории обратимых электродов. Тщательная проверка показала справедливость термодинамической теории и плодотворность вытекающих из термодинамического анализа методов исследования границы электрод—раствор.
На примере развития теории электрокапиллярности мы еще раз убеждаемся в разнообразии вопросов термодинамики поверхностных явлений, которые могут быть решены на основе адсорбционного уравнения Гиббса.
Автор приносит благодарность проф. А. И. Русанову и проф. Б. Б. Дамаскину за ценные замечания, сделанные при просмотре рукописи.
 2 января, 2013
2 января, 2013  admin
admin 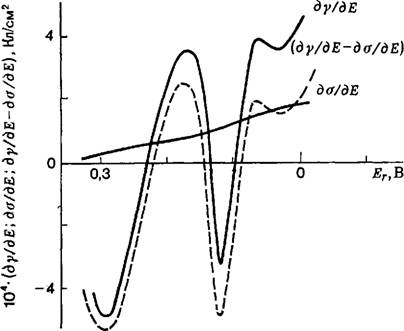
 Опубликовано в рубрике
Опубликовано в рубрике 