Уравнения (32) и (33) справедливы при произвольном положении математической поверхности Z — 0. Интегралы у, Г, т) и K меняются при каждом выборе разделяющей поверхности так, чтобы уравнения (32) и (33) оставались справедливыми. Таким образом, выбор положения этой поверхности — исключительно вопрос удобства; следуя Гиббсу, мы хотим выбрать ее так, чтобы упростить вид макроскопических граничных условий. При таком выборе существенно руководствоваться тем, чтобы плоскость 2 = 0 проходила через зону максимальной анизотропии межфазной поверхности и Az могла быть выбрана маленькой (Az 10~7ч-10~6см), а величины 0 (Аг) в уравнениях (32) и (33) были пренебрежимо малыми. Такой выбор должен также помочь интерпретировать величины типа
П
In „I
I Pzz = Pzz — Ргг
I
Как вычисляемые из свойств объемной фазы, экстраполированных по обе стороны оптически наблюдаемой межфазной поверхности. Если к тому же при переходе через анизотропную область мы сможем выбрать плоскость 2 = 0, чтобы сделать один из четырех интегралов у, Г, q, k равным нулю, то уравнения (32) и (33) еще более упростятся.
Чтобы проиллюстрировать такой подход, рассмотрим интеграл 7, определенный уравнением (27). Предполагаемый вид подынтегрального выражения изображен на рис. 5, где разделяющая поверхность 2 = 0 выбрана лежащей вблизи области максимума анизотропии межфазной поверхности. Разумное экспериментальное значение статического поверхностного натяжения -~50 эрг/см2; и из анализа интеграла Баккера (5) следует, что для Az ^ 5-Ю-7 см отличие рп от Pt в межфазной области —100 ат.
Таким образом, разность между двумя кривыми рп и Pt В зоне анизотропии очень велика. Тем не менее мы могли бы выбрать 2 = 0 так, чтобы интеграл (27) обращался в нуль при смещении точки разрыва функции Хэвисайда достаточно далеко влево, глубоко внутрь фазы I. Размер такого необходимого смещения зависит от амплитуды скачка функции Хэвисайда, изображенного на рис. 5. Для статической плоской межфазной поверхности известно, что р1 = рп, так что скачок функции Хэвисайда равен нулю; из этого следует, что для такой межфазной поверхности невозможно выбрать разделяющую поверхность так, чтобы 7 = 0. Для движущейся межфазной
Р
|
Z=0 z Рис. 5. Сравнение диффузной экспериментальной межфазной поверхности с моделями, приведенными на рис. 3. Интеграл V из уравнения (27) равен заштрихованной площади. Для нарисованной разделяющей поверхности поверхностное натяжение V положительно, иа его можно сделать равным нулю достаточно большим смещением плоскости г — 0 влево. |
Поверхности разность рп —Р1 может быть порядка (л11Э11 — (х1©1 10"8 атм; это означает, что смещение влево разделяющей поверхности на рис. 5 должно быть —1010 см, чтобы обеспечить равенство у нулю! Такая модель явно абсурдна.
Условие выбора выявляется из эвристического рассмотрения свойств вещества в объемной фазе. Для большинства экстремальных значений давлений и температур, достижимых в земных лабораториях, значение плотности конденсированных жидкостей меняется лишь в пределах одного порядка: от р яу 1 г/мл для углеводородов до р ^ 10 г/мл для жидких металлов. При тех же значениях температур и давлений значение сдвиговой вязкости • объемных фаз жидкостей меняется на много порядков: от р, « Ю-2 Пз для легких углеводородов до р « 107 Пз для таких материалов, как асфальт. Из этого следует, что вязкость вещества значительно более чувствительна к деталям внутренней структуры, чем плотность, и что какими бы ни были физические условия в межфазной области, они не могут быть столь экстремальными, чтобы р прошло через острый максимум или минимум при пересечении межфазной поверхности.
Теоретические попытки [17] описать плотность в переходном слое подтверждают эти эвристические аргументы; именно поэтому плотность р на рис. 4, а изображена, в виде монотонной линии. Даже в присутствии адсорбированных слоев поверхностно-активных веществ нельзя ожидать, что функция р, не являясь более обязательно монотонной, проявит ярко выраженные нерегулярности в анизотропной зоне.
Те же признаки позволяют нам с достаточным основанием предполагать, что у некоторых межфазных поверхностей (особенно содержащих адсорбированные слои) локальная структура окажется такой, что заставит значения вязкостей к, А/, р, р’, р" резко измениться по сравнению со значениями в объемной фазе. Именно по этой причине кривая р’ на рис. 4, б изображена с резким максимумом.
В принципе, возможно выбрать разделяющую поверхность так, чтобы интегралы либо Tj (31), либо K (34) обращались в нуль. Но эти условия неудобны по той же причине, по которой неудобно требовать обращения в нуль интеграла у.
Следовательно, нам остается единственное реальное условие — выбрать плоскость 2 = 0 так, чтобы сделать интеграл Г в уравнении (30) равным нулю. Такой выбор не только обратит в нуль инерционные члены в левых частях уравнений (32) и (33), но к тому же предположенный нами и изображенный на рис. 4, а монотонный ход плотности гарантирует, что разделяющая поверхность пройдет через наблюдаемую в оптическом эксперименте межфазную поверхность.
Итак, толщину AZ можно выбрать столь малой, что это позволит исключить величины 0 (Аг) из уравнений (32) и (33). В результате получаем систему граничных условий, подходящую для гидродинамических задач, содержащих плоскую межфазную поверхность:
Нормальная составляющая — П
TOC o "1-3" h z | Pzz = — (Р11 — Р1) — 2 (ц11 — ц1) = 0 (35)
I
Тангенциальные составляющие —
+ Ј + + о
И (36)
Уравнения (36) совпадают с уравнением (2), если у, определяемая уравнением (27), экспериментально неотличима от у, Определяемой уравнением Баккера (5). Я полагаю, что дополнительное удобство выбора разделяющей поверхности из условия Г — 0 состоит в устранении какого-либо практического различия между двумя определениями поверхностного натяжения. Из уравнения (35) следует, что разность ри—Р1, равная — 2 (р11 — р1) 0°, для лрактически интересных в поверхностной реологии значений скорости дилатации 0° и вязкостей объемных фаз р,1, рп имеет порядок 10~10—10~в атм. При условии, что рп—pt в межфазной области примерно равна 100 атм, «ступенька» на рис. 5, связанная с функцией Хэвисайда, в действительности очень мала. И поскольку этот скачок помещен в область максимума межфазной анизотропии, мы вправе интегралы (5) и (27) принять эквивалентными для определения поверхностного натяжения.
ЗАКЛЮЧЕНИЕ
Итак, мною показано, что математический метод Гиббса, столь успешно примененный им к статической межфазной поверхности, в равной степени применим к движущимся жидким межфазным поверхностям. В частности, моделирование межфазной поверхности математической плоскостью и выбор такого положения этой плоскости, что избыточная поверхностная плотность массы делается равной нулю, позволяют определить не только термодинамические величины (например, концентрацию адсорбированных поверхностно-активных веществ), но также и поверхностные реологические коэффициенты K и т}, т. е. коэффициенты поверхностной дилатационной и сдвиговой вязкости. Использование интегралов (30), (31) и (34) открывает дорогу теоретическому вычислению этих параметров методами неравновесной статистической механики.
Автор благодарит Национальный Научный Фонд (субсидия № СНЕ-7505240) за поддержку этой работы.
 29 декабря, 2012
29 декабря, 2012  admin
admin 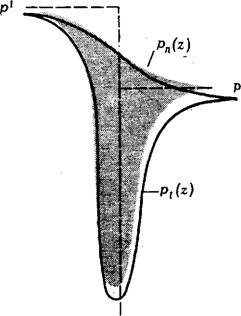
 Опубликовано в рубрике
Опубликовано в рубрике 