|
|
В качестве последней задачи рассмотрим липидные бислои в везикулах, размер которых настолько велик, что с эффектами кривизны можно не считаться. Ради простоты — ограничимся анализом симметричного случая. Если везикулярный бислой закрыт по отношению к липидному компоненту, то фундаментальное уравнение (16) должно быть в принципе применимо. Однако в случае везикулы поверхность мембраны уже не является независимой переменной, а будет функцией Т и р3. Если это обстоятельство учтено явно, то мы получаем фундаментальное уравнение в надлежащей для данного случая форме, а именно:
|
|
(61)
Пока еще ничего определенного нельзя сказать об относительных величинах (от —7т)-членов в уравнении (61). Однако ожидаемый порядок (Д In Лт/дТ)11з составляет Ю-4 град-1 по оценкам для чистой воды. К тому же из наших предыдущих рассуждений в подразделе, посвященном равновесному образованию бислойной липидной мембраны, следует, что разность | ат —ут | должна быть мала, скажем, порядка 1 эрг-см-2. Поэтому мы можем сделать оценку:
от-ут{дпАт1дТ)]1з < КГ4 эрг-(см"2-град"1) (62)
Два первых члена в коэффициенте при DT уравнения (61) содержат в основном разность энтропий одиночного бислоя и бислоя в ламеллярном стандартном состоянии. Сугубо приближенная оценка состоит в том, что эта разность составляет величину порядка КГ1—Ю-2 эрг-см"2-град-1. Следовательно, dT-член уравнения (61), вероятно, играет малую роль.
В экспериментальном отношении дифференциальные соотношения для ут, соответствующие уравнениям (18) и (19), представляют некоторый интерес:
Возможно, что в данном случае ^»"-содержащие члены имеют характер малых поправок. Так ли это в действительности или нет —должно быть установлено в дальнейших экспериментальных работах.
ЗАКЛЮЧЕНИЕ
На нынешней стадии развития важнейшая задача применения классической термодинамики к бислойным липидным мембранам, вероятно, состоит в исследовании экспериментальных возможностей и в разработке руководящих принципов выполнения эксперимента, на основании чего могла бы быть получена новая информация по термодинамическим свойствам бислоев. Из настоящего формального анализа видно, что особое значение имеет дальнейшая работа по развитию техники измерений натяжения мембран в сочетании с методикой формирования их, предложенной Тагаки и др. [14]. Уравнения (34), (38)—(40) говорят о том, что если монослойные свойства известны, то полная информация по термодинамическим свойствам бислоев может быть получена из измерений Ym (Т, Yf, р3) на открытой по отношению к соответствующей монослойной пленке бислойной липидной мембране.
Второй хорошей возможностью было бы проведение измерений зависимости ут от при переменных Т и р3 для частично закрытого бислоя, аналогичных пленочно-весовым измерениям на нерастворимых поверхностных пленках. В этом случае и уравнение (13) и (22) приложимы. Следует, однако, отметить, что потребуется интегрирование изотермы для того, чтобы найти все термодинамические свойства бислоя. Открытая по отношению к фазе органического растворителя бислойная мембрана, по-видимому, является менее удачной системой при отыскании необходимой термодинамической информации, в основном, из-за априорного присутствия органического растворителя в бислое.
Если говорить об исследованиях асимметричных бислойных мембран, то можно думать, что открытая бислойно-монослой — ная система, если вообще она реальна, предоставит определенные преимущества.
Автор хочет поблагодарить докторов Б. Тошева и Р. Кьел — ландера за ценные замечания при обсуждении этой работы.
[1] Gibbs J. W. — Proc. Amer. Acad., 1881, v. 16, p. 420.
[2] edz + I v’v*dz
[3] Харкинс и Браун построили калибровочную кривую для определения поверхностного натяжения методом веса капель, используя в качестве стандарта значения поверхностного натяжения жидкость— пар, измеренные независимо. Для системы жидкость—жидкость инерционные и вязкие эффекты значительны, так что нельзя полагаться на «принцип подобия» Харкинса между поверхностями жидкость— пар и жидкость—жидкость, т. е. результат Харкинса для у системы бензол—вода нельзя рассматривать как абсолютный.
Восилэит [26] использовал метод висящей капли, а Пиетрас [26] измерил поверхностное натяжение методом пластины Вильгельми с отделением пластины от поверхности.
[4] Десятичные логарифмы применяются для сохранения численных ве* личин констант работ [7, 8].
[7] J = + 1Д2, где К— составляющие радиусы кривизны межфазной поверхности.
[8] Т/Гсг
[9] Здесь и далее (Где заменяется на а.
[10] Чтобы получить отрицательный знак б2Sc^l, разделяющая поверхность должна быть выбрана так, чтобы Г>- 0.
[11] Glansdorff P., Prigogine /. Thermodynamic Theory of Structure, Stability and Fluctuations. N. Y., Wiley, 1971.
2. NicolisG., Prigogine I. Self-organization in Nonequilibrium Systems. N. Y., Wiley, 1977.
3. Sanfeld A., Steinchen-Sanfeld A. — Bull. Acad. Roy. Belg. CI. Sci., 1971, v. 57, p. 684.
4. Takeyama K-, Kitahara K. — J. Phys. Soc. Japan, 1975, v. 39, p. 125.
5. Matsushita M. — Ibid., 1976, v. 41, p. 674.
6. Defay R., Prigogine /., Sanfeld A. — J. Coll. Interface Sci., 1977, v. 58, p. 498.
7. Defay R., Prigogine /., Bellemans A., EverettD. H. Surface Tension and Adsorption. London, Longmans, Green, 1966.
8. Defay R. — Sortir de l’equilibre. Collection «Discours de la Methode» Gauthier-Villars. (in press).
9. BedeauX D., Albano^A. M., Mazur P. — Physica, 1976, V. 82A, p. 438.
10. Kovac J. — Ibid., 1977, v. 86A, p. 1.
[12] В работах [10—12] использовалось обозначение Gex для а с тем, чтобы подчеркнуть тот факт, что эта величина есть избыточная свободная энергия. В данном тексте мы придерживаемся системы обозначений Гиббса, наиболее употребительной сейчас [13].
[13] Строго говоря, здесь и далее речь будет идти не об асимметричных бислойных мембранах, а об асимметричных мембранных системах, включающих помимо мембраны еще и примыкающие к ней водные растворы. (Прим< Переводчика).
 4 января, 2013
4 января, 2013  admin
admin 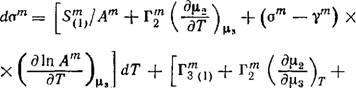
 Опубликовано в рубрике
Опубликовано в рубрике 