Королевский технологический институт Отдел физико-химии S-10044, Стокгольм, 70
Развит термодинамический формализм для бислойных липидных. мембран В контакте с водным раствором. Рассмотрены три класса симметричных бислойных липидных мембран: закрытые по отношению к липидному компоненту (I), открытые по отношению к монослойной липидной пленке (2), открытые по отношению к фазе липидного растворителя (3). Для всех этих типов липидных бислойно-мембранных систем выведены фундаментальные термодинамические уравнения, содержащие мембранное натяжение ут, формально соответствующие гиббсовскому уравнению для поверхностного натяжения.
Для частично закрытой бислойной липидной мембраны (I) также получено фундаментальное уравнение, подобное фундаментальному уравнению для твердых поверхностей, выведенному автором ранее. Это уравнение базируется на работе образования бислойной мембраны от из насыщенного водой ламел — лярного липидного жидкого кристалла, выбранного в качестве стандартного состояния.
Корреляции между монослойным состоянием липида с поверхностным давлением, близким к равновесному давлению растекания, и соответствующим, бислоем исследуются на приближенной основе, существенным элементом которой является использование мембранной модели Давсона — Даниели.
Коротко рассмотрена термодинамика асимметричных бислойных липидных мембран. Обсуждается приложение полученных теоретических результатов для дальнейшей экспериментальной работы по термодинамике бислойных ли-,
Пидных мембран.
ВВЕДЕНИЕ
Липидные бислои, широко используемые в качестве моделей биомембран, в последние годы интенсивно исследуют с применением различных экспериментальных подходов [1, 2]. В част=- ности, разработаны методы измерения натяжения бислойных мембран, обеспечивающие получение важной информации о термодинамических свойствах липидных бислоев. Цель настоящего сообщения — развитие строгого и полного термодинамического формализма для бислойных липидных мембран.
Предшествующие исследования, относящиеся непосредственно к термодинамике липидных бислоев, включают работы Тьена [3], Гуда [4], Эванса и Саймона [5], Эванса и By [6]. Тошев и Иванов недавно обратились к близко примыкающей проблеме тонких жидких пленок между двумя жидкостями [7, 8]. Известная (но во всех деталях еще не всегда хорошо понимаемая) теория капиллярности Гиббса [9, стр. 219] и предыдущие статьи автора данной серии работ по поверхностной термодинамике, в частности сообщения [10—12] обеспечивают подходящую общую основу, которой мы и воспользуемся.
В зависимости от окружающей температуры и экспериментальных особенностей, определяющих возможности массопере — носа, бислойная липидная мембрана является фактически либо Частично закрытой, либо открытой термодинамической системой. Как отмечалось Гиббсом [9] и показано явно для твердых поверхностей [10, 12, 13] и нерастворимых поверхностных пленок [11], термодинамику закрытых или частично закрытых поверхностных систем следует развивать в направлении, отличном от обычно используемого для полностью открытых поверхностных систем. Результирующие фундаментальные уравнения также обладают отличной природой. По существу —это следствие необходимости явного учета изменений состояния, обусловленных изменениями поверхностной деформации.
Как будет показано ниже, продольная деформация мембраны может быть выбрана в качестве независимой переменной состояния для частично закрытой бислойной мембранной системы, что приводит к фундаментальному уравнению типа уравнения Шаттлворта, подобно тому, как это сделано в случае нерастворимых поверхностных пленок. С другой стороны, введение деформационно-зависимого химического потенциала для мембрано — образующего липида в бислое позволяет почти полностью следовать гиббсовскому методу, приводящему к фундаментальным уравнениям гиббсовского типа. Полностью открытая бислойная мембрана может быть рассмотрена непосредственно в рамках гиббсовского метода. Ниже мы покажем, что открытые би — слойномембранные системы представляют также определенные преимущества для извлечения желаемой термодинамической информации о составе мембраны, энергии, энтропии и т. д.
ОПИСАНИЕ ИССЛЕДУЕМОЙ ЛИПИДНОЙ БИСЛОЙНО-МЕМБРАННОЙ СИСТЕМЫ
По большей части мы рассматриваем плоскую, симметричную липидную бислойную мембрану, образованную одним водо- нерастворимым липидным компонентом, например лецитином (компонент 2), погруженную в воду (компонент 1) в присутствии одного растворимого компонента, например, соли поверхностно — активного вещества или белка (компонент 3). Обобщение на случай многокомпонентного водного раствора —тривиально; в случае же двух или более мембранообразующих компонентов оно также просто для открытой бислойной мембраны, но нуждается в специальном исследовании для частично закрытых бислойных мембран.
Температуру всегда выбирают выше температуры Тс перехода гель — жидкий кристалл (Чепмен), что позволяет считать продольную (но не поперечную) диффузию в бислое относительно быстрой и, кроме того, изотропными в продольном направлении все термодинамические свойства бислоя. Давление в основном предполагается равным атмосферному. Поэтому можно пренебречь вкладом от рУ-членов в термодинамические свойства мембранной системы и отпадает необходимость различия свободных энергий Гельмгольца (F) и Гиббса (G). Неявно это также означает, что вопрос о том, как реализуется механическое равновесие на границах бислоя, исключается из рассмотрения.
Точные границы термодинамической бислойно-мембранной системы по отношению к водному раствору могут быть условно определены посредством пары гиббсовских разделяющих поверхностей 2(1), размещенных так, что избыток воды (компонент 1) для каждой из сторон мембраны обращается в нуль (рис. 1). Неявно мы тем самым делаем резонное предположение, что локальная концентрация воды в центральной части мембраны относительно мала. Толщина мембраны определяется как расстояние между двумя разделяющими поверхностями 2(i).
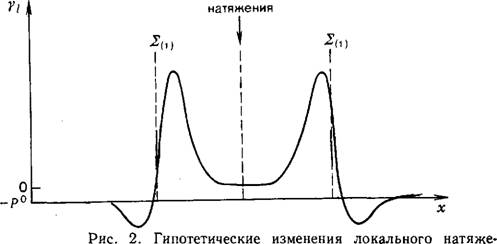
Пусть, кроме того, профиль локального натяжения по толщине мембраны соответствует рис. 2. Таким образом, при растяжении в бислое возникает результирующее, так называемое мембранное натяжение ут. Для симметричной бислойной мембраны поверхность натяжения локализована, очевидно, посредине между разделяющими поверхностями 2(1).
Энергию t/«)f энтропию Sft,, свободную энергию и число молей nf(1), липидной бислойно-мембранной системы вычисляют с использованием обычного условия Гиббса, как показано нижним индексом (1). Соответственно водная фаза предполагается строго неизменной вплоть до разделяющих
|
Рис. 1. Определение толщины бислойной липидной мембраны посредством двух гиббсовских разделяющих поверхностей 2(0- СJ — концентрация воды; х — координата по нормали. Поверхность |
|
Ния Y2 растянутой бислойной мембраны. Площадь под кривой соответствует результирующему мембранному натяжению ут. Давление окружающей среды Р0. |
Поверхностей 2(i). Очевидно, что из-за ничтожной растворимости мембранообразующего липидного компонента в воде ^го) = или> иными словами, величина пf нечувствительна к. смещению положения обеих разделяющих поверхностей.
|
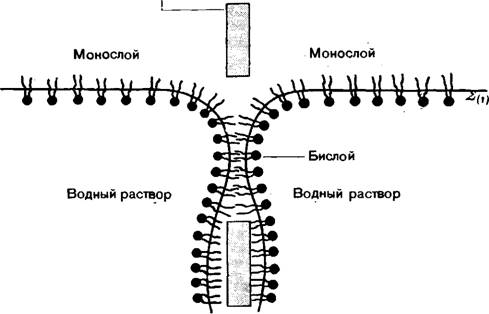
Гидрофобная подложка с отверстием
Рис. 3. Приготовление бислойной липидной мембраны из соответствующего монослоя согласно методу Такаги и др. [14]. |
В общем, описанное выше термодинамическое состояние бислойной липидной мембраны является закрытым по отношению к липидному компоненту 2 и определяется тремя степенями свободы. В качестве независимых переменных состояния мы можем выбрать температуру и химические потенциалы липид — ного компонента в бислойной мембране pf и растворенного в воде вещества р3. Вместо p. f за независимую переменную можно принять площадь мембраны Ат (мембранная деформация ГТ _ дт/дт0) или мембранное натяжение ут.
 4 января, 2013
4 января, 2013  admin
admin 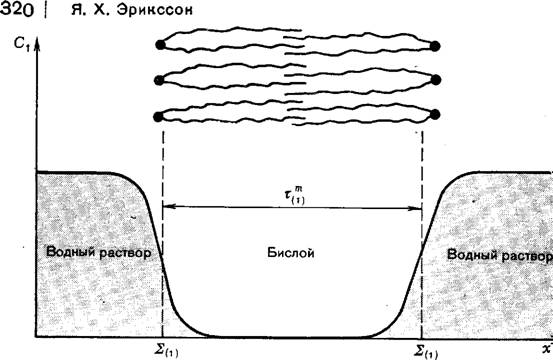
 Опубликовано в рубрике
Опубликовано в рубрике 