Оценка толщины поверхностных слоев
Во времена Гиббса практически отсутствовали сведения о толщине поверхностных слоев и можно было только предполагать, как это делал Гиббс, что эта толщина очень мала ввиду
малости радиуса действия молекулярных сил. Поэтому Гиббс стремился сформулировать такой термодинамический метод, в котором не фигурировала бы толщина поверхностных слоев. К настоящему времени, однако, известен целый ряд методов исследования толщины поверхностных слоев (см. обзор [41, стр. 57—114)], уже получены интересные экспериментальные и теоретические результаты в этой области. Оказалось, что и термодинамика может дать определенные сведения о толщине поверхностных слоев. На первый взгляд это кажется удивительным: ведь метод слоя конечной толщины эквивалентен методу Гиббса, основное уравнение метода слоя конечной толщины — уравнение (13) — справедливо при произвольной толщине поверхностного слоя и, следовательно, не может дать сведений об этой величине. Однако положение меняется, если принять во внимание не только условия равновесия, к которым, относится уравнение (13), но и условия устойчивости, выражаемые термодинамическими неравенствами. В самом деле, если мы рассматриваем поверхность разрыва как реальное физическое тело, мы должны принять, что она удовлетворяет условиям устойчивости. Одним из них является условие устойчивости поверхностного слоя в отношении его толщины, т. е. способность поверхностного слоя восстанавливать свою равновесную толщину при ее случайных изменениях. Строго говоря, под этим понимается способность поверхностного слоя устойчиво сохранять молекулярную структуру и профили всех его локальных свойств.
|
|
Условие устойчивости поверхностного слоя в отношении его толщины можно выразить неравенством [20, стр. 49 и 42]
(46)
Где Е’ — условный модуль упругости поверхностного слоя; а — поверхность, приходящаяся на единицу массы поверхностного слоя; производная берется при постоянстве температуры, внешнего давления и состава поверхностного слоя; о — поверхностное натяжение.
|
|
Применительно к бинарной системе условие (46) позволяет доказать неравенство [42; 18, стр. 151]
(47)
Где и х^ — молярная доля одного из компонентов в поверхностном слое и объемной фазе.
Неравенство (47) является аналогом третьего закона Коновалова для равновесия жидкость—пар, оно интуитивно воспринимается и без доказательства. Кроме того, имеется очевидное неравенство:
О < < 1 (48)
Определяемая из опыта величина относительной адсорбции П (2) может быть однозначно связана с величиной х°, если задана толщина поверхностного слоя т. Поэтому условия (47) и (48) накладывают ограничения на толщину поверхностного слоя. Для систем жидкость—газ и жидкость—твердое тело эти ограничения выражаются неравенствами (в приближении несжимаемой жидкой фазы) [43]
(49)
ОоЛ (2) (50)
Где у® — молярный объем жидкой фазы;
V01 — молярный объем первого компонента в жидкой фазе.
Знак равенства в (49) и (50) указывает минимальное возможное значение толщины поверхностного слоя как функцию состава раствора.
Таким образом, хотя термодинамика не может указать истинную эффективную толщину поверхностного слоя, она позволяет определить нижнюю границу возможных значений толщины. Применение неравенств (49) и (50) к экспериментальным данным о поверхностном натяжении и адсорбции показывает, что минимальная возможная толщина может оказаться весьма малой (меньше молекулярных размеров) и в таком случае эти неравенства мало информативны, но в других случаях минимальная возможная толщина оказывается заметной и даже значительной. В частности, этим методом было установлено сильное возрастание толщины поверхностного слоя на границе жидкость—газ при приближении к критической точке расслаивания жидкого раствора [41, 44].
 28 декабря, 2012
28 декабря, 2012  admin
admin 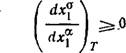
 Опубликовано в рубрике
Опубликовано в рубрике 