Сто лет назад Гиббс создал термодинамическую теорию капиллярности в виде существенной части его третьей работы — термодинамики гетерогенных систем [1 ]. Эпиграф из Клаузиуса о том, что энергия вселенной постоянна, а энтропия ее стремится к максимуму, подчеркивает масштабы этой работы.
Использованный, однако, метод описания гетерогенных систем через макроскопические параметры, определяющие равновесие фаз, создает трудности для ее применения к очень малым фазам.
В разделах «О возможности образования отличной по фазе жидкости внутри гомогенной жидкости» [1, стр. 252—258] и «Жидкие пленки» [1, стр. 300—314], где предметом исследования являются малые капельки и тонкие слои жидкости, Гиббс специально ограничивается такими размерами фаз, когда в них еще сохраняется вещество, которое можно рассматривать как веществе некоторой-фааы в, массе. Именно для таких достаточно больших капель и достаточно толстых пленок Гиббс предлагает окончательные решения. Для меньших фаз он ограничивается лишь советами о том, как их следует термодинамически рассматривать. Эти рекомендации в той или иной степени реализованы, например, путем применения введенного Дерягиным [2] представления о расклинивающем давлении в тонких пленках, и поэтому мы их здесь не рассматриваем. Гиббс останавливается также и на вопросе о переходе к нулевым фазам — в нашем представлении к фазам молекулярных размеров, относительно которых он считает, что полученные для больших фаз уравнения «вряд ли будет иметь смысл пытаться истолковать» [1, стр. 255].
Казалось бы, что при таких ограничениях проблемы возникновения новой фазы из, например, пересыщенных паров решить термодинамическим путем невозможно, поскольку подобная фаза образуется за счет нарастания, начиная с молекулярных размеров.
Важной заслугой Гиббса является то, что он показал несостоятельность такого полного ограничения. В результате подробного анализа состояния пересыщенных систем (пересыщенного газа, например) Гиббс показал, что устойчивость системы (и кинетика фазообразования) определяется капельками такого размера, при котором давление ее паров Рг равно давлению паров пересыщенной системы, т. е. капельки зародыша новой фазы имеют размеры значительные по сравнению с молекулярными при не очень больших значениях пересыщения (Рг —
Связь Рг и дается уравнением Томсона—Гиббса
Где Роо — давление паров очень большой капли; а — поверхностное натяжение; v — молекулярный объем жидкости в капле; R — радиус капли; K И Т — постоянная Больцмана и абсолютная температура.
Уравнение (1) справедливо, когда газовая фаза идеальна, а жидкая несжимаема.
Работа образования такого зародыша равна
W = aS — Pav = —I— aS (2)
Где S — поверхность сферического зародыша; V — его объем.
Капиллярное давление в нем-
Ра = 2O/R (3)
Является энергетическим барьером образования новой фазы, который сохраняется в этом виде во всех кинетических теориях о скорости зарождения новой фазы, развитых после Гиббса.
Измерения Фольмера и Флуда [3] по образованию тумана в камере Вильсона показали, что теория скорости образования тумана удовлетворительно согласуется с экспериментом, хотя размеры зародышей, вычисленные по формуле (1) для исследованных пересыщений, очень малы: для воды они соответствуют 72 молекулам; для метилового спирта — 27; для пропилового спирта — 114; для изопропилового спирта — 119; для бутилового спирта — 74; для нитрометана — 64; для этилацетата — 41. Из этого следует, что макроскопическое термодинамическое описание малых капель допустимо для агрегатов до нескольких сот и даже десятков молекул.
Итак, проблема очень малых фаз может быть приближенно обойдена в термодинамической части теории гомогенного образования новой фазы при достаточно малых пересыщениях.
Не так, однако, обстоит дело с гетерогенным образованием новой фазы, если придерживаться теории Гиббса, изложенной в разделе «О возможности образования в поверхности, где соприкасаются две различные гомогенные жидкости, новой отличной от них жидкой фазы» [1, стр. 258—264], и не учитывать сделанные им критические замечания.
В этой теории рассматривается жидкая капелька — линза С, находящаяся в термодинамическом равновесии между жидкими фазами А и В, которые встречаются в плоской поверхности. Как и в предыдущем случае, поверхности капли С сферичны. Углы контакта по отношению к плоской поверхности АВ Гиббс получает, выводя для этой цели, силовым путем, правило, позднее названное правилом Неймана.
Работа образования такой капли-зародыша, т. е. капли, давление паров которой равно давлению в пересыщенной этими парами фазе А или В, получается такого же вида, что и для гомогенного образования новой фазы, а именно:
°iSi — Pav = — у I <*iSi (4)
Здесь ]T]cF, Sj — изменение свободной поверхностной энергии
В системе при появлении в ней линзы новой фазы С с объемом V. Для специального случая линзы на плоской твердой поверхности формула (4) дает:
W2 = — i — — 3 cos 9 +cos3 6) (5)
Здесь применено правило Юнга, которое является частным случаем правила Неймана, для капли, смачивающей плоскую поверхность под углом 9.
Эту формулу, впервые выведенную Фольмером [4], используют для описания термодинамической части теории гетерогенного образования новой фазы на твердой подкладке и на ядрах конденсации.
Между тем Гиббс серьезно критикует формулу (4) [1, стр. 261 ]: «Надо, однако, заметить, что в непосредственном соседстве круга, в котором пересекаются поверхности разрыва, физическое состояние каждой из этих поверхностей должно зависеть от соседства других. Мы не можем поэтому полагаться на формулу (4), за исключением тех случаев, когда размеры линзообразной массы имеют заметную величину».
Это замечание Гиббса относится и к формуле (5), а также и к правилам Неймана и Юнга, как мы далее покажем. Интересно заметить, что нижний предел применимости (4) по размерам Гиббс не ограничивает ни молекулярными размерами, ни наличием в капле вещества со свойствами большой фазы, хотя во всех других случаях, когда речь идет об очень малых фазах, такая оговорка делается. По-видимому, Гиббс имел в виду не особенности малых фаз в этом смысле, а то, что в трехфазной системе необходимо учитывать и линейные параметры, отсутствующие в системе из двух фаз. В этом смысле идея о линейной термодинамике, сопряженной с дву — и трехмерной, в системе из трех фаз развивается подробно Гиббсом в примечании [1, стр. 288]: «Мы можем отметить здесь, что в теории равновесия и устойчивости можно достигнуть более близкого приближения, если в наших общих уравнениях специально принять во внимание линии, по которым пересекаются поверхности разрыва. Эти линии можно было бы трактовать по способу, совершенно аналогичному тому, которым мы трактовали поверхности разрыва. Мы могли бы ввести понятия о линейной плотности энергии, энтропии и отдельных веществ, которые присутствуют около этой линии, а также и определенное линейное натяжение».
Хорошо известно, что введение представления о линейном натяжении к автоматически приводит к возникновению двумерного давления (или натяжения) сгх при искривлении линии трехфазного контакта подобно тому, как представление о поверхностном натяжении связано с возникновением капиллярного давления Ра, когда поверхность раздела двух фаз искривлена.
На точки а и Ь, расположенные симметрично около пересечения нормали N с линией трехфазного контакта с радиусом г, действует натяжение к по касательной к этим точкам (рис. 1).
|
Рис. 1. Схема трехфазного контакта. |
Это натяжение образует силу 2х sin — в направлении, параллельном N. Тогда на единицу длины дуги Ab действует сила
2х
— sin ~Y . Двумерное давление (натяжение) для точки пере-
TOC o "1-3" h z Ab ._ ,
Сечения с N получаем при Ab —► О
П . 8а 2х Sin
Стх = Lim——— з—— = х lim = x/CL = — (6)
Ob->0 йЬ ab->0
поскольку lim (баLab) при аЬ0 равен кривизне линии KL = = Mr в этой точке.
Полученное выражение является полдым двумерным аналогом капиллярного давления Ра, а формула (6) — уравнения Лапласа: Ра = OKs, где Ks — кривизна поверхности. Подобный вывод члена х/r сделан Веселовскйм и Перцовым [5].
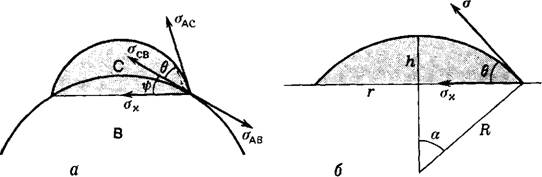
Следуя силовому выводу правила Неймана (и Юнга), надо добавить к балансу натяжений по периметру капли С между фазами А и В также и натяжение сги. В общем случае искривленной поверхности твердого тела, проводя этот баланс по отношению к касательной к этой поверхности, получаем (рис. 2, а):
|
280 I А. Шелудко, Б. В. Тошев, Д. Платиканов А
Рис. 2. Профиль капли, смачивающей искривленную поверхность твердого тела (а) и плоскую поверхность твердого тела (б). |
Термодинамический вывод (7) был сделан недавно одним из нас [6]. Для плоской поверхности подкладки В, когда = О, с учетом (6) получаем выражение
|
X |
|
= о |
|
(7а) |
ААВ — °АС Cos е — авс
Которое переходит в правило Юнга, когда радиус периметра смачивания достаточно велик и 0 = 0те — const:
|
(8) |
|
АВ |
ААс созею-авс = 0
Отсюда (7а) можно представить через угол смачивания 0< большого периметра смачивания в виде:
°ac (cos ~~ cos = х/г
Формулы (7), (7а) и (76) можно рассматривать как описывающие зависимость угла смачивания от периметра смачивания.
Формула (76) не совсем точна, так как равновесное давление паров в системе с малой и большой каплей не одинаковы, и, следовательно, и стАВ в обоих случаях различны, например, из-за адсорбции паров С на поверхности АВ. Поскольку, однако, изменение стАВ связано с адсорбционной способностью этой поверхности, можно выделить особенно простой случай, когда стАВ = const.
|
(76) |
Учет х при выводе работы образования зародыша на подкладке состоит в том, что к балансу энергий в формуле (4) добавляется линейная энергия xL, где L — длина периметра сма
чивания. Так, для капли на плоской твердой поверхности получаем [9]
W‘2=-J— лRza (2 — 3 cos 6 + cos3 6) + (9)
Последний член является работой образования двумерного зародыша. Ее можно получить отдельно, транспонируя формулу (4) от дву-трехмерной к одно-двумерной системе:
^двумерное = XL — CXS = xL/2 (10)
Здесь х соответствует a; L — 5, ах — Рр и 5 — V в выражении (10): L = 2яг; S = яг2 и стх = х/г.
Угол 0 в уравнении (9) — истинный угол смачивания капли зародыша и не равен 6 =*= 6те в выражении (5). Формула (9) была выведена сравнительно недавно Грецем [7].
Здесь мы обратим внимание на некоторые важные следствия из этой формулы.
Введем в (76) безразмерную кривизну
К = X/oR <и)
Что вместо (76) дает:
(Cos 0те — cos 6) sin 0 = К (7в)
Здесь r = ^sinana = 0 (рис. 2, б). Формула (7в) показывает, что смачивающая капля не может существовать при любых R и, соответственно, при любых пересыщениях, сохраняя при этом сферическую форму поверхности. Равенство (7в) выполняется только до некоторых предельных
/V
Значений /Сшах, соответствующих углам смачивания 9Ш. Решение для экстремума (7в) дает:
Cos 0_ ( / ft
= J (.2,
Угол ет меняется от 120° при 9те = 0° до 180°.при 9» = 180°. Соответственно максимальные значения К пробегают значения от 1,299 при 9те = 0° через 0,5 при б*, = 90° до нуля при 9те = = 180°. Так что исследование по фазообразованию линзы с уче-
А/
Том х следует проводить для 9 между 9,» и 9т или для К между 1,299 и нулем.
Для оценки влияния х на гетерогенное образование новой фазы полезна сопоставить результаты, полученные с учетом х и без такового, например:
W2 _ 2 — 3 cos 0 — f cos3 8 + Зх sin Q/oR „
Wt ~ 2-3cos0oo + cos30oo ( ‘
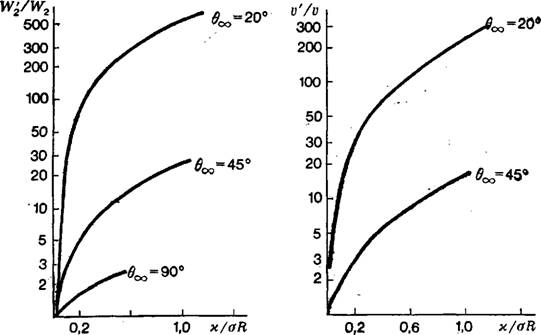
А — работы образования зародыша на подкладке, полученной с учетом линейного натяжения к работе образования такого же зародыша, но без учета W2, от безразмерной кривизны капли К = | к/oR | для трех углов смачивания 0^ большой капли; б — объема смачивающей капли полученного с учетом ли* нейного натяжения, к объему капли V, полученному без такого учета от безразмерной кривизны капли К = | м/oR | для двух углов смачивания 0 большой капли.
Здесь W* записано по формуле (5) с 0 = 0». Сочетая (13) с (7в), получаем: WyW2 = / (К). Эта обезразмеренная зависимость показана графически на рис. 3, а для трех значений в». Рис. 3, а показывает, что неучет к может привести к очень сильному занижению значения работы образования зародыша, особенно при
Малых углах смачивания 0» большой капли, даже когда К «С 1.
Очень значительную поправку вносит учет х и при вычислении объема зародыша из данных о пересыщении, соответственно о кривизне смачивающей капли-зародыша по формуле (1). Отношение при равной кривизне объема V‘ действительной капли к объему V капли, вычисленному без учета х, т. е. при 0 = 0W, дает:
|
Рис. 3. Теоретически вычисленная зависимость отношения: |
|
А б |
V’ (1 —cos0)2(2-f cos0)
Здесь 0 снова выражается через К согласно (7в) и зависимость V‘/V = F (К) есть мера ошибочности интерпретации объема зародыша без учета х.
Рис. 3, б, где результат решения уравнения (14) и (7в) иллюстрирован кривыми для двух значений 0*,, указывает на отклонение от фольмеровской зависимости по объему зародыша; это
Отклонение снова примерно экспоненциально возрастает с К, особенно сильно при малых углах смачивания Ос.
Итак, оставаясь в рамках макроскопической термодинамической теории образования новой фазы, для условий ее выделения на подкладке необходимо обязательно учитывать линейное натяжение.
Пренебрежение этим при гетерогенном фазообразовании, возможно, является причиной того, что, например, при электролитическом выделении новой фазы на постороннем электроде вычисленные размеры зародышей получаются порядка нескольких молекул или даже долей молекулы. Интересно отметить, что при этом в других отношениях эксперимент согласуется с макроскопической теорией.
Указанное, очевидно, относится и к выделению новой фазы на частично смачиваемых ядрах конденсации. Указание Гиббса в этом смысле [1, стр. 261 ] было реализовано Крыстановым [8], но, к сожалению, без учета линейного натяжения по периметру смачивания ядра каплей-зародышем.
Гиббс [1, стр. 296] допускает и возможность неравенства х < 0. Ниже мы приводим данные [10] для специального случая ньютоновской пленки; согласно последним в зависимости от концентрации электролита по периметру пленки значения х могут меняться от положительных к отрицательным. Поэтому целесообразно рассмотреть и влияние х < 0 на процесс гетерогенного образования новой фазы.
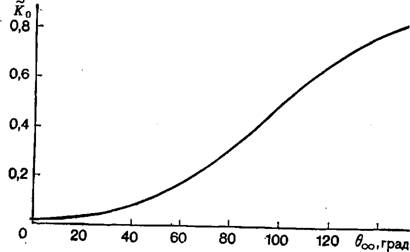
Вывод формул (76) и (9) для капли на плоской твердой подкладке допускает такую возможность. При этом оказывается, что согласно (76) с уменьшением г капли угол ее смачивания 0 также уменьшается. Однако, согласно (9), еще до того, как этот угол станет равным нулю, работа образования зародыша может стать нулевой. Это означает, что для х<0 при определенных пересыщениях, соответствующих согласно (1) определенным значениям Ко = 0ДЛЯ = 0, гетерогенному выделению новой фазы энергетический барьер не препятствует, а скорость выделения ограничивается только кинетическими обстоятельствами (переносом вещества на каплю). Мы подсчи-
Тали, используя (9) и (7в), эти значения Ко в зависимости от
|
Рис. 4. Теоретически вычисленная зависимость безразмерной кривизны К0 смачивающей капли, когда работа ее образования равна нулю, от угла смачивания бос большой капли. |
Угла смачивания ()«, большой капли. Как видно из рис. 4, эти значения много меньше единицы для малых в,*.
При х < 0 наши рассуждения относительно К0 не столь общи, поскольку в этом случае 0 < 0» и и’ < V, которые для малых углов и так очень малы. Мы подсчитали V‘/V по уравнению (14) с 0 для W2 = 0 в широком интервале значений 0» (от 20 до 150°) и установили, что V‘ меньше V всего примерно в два раза (0,49 для 0.» = 20° и 0,58 для 0„ = 150°).
|
(15) (6а) (16) |
|
DF — [2Лг (оа — ар) + 2ях] dr = 0 Ах = <*р — °а = к/’ D*F |
Если линейное натяжение отрицательно, равновесие двумерных фаз а и р (с поверхностными натяжениями сга и его), разделенных круглым контуром (рис. 5) устойчиво [1, стр. 296]. Действительно, тогда из экстремума свободной энергии Гельм — Га^ьца F при постоянной площади двумерной системы
|
= —2я х/г > 0 |
|
Дг2 |
Следует, что и
Равновесие линзообразной массы фазы С (см. выше) неустойчиво {1, стр. 261]. Учет линейного натяжения не сказывается На этом заключении, если х > 0. Для х < 0 с учетом полученного выше результата для двумерных фаз (16), возможен специальный случай, когда жидкое образование (на твердой под-
|
|
Р
Рис. 5. Равновесие двумерных фаз, разделенных круглым контуром.
Кладке, например) будет находиться в устойчивом равновесии с соседствующими фазами, т. е. не будет зародышем новой фазы. Действительно (см. рис. 2, б), из выражения
— ~ я (г* + h*) Р0 + 2лЛ(Т J dh + [—nrhP0 —F 2nra +
(авс ~ аАв) 2jlr + 2лн] Dr —0 (15a)
Следуют уравнения (3) и (7a), откуда, а также из соотношения
|
(16a) |
D*F d*F t d*F
DF =
Dhdr ) ^
Dh? Dr* Находим, что при
К > Sin3 6/cos 6
Капля на подкладке находится в устойчивом равновесии с соседними фазами. Этот случай не совпадает со случаем «безбарьерных» зародышей, получающихся при К0 (см. выше).
 3 января, 2013
3 января, 2013  admin
admin 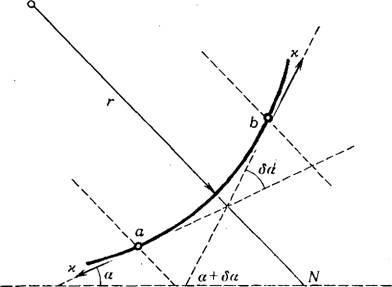

 Опубликовано в рубрике
Опубликовано в рубрике 