Лако-красочные материалы — производство

Исследование эффектов перекрытия в тонких прослойках жидкости или газа приводит к другим отличиям от гиббсовской системы термодинамики гетерогенных систем. Одно из принци­пиальных отличий выявляется для частного случая, когда про­слойка фазы 3 разделяет две тождественные фазы 1 и 2. Б этом случае возможен подход, когда вместо двух геометрических поверхностей раздела, локализация которых произвольна, рас­сматривается одна квазиповерхность раздела, расположенная точно в плоскости симметрии прослойки. Это позволяет исклю­чить всякую неопределенность при введении избытков масс компонентов, энергии и энтропии, отнесенных к этой плоскости и фактически характеризующих избыточное содержание этих экстенсивных величин в функции толщины прослойки. Так, если, например, концентрация I—Го компонента в фазах 1 и 2 есть Ct и объем системы V, то избыток i-ro компонента в про­слойке равен

Ат; — mi —

Где mL — общая масса t-ro компонента.

Предполагается, что объем системы определяется на основе положения поверхностей раздела с внешней фазой или со стен­ками сосуда, местонахождение которых соответствует нулевой адсорбции компонента I. Величина AMh таким образом, опреде­ляется независимо от толщины прослойки H, которая при ма­лых H точно неопределима. Конечно, при переходе к статисти­ческим методам необходимо использовать третье измерение и какой-то эквивалент толщины прослойки. Однако при этом вве­дение условных геометрических поверхностей раздела, выде­ляющих прослойку, не является решением проблемы.

При использовании единой поверхности раздела между двумя одинаковыми фазами удалось [6, 71 построить термодинамику симметричных пленок и найти условия равновесия и устойчи­вости равновесия для систем с тремя и четырьмя компонентами’ [8]. При этом вследствие эффекта перекрытия натяжение

1

1

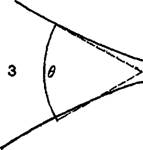
Рис. 3. Краевой угол на периметре свободной симметрич­ной пленки.

Такой пленки не равно удвоенному натяжению <т13 на границе фаз 1—3. Если оно меньше этой суммы (обычный случай), то возникает квазикраевой угол между объемной фазой 3 и ее про­слойкой (рис. 3).

Принципиальное отличие этого краевого угла, впервые рас­смотренного Мартыновым, Гутопом и мной 193, от обычного заключается в том, что самим своим существованием он обязан Эффекту перекрытия. В противоположном случае, когда натя­жение прослойки превышает удвоенное значение а13, отличного от нуля краевого угла не возникает. Тем не менее прослойка может находиться в равновесном сосуществовании с объемной фазой 3 при определенной толщине, что подробнее рассмотрено в [10]. Отметим, что условия устойчивости равновесия свобод­ных пленок в четырехкомпонентных системах, впервые рас­смотренные в [8], существенно сложнее, чем при меньшем числе компонентов.

Тогда, когда прослойка фазы 3 находится между двумя неодинаковыми флюидными фазами 1 и 2, краевые углы а и £ (рис. 4) можно определить из треугольника Неймана, одной из сторон которого служит натяжение прослойки. Тем не менее и этот случай не тривиален, ибо отличие углов а и (J от нуля также проистекает целиком из эффекта пере­крытия.

В этом случае нельзя определять избытки экстенсивных ве­личин, как в симметричном случае, не рассматривая толщину прослойки. Однако можно подойти к их определению иным спо­собом, имеющим общую применимость. Мы уже^рассматривали избыточную свободную энтальпию. Она равна^изменению сво­бодной энергии Гиббса системы, возникающему при образовании тонкой прослойки в результате эффекта перекрытия; ее можно

Рис. 4. Краевой угол на границе прослойки между неоди­наковыми фазами.

Оо

Вычислить по формуле AG = IS. Dh. Аналогично, измерив теп­

H

Лоту образования тонкой прослойки Л, можно найти ее избыточ­ную энтальпию и, следовательно, зная избыточную свободную энтальпию, — избыточную энергию.

По изменениям концентраций 1-го компонента в объемных фазах 1, 2 и 3 и их объемам и изменениям, вызванным образо­ванием тонкой прослойки, т. е. эффектом перекрытия, можно определить избыточное содержание 1-го компонента.

Все эти избытки должны определяться в функции толщины прослойки H. В этом — главные осложнения как для проведе­ния экспериментальной процедуры, так и с принципиальной точки зрения в связи с недостаточной определенностью понятия толщины для пленок, толщины которых приближаются к моле­кулярным размерам. Эта ситуация наиболее резко характери­зует отличие данного направления от направления классиче­ского труда Гиббса, хотя оно и является его естественным раз­витием. В то же время это развитие перекидывает мост от чисто термодинамической трактовки гетерогенных систем к трактовке, использующей для расчета поверхностных сил в гетерогенных и дисперсных системах статистические и молекулярно-физи — ческие методы.