По крайней мере для благоприятных ситуаций открытые бислойные мембраны можно реализовать при температурах выше Тс, следуя процедуре их формирования, предложенной Тагаки, Азума и Кишимото [14]. Такая бислойная система является открытой по отношению к (нерастворимой) липидной монослойной пленке, поддерживаемой при постоянных Т, р£, Р3 или Т, Yf, р3. В этом случае выражение для дифференциала свободной энергии имеет вид:
DF?i> = ~S? i) dT + У"1 dAm + Л + Из dn?(i) (33)
Компонент 2 поставляется без затруднений из монослойного резервуара, химический потенциал в котором равен р£. Уравнение (33) может быть проинтегрировано непосредственно, т. е. растяжение мембраны и формирование дополнительной мембранной поверхности неразличимы, коль скоро монослойный.
Резервуар достаточно велик. Результирующим интегральным соотношением, конечно, является
= + (34)
Что согласуется с уравнением (1) с той разницей, что уравнение (34) не является определением.
Комбинируя уравнения (33) и (34), как обычно, получаем:
—Dym = [SyAm] DT + + Г»(1)£/рз (35)
Это фундаментальное уравнение гиббсовского типа. Оно отличается от уравнения (13) для частично закрытой бислойной мембраны более своим применением, чем формой.
Экспериментально Yf предполагается независимой переменной вместо Переход от независимой переменной к Yf Легко осуществить подстановкой в уравнение (35) выражения
-dpj = Sf2 (1) dT + A[dyf + Y[ (1)dp3 (36)
Справедливого для монослойной пленки.
Таким образом, мы получаем фундаментальное уравнение
A? dym = — [S»(1) — Sf2 (1)] DT + 4 Dyf — [У»(1) — Yf (1)] dH (37)
Это уравнение, очевидно, содержит следующие частные производные:
^Х/, = — 4 (1) (38>
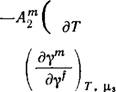
|
А? Г{ |
|
(40) |
2 2 (39)
Лт( дут _ Т _Yf
2 Ups )т. уГ~Г*М 3<»
Температурный коэффициент мембранного натяжения, определяемый по уравнению (38), следует ожидать положительным, так как предположительно S™(1) < SЈ(1) по той причине, что поверхностная энтропия в монослое связана с областью концов углеводородных цепей. Скорость изменения ут с Yf определяется величиной Ар. Когда рассматриваются относительно плотно — упакованные монослои, производная (дут/ду?)т, д3 должна быть приблизительно равна двум. Однако на основании измерений мембранного натяжения для обсуждаемых систем возможна, в принципе, точная оценка величины Ар. Следует ожидать, что частная производная (Дут/дц3)т, Yf мала, поскольку разность YpiX) — У£(1), вероятно, мала в большинстве’случаев.
 4 января, 2013
4 января, 2013  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике 