4 января, 2013 
admin Этот случай соответствует наиболее общепринятой процедуре приготовления бислойной мембраны [1], в которой используется подходящий органический растворитель (компонент 4) для липида. Ради простоты допустим, что липидный растворитель (компонент 4) является чистым. Предположим также, что фаза
|
Ламеллярный жидний нристалл
Рис. 6. Схематическая иллюстрация равновесного образования одиночного бислоя из ламеллярного стандартного состояния объемной фазы. |
Для того чтобы выделить бислой, натяжение ут должно быть сбалансировано внешней силой.
Растворителя содержит только компоненты 2 и 4 в ощутимых количествах, а компонент 3 присутствует только в воде. В соответствии с правилом фаз число степеней свободы равно трем. Таким образом, Т, р3 и р3 представляют удобный набор независимых переменных. Значение химического потенциала р2 определяется в фазе растворителя, а р3, как и ранее — его значением в водном растворе. Дифференциал свободной энергии для открытой бислойной мембраны такого типа равен:
DFfr = —S™ dT + Vm dAm + P2 dn™ + P3 Dn^{) + N dn™ (41)
Интегрируя, как обычно, это выражение при постоянных 7 р2 и р3 (а как следствие, и при постоянных Ymt р4) и сопоставляя затем с уравнением (41), получаем следующее фундаментальное уравнение
~Dym = [SyAm DT + Г»DH + + Т? йуц (42)
Имеющее вид уравнения Гиббса—Дюгема.
Сейчас очевидно, что di2 не является независимым дифференциалом, так как существует соотношение Гиббса—Дюгема для фазы растворителя (верхний индекс L), записываемое как
О = S%DT + + D^ (43)
Где = S4ni и Yt =
Вводя уравнение (43) в уравнение (42), получаем:
~dym = [(S^/Am — T? SL/Y{) dT + (Г— — Rf /Yi)d^ + Г™(I)
(44)
По своей внешней форме это уравнение близко к уравнению Гиббса для поверхностного натяжения. Следует отметить, в частности, что производная (дут1дк,^)т, ц3 не дает Гр, если только не сделано предположение, что избыток бислоя по органическому растворителю Tf очень мал при *** 1. Однако оказывается, что поверхностная плотность Г^, может быть определена на основании измерений ут при переменных концентрациях компонента 3 в воде, так как:
(дут/др3)7-> (Aj — ПГ(1) (45)
Примеры приложения уравнения (45) можно найти в литературе (см. [1]). Альтернативной формой уравнения (44) является
—Dym = [Sf}j/i4 — — I— DT +
+ [rf (diiJdX^)T + Tf (дН/дХ^)Т] dX + Г-(1) (дН{<Щ)т dX3 (46)
Где Ту XXf используются в качестве независимых переменных, a X. f и X® являются мольными долями соответствующих компонентов в фазах растворителя и воды; тильдой (~) помечены парциальные мольные величины.
В системе кислый додецилфосфат —холестерин—додекан — — 0,1 М NaCl [3] обнаружен положительный температурный коэффициент для ут. Согласно уравнению (46) это означает, что справедливо неравенство
S— /А < трЦ + Г3-(1)5- + rf (47)
Или, что то же самое:
S2F(L) < + + (48)
Это представляется правдоподобным при качественном сопо — • ставлении состояний липида в органическом растворителе и в бислое.
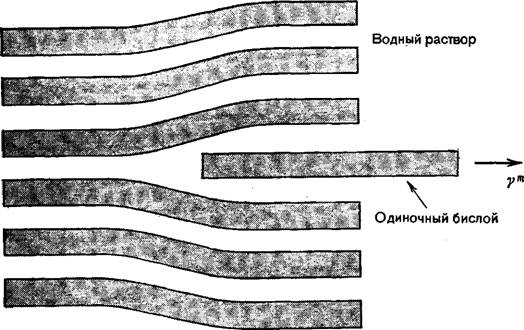
Опубликовано в рубрике 