На примере гетерогенного фазообразования мы показали как линейное натяжение влияет на этот процесс. Рассмотрим теперь образование новой поверхности без образования новой объемной фазы, когда линейное натяжение может играть определяющую роль.
Для объяснения роста кристаллов Странский и Каишев [9] предложили механизм зарождения нового монослоя на грани кристалла, работа образования которого xL/2 определяется свободной энергией х его периметра L.
На кривой, характеризующей сжатие нерастворимого монослоя на весах Лэнгмюра, часто наблюдается участок постоянного двумерного давления. Это указывает на переход от гомогенного газообразного состояния монослоя к гетерогенному состоянию с конденсированными участками. К сожалению, до сих пор не удалось выявить условия возникновения измеримого пересыщения при этом переходе, а также нет надежных способов контроля за числом возникающих пятен конденсации, хотя наличие таковых как экспериментально установленный факт и описано в литературе [11]. Рассматриваемое поэтому нельзя использовать для обнаружения и измерения линейного натяжения периметра пятна конденсата монослоя.
Новая граница раздела между двумя объемными фазами возникает всегда, когда флюидная фаза прижимается или сталкивается с другой флюидной или твердой фазой. Подобные контакты возникают: при взаимодействии капли или пузырька с твердой поверхностью (смачивание); при касании твердой частицы поверхности раздела двух флюидных фаз (при флотации, например); при встрече капелек двух несмешивающихся жидкостей в третьей. Кроме того, на границе раздела двух одинаковых жидких или газообразных фаз при определенных условиях может образоваться тонкая, в том числе и ньютоновская, черная пленка,, являющаяся новой двумерной фазой, ограниченной периметром смачивания. Если эта пленка не образуется или же прорывается, наступает коалесценция.
Все эти явления характеризуются дополнительной деформацией соединяющихся жидких фаз, за счет чего и возникает протяженный контакт между ними. Это соединение фаз отличается от соединения твердых тел, происходящего без такой самопроизвольной деформации. Упрочнение контактов между твердыми фазами за счет перекристаллизации и возникновения мостиков между ними соответствует деформационному укреплению контакта между жидкими фазами.
Возникновение контакта между жидкими или жидкой и твердой фазами сопряжено с некоторым энергетическим барьером, обусловленным действием линейного натяжения, если оно положительно. Рассмотрим в качестве примера соединение твердой сферы с жидкой границей раздела (жидкость—жидкость или жидкость—газ), который был положен в основу капиллярной теории флотации (рис. 6) [12].
Искривление плоской поверхности под влиянием прижимающей силы, характеризующееся углом у > О, образует капиллярную силу реакции
Fa = 2яг a sin у (17)
По которой измеряется поверхностное натяжение в весовых методах, в том числе и со сферой [13]. При достаточно больших г все натяжения по периметру смачивания компенсированы согласно (7) при —а, что и задает положение этого периметра на сфере. Если г, однако, очень мало, то условие (7) не может быть выполнено даже когда 9 = 0. В таком случае остается некомпенсированной некоторая доля ах, а именно:
TOC o "1-3" h z Ьо>с = ————— (18)
‘ ‘сг
Здесь гсг —критический радиус периметра смачивания, соответствующий последней возможности компенсации натяжений вдоль поверхности сферы при обращении 9 в нуль:
AAB — авс — aAC + х COS AJrcr = 0 < 19>
Это условие совместно с (8) и sin a = R/R дает для малых асп Т. е. когда cos acr ^ 1
Тсг = -—— (19а)
Сг 1 — Cos 0те 4 ‘
Где а = аАС.
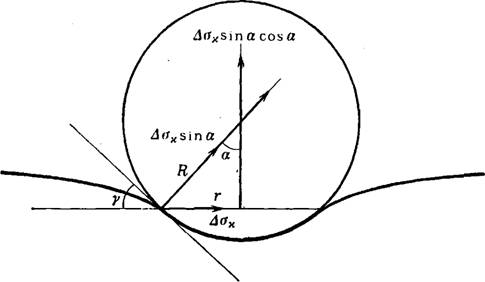
На рис. 7 некомпенсированная доля натяжения Аон (направленная для х > 0 к центру периметра смачивания) проектируется по нормали к сфере и полученное, перенесенное на центр сферы, проектируется по вертикали. Сила AaK sin a cos а на единицу длины периметра смачивания, умноженная на длину этого периметра 2яг, дает составляющую силы
Fi, = 2лги sin a cos a ( ————————— —^
X V r rcr /
Cr
= 2nx sin2 a cos a ( ————————— r^—^ (20)
Sin a sin Acr J
Которая вместе с Fa должна быть уравновешена внешней прижимающей силой G для того, чтобы сфера была в равновесии
G= 2nRo sin2a |"l + f-J————————————— r-^—— cosal (21)
L R sin a sin acr J J v ‘
Где г выражено через центральный угол a.
Для области малых G, при которых г < гсп согласно вышеизложенному, угол смачивания сферы жидкостью 9 равен нулю. Поэтому у в (17) равно а и Fa = 2tt#asin2a.
Выражение (21) можно записать для этого случая и в виде
G = 2яRat sin 2 a (22)
|
Рис. 6. Схема профиля твердой сферы, лежащей на нижней поверхности висящей капли. |
Где эффективное натяжение равно:
= it-ltakr)’08* <23>
Иными словами, система ведет себя так, как если бы натяжение жидкости было повышено на компоненту Асгх cos а.
Выражение (21) показывает, что при G = О, а = 0 и периметр смачивания плавно возрастает с G до г == гсг при
Gcr = 2NRcra sin2 acr = F0j cr (24)
Когда A а с ним и обращаются в нуль.
При G сколь угодно мало превышающем Gcr и г > гсг угол смачивания 9 получает возможность расти, а вместе с ним возрастает и г. Ситуация должна уже удовлетворять условиям
G = 2NRa sin a sin (а — 9) (25)
И
— (cos 0 — cos 0те) tga (26)
Согласно выражениям: (17) с у = a —0; (7) с г|) =я — а; (8) и стАс = а—
Таким образом, для G = GCr имеется два решения, одно для 0 = 0 и г = = гсп а второе для 9 > 0 и г = г2- Для достаточно больших R периметр смачивания настолько возрастает, что 9 становится почти равным 9,*, так как член с »е становится исчезающе малым.
|
Рис. 7. Схема, иллюстрирующая взаимосвязь некомпенсированной части и прижимающей силы. |
Кроме того, при переходе G = GCr от rt к г2 » гх угол у2 = = а — 0 сильно сокращается по сравнению с ух = уСп так как Gcr = 2лг! сг sin2 Yi == 2лг2а sin2 Y2, и в большинстве случаев, даже для G > Gcr можно полагать у О, т. е. а « 0, так что г2 можно оценивать по приближенной формуле г2 = Rcr sin О*,.
Проиллюстрируем вышеизложенное на конкретном примере малой твердой сферы, которая прижимается своим весом изнутри висящей капли к ее нижней поверхности. Пусть для простоты капля велика и ее поверхность можно считать плоской.
Прижимающую силу, равную весу сферы в жидкости, запишем в виде
G = — j — nR3pg (27)
Где G — ускорение свободного падения;
Р — разность плотности сферы и жидкости.
Выражение (27) не совсем точно, так как в нем не учитывается измененный вес выступающей из жидкости части. Однако Шелудко и Николов [13] на основе точных расчетов показали, что для достаточно малых сфер и малых углов смачивания формула (27) точна.
Положим: х’= 10"5 дин; а = 50 дин/см, pg = 10s дин/см3 и О,» = 20°. Поскольку мы выбрали материал сферы и жидкости так, чтобы большая сфера образовывала значительные угол смачивания 0» = 20° и оголенную, непокрытую жидкой пленкой поверхность, то малая сфера так же непременно образует
|
|
|
Г, мкм 5 |
|
4 |
|
2 |
|
0 2 4 —8’1"’ 10 12 14 R, mhm |
|
Рис. 8. Зависимость периметра смачивания г от радиуса твердой сферы, находящейся в равновесии на жидкой поверхности раздела, вычисленная для 9«, = 20°, х = Ю-5 дин, а = 50 дин-см-1 и Pg = 103 дин* см-3. |
|
3 |
|
Г, МММ T),05 |
Истинный (без пленки) контакт. Действительно, пленка, первоначально покрывающая выступающую поверхность сферы, находится под значительно повышенным давлением 2A/R, Которое ее прорывает, раз и без этого давления (большая сфера) пленка неустойчива.
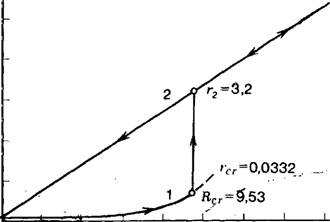
Выразив G через R, мы можем рассчитать согласно (21) участок зависимости г = F (R) для 0 < г < гСт, показанный на рис. 8 (кривая 1) при растянутом масштабе для г (нанесенный справа). Конечная точка этой кривой имеет координаты гСг — = 3,32- 1(Гв см и RCr = 9,53- 10"4 см.
При R > RCr угол 9 становится положительным и оба угла 9 и а начинают расти самопроизвольно до тех пор, пока не будет удовлетворена система уравнений (25) и (26), решение которой дает второе значение г = г2 при R = Rcr, а именно 3,2-10"4 см. Таким образом, при переходе через R = RCr должно наблюдаться стократное возрастание периметра смачивания. И если до этого г было ненаблюдаемо мало, то после этого перехода радиус периметра смачивания становится соизмеримым с ^ и микроскопически наблюдаемым. Это, конечно, зависит от угла 9», с которым угол 9 после рассмотренного перехода почти становится равным.
Для кривой 2 (рис. 8), на которую мы перешли, а « 9, что очень близко к 9,» для R, равных и даже больших, чем RCr. При уменьшении R по кривой 2 мы возвращаемся к R — 0 при г — 0. При этом 9 убывает по сравнению с 9». На рис. 9 (кривая
|
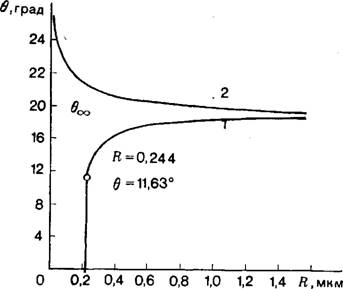
Рис. 9. Зависимость угла смачивания 0 малой твердой сферы, находящейся в равновесии на жидкой поверхности раздела, от ее радиуса, вычисленная для 0те = 20°, х = = Ю-5 дин, а = 50 дин-см-1 и Pg = 103 дин-см-3. |
1) показан участок зависимости 0 = F (R) для очень малых и убывающих R. Как видно, 0 понижается до 0 = 0m = 11,6° при R = Rm = 2,44- Ю-5 см, после чего скачком переходит в нулевое значение, и мы снова оказываемся на кривой 1 рис. 8. При этом г еще не равно нулю и продолжает понижаться согласно уравнению (21). Этот участок не заметен на рис. 8 из-за грубости масштаба по R. Скачкообразный переход 0 при 0т в нуль, когда R становится равным Rm, соответствует обращению в нуль производной DR/DQ от описывающей кривую 1 (рис. 8) зависимости (N/O)/R = (cos 0—cos 0,») tg 0 [формула (21), в которой а положено равным 0]. Условию DR/DQ =0 соответствует равенство:
Cose^tcose^)1/* (28)
В случае х < 0 угол 0, наоборот, возрастает, причем плавно от 0=0» при больших R, стремясь к 0 = 90°, когда R стремится к нулю (рис. 9, кривая 2 длях=—10"5 дин). С увеличением R радиус периметра смачивания г плавно повышается без скачка по кривой, описываемой уравнениями (25)—(27).
ИЗМЕРЕНИЕ ЛИНЕЙНОГО НАТЯЖЕНИЯ — МЕТОД УМЕНЬШАЮЩЕГОСЯ ПУЗЫРЬКА. МЕТОД КРИТИЧЕСКОГО ПУЗЫРЬКА
Первая попытка измерить линейное натяжение была недавно предпринята Торца и Мезоном [14]. В специально приготовленной эмульсии фотографируются слипшиеся микроскопические капельки жидкостей А и В, взвешенные в жидкости С.
Натяжения оАС и авс известны, а натяжение между каплями аАВ определяется из кривизны трех поверхностей и известных двух натяжений по фотографиям двойных капелек. Далее, из формы этих капелек определяют углы у периметра контакта между ними. По отличию этих углов от углов, которые бы возникли при большем периметре контакта, когда ах = О, и эти углы определяются только значениями трех поверхностных натяжений, вычисляется линейное натяжение для контакта А, В и С.
В работе использованы пять фотографий двойных капелек. Вычисленные значения оя сильно отличаются друг от друга. Соответственно и значения х также рассеяны более чем на порядок, а в одном случае х получилось даже отрицательным. Таким образом, не было надежно определено ни значение х, ни его знак.
Причина этого неуспеха, нам кажется, кроется в том, что ось симметрии двойных капелек на фотографиях не была параллельна плоскости фотографии, как предполагается при расчетах. Такая дезориентация свободно плавающих двойных капелек по отношению к расчетной ориентации должна привести к кажущейся деформации поверхности контакта между капельками и к ошибочным значениям аАВ. Вычисленные значения х, кроме того, определены неверно из-за ошибочно определенных кривизны поверхностей и радиуса контакта, а также и углов у его периметра. Если бы авторы этой работы отдельно измерили аАВ и выбрали бы из всех фотографий двойных капель те, кривизна поверхности АВ которых соответствовала бы измеренным значениям <тАВ, то ошибки от дезориентации капелек были бы, вероятно, исключены.
Вторая попытка измерить линейное натяжение была предпринята в связи с капиллярной теорией флотации [13]. В этом случае была использована вторая возможность, отмеченная, в предыдущем разделе. Микроскопические стеклянные сферы (так называемые балотини), обработанные предварительно в подходящем растворе ПАВ так, чтобы угол смачивания для них был равен примерно 9«> = 20°, свободно оседали на нижнюю поверхность висячей капли из этого же раствора. Сферы раз
ного диаметра вели себя по-разному: более крупные образовывали хорошо заметные периметры смачивания при наблюдении в отраженном свете микроскопом снизу, а более мелкие покоились на жидкой поверхности без образования видимого периметра смачивания. Отсюда определялся радиус наименьших частиц, образующих видимый периметр смачивания, т. е. RCr, А с ним вычислялось линейное натяжение х по формуле
(29)
Которая следует из уравнений (19), (27) и (24) при г = R sin а.
Хотя полученное значение х « 10"5 дин и хорошо согласовывалось со средним значением х, вычисленным из флотационных данных в предположении, что нижний предел флотируе — мости соответствует размерам частиц порядка микрона и определяется работой образования двумерного зародыша контакта, этот результат также нельзя считать бесспорным.
Как справедливо отметил один из рецензентов этой работы, не исключено, что использованные стеклянные сферы были двух сортов: меньшие —с меньшим углом смачивания и большие — с большим, так что незакрепление малых частиц определялось не линейным натяжением, а их повышенной смачиваемостью. Проверить такое толкование было невозможно, так как угол контакта можно было измерить только для больших частиц, образующих видимый трехфазный контакт.
Надежные результаты по измерению линейного натяжения были недавно получены в работах [10]. Исследовался периметр ньютоновской пленки, полученной на выступающей части пузырька, всплывавшего на поверхность раствора лаурилсуль — фата натрия (NaLS) + NaCl в воде.
|
|
Использованные в этих работах очень маленькие пузырьки с радиусом Rb меньше 100 мкм имели сферическую форму, так как капиллярное давление в них на три-четыре порядка выше гидростатического. Поэтому пузырьки должны себя вести подобно твердым сферам, рассмотренным в предыдущем разделе. Отличие состоит в том, что контактная область в этом случае образована ньютоновской пленкой с радиусом кривизны Rf, Которая разделяет две одинаковые фазы. Натяжение пленки Д всего примерно на один процент меньше удвоенного натяжения обеих поверхностей, встречающихся у периметра пленки [14]. Так как капиллярное давление в пузырьке Ра = 2O/Rb = — 2&/Rf, то Rf почти точно вдвое больше Rb. Симметричность системы — равные натяжения больших фаз — обуславливает то, что касательная к пленке делит угол, заключенный между поверхностями жидкости и пузырька, точно пополам. Эту
половину принято называть углом контакта пленка — «большая» жидкость. На очень малых пузырьках (и пленках) появляется измеримое слагаемое ак. Хотя ак действует не вдоль пленки, а вдоль ее периметра, т. е. заключает некоторый угол касательной к пленке у ее периметра, симметрия системы почти не нарушается, так как ах остается и для самых малых исследованных пузырьков много меньше а. Все эти соображения, как это показано в [10, первая ссылка], ведут к следующей достаточно точной формуле для тангенциального равновесия
ХF = 4ORb (cos Qf — cos 0^) sin Qf (30)
Вместо (26) для твердой сферы.
Здесь центральный угол а =20F Г = Rb sin 20f, а
А = 2а Cos 0^ (31)
Выражение (30) ведет к примерно такой же зависимости угла Of От Rb, как и для твердой сферы (рис. 9).
При всплывании очень малых пузырьков образование ньютоновской пленки (как и образование оголенной поверхности на твердой сфере) ограничено действием линейного натяжения (если оно положительно). И только тогда, когда сила G =
=Jt-ftDpg (27), прижимающая пузырек, больше некоторого
Критического значения Gcn образуется видимая ньютоновская пленка.
Согласно условию (19), где аАВ = Д и авс = адз = а, и совместно с (31) и для 0^=0 получаем вместо (19а) выражение:
Гсг=х’/2а( 1-cosfl^) (32)
Далее, поскольку при G = Gcr, Fx = 0 и Fa = 2NRcra Х X Sin2 Асп где Sin acr = rcr/Rb, Получаем для Fa = GCr
У! = 2 У Pga (1 — cos ©У R2Cr (33)
Вместо (29) для твердой сферы.
Формулы (30) и (33) позволяют измерить линейное натяжение по изменению угла контакта ньютоновской пленки на уменьшающемся пузырьке [согласно (30)] и по наименьшему (критическому) пузырьку (Rb =Rcr), который при всплывании образует видимую ньютоновскую пленку [согласно (33)].
Выбранная в [10 ] система очень подробно изучена в работах [15, 16], так что Д, а и 0да известны надежно. Параметры пленки-контакта, в отличие от контакта на твердой сфере,
|
|
14 * V
|
12 — |
|
|
|
|
|
10 |
|
3 2 |
|
8 |
/
6 I
4
2
____ I___ I___ ‘ i ‘ ‘ I I i I
О 10 20 30 40 50 60 70 80 90Яй, мкм
Рис. 10. Зависимость угла контакта 0^ ньютоновская пленка — большая жидкость от радиуса Rb всплывающего пузырька: концентрации NaCl, М:
1 — 0,320; 2 — 0,360 и 3 — 0,450 [10, вторая ссылка].
Воспроизводятся очень хорошо. Пузырек, газ в котором сжат дополнительно капиллярным давлением за счет диффузии этого газа из пузырька, самопроизвольно уменьшается. Это делает особенно удобными измерения по формуле (30). Все измерения по обоим методам были проведены с одной и той же концентрацией NaLS (0,05%) и разными концентрациями NaCl при
25 °С.
Относительно большой пузырек (Rb > Rcr), всплывший на поверхности раствора, можно подходящим образом наблюдать (см. [10, вторая ссылка]) в процессе его уменьшения. В результате получается набор значений Rb и г, которые при пересчете по формуле sin 20^ = R/Rb дают & = / (Rb). Эти данные, согласно (30), позволяют определить к и OL. Совпадение последнего для каждого раствора NaLS +.NaCl с наиболее новыми данными де Фейтера [16] подтверждает правомерность применения формулы (30).
|
Ч |
Несмотря на отличную воспроизводимость параметров системы, значения 9f — [ (Rb) значительно рассеяны, главным образом из-за Небольшой точности измерения Rb и в особенности г. Поэтому для каждой концентрации проводилось измерение с несколькими пузырьками и полученные значения (порядка сотни) обрабатывались статистически, как это подробно описано в [10, вторая ссылка].
Усредненные результаты этих измерений приведены на рис. 10 для трех концентраций NaCl. Как видно, при концентрации NaCl 0,320 моль/л (кривая 1) угол Qf уменьшается с уменьшением Rb, что соответствует х^ = 7,6- Ю-5 дин; при концентрации 0,360 (кривая 2), Qf почти не меняется, т. е. х^ » 0; и, наконец, при концентрации 0,450 (кривая 3) Qf возрастает, т. е. натяжение периметра пленки отрицательно (х^ = —12,9 X X 10~б дин).
Стрелками показаны соответствующие значения 9», очень хорошо совпадающие со значениями, измеренными в [16] другим методом для тех же растворов. На рис. 10 части кривых, подтвержденные экспериментом, обозначены сплошными линиями, а не подтвержденные —даны пунктиром. Нижний предел по Rb использованных пузырьков определялся тем, что очень малые пузырьки исчезают почти мгновенно за счет диффузии под высоким капиллярным давлением в них. Интересно, что удалось подойти вплотную по кривой 1 до точки перегиба, предсказанной для случая с твердой сферой при х > 0. Значение 9т, соответствующее DQf/DRb — оо, получается из (30) в виде формулы (12) ей» = 9^, вместо (28) для твердой сферы.
Второй метод — метод критического пузырька — был применен [10, первая ссылка] для измерения xf при концентрациях NaCl меньше 0,360 моль/л (х’ > 0). Очевидно, что для х^ < 0 всегда должна образовываться видимая ньютоновская пленка; это и наблюдалось для больших концентраций NaCl, так что в этой области метод критического пузырька неприменим.
Специальным приспособлением, описанным в [10, первая ссылка], выдавливанием и электролизом получали под поверхностью раствора пузырьки водорода разной величины, в том числе и очень малые. Начиная с некоторого размера, они образовывали на своей выступающей (после всплывания) поверхности ньютоновские пленки. Это явление очень четко наблюдалось в виде мгновенного расширения на пузырьке черного пятна и исчезновения ньютоновских колец интерференции, которые до того (или на меньших пузырьках) обрамляли центральную темную часть купола пузырька. Частота образования видимых ньютоновских пленок возрастала с ростом Rb над RCr, И на достаточно больших пузырьках всегда возникали видимые пленки. Учитывая, согласно соображениям, изложенным во втором разделе, что при Rb^.Rcr состояние с субмикроскопическим контактом устойчиво, /^определяли по начальному участку кривой: частота появления пленки —размер пузырька. Из найденных так экстраполяцией значений Rcr по зависимости вероятности
|
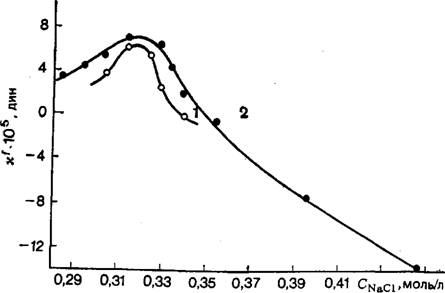
Рис. 11. Зависимости линейного натяжения х ньютоновской пленки от концентрации NaCl, полученные методом критического пузырька (/) [10, первая ссылка] и методом уменьшающегося пузырька (2) [10, вторая ссылка]. |
От Rb, т. е. снова статистически, для каждой концентрации NaCl вычисляли согласно (33) кК
Все полученные значения в зависимости от концентрации NaCl показаны на рис. 11, где кривая 2 относится к методу уменьшающегося пузырька [10, вторая ссылка], а кривая 1 — к методу критического пузырька [10, первая ссылка]. Как видно, область для nf > 0, определенная обоими методами, дает близкие значения для уО — F (CNaci). Так как в обоих случаях значение vJ получено путем статистической обработки большого числа отдельных измерений, вряд ли можно приписать систематически более низкие значения xf, полученные методом критического пузырька, невысокой точности измерений Rb а г для первого метода и Rb = Rcr для второго. Скорее всего, дело в том, что условия эксперимента в обоих случаях по-разному отличались от модели, при помощи которой их интерпретировали. В последней принято, что натяжение пузырька равно натяжению плоской поверхности жидкости. Между тем свежеобразованный пузырек, сразу всплывший к поверхности (метод критического пузырька), в момент соединения с поверхностью раствора вряд ли успевает путем адсорбции понизить натяжение •до равновесного значения натяжения плоской поверхности. Наоборот, в методе уменьшающегося пузырька, когда его размеры сильно сократились до размеров, где 9^ начинает заметно изменяться по сравнению с 9„, и когда скорость уменыие — ния поверхности значительна, возможно, что плотность адсорб-. ционного слоя на пузырьке выше равновесной, а натяжение, соответственно, ниже. Если эти соображения в дальнейшем подтвердятся, то правильные значения nf должны лежать между обеими кривыми, т. е. точность определения xf составляет ~10~б дин.
Порядок полученных значений линейного натяжения, равно как и то, что оно меняет свой знак под влиянием повышения концентрации электролита, не вызывают сомнений. Последнее противоречит теоретическому выводу де Фейтера и Врея [17], что пленки всегда должны иметь отрицательное линейное натяжение по линии перехода к большой жидкости.
ЗАКЛЮЧЕНИЕ
Возвращаясь к исходной проблеме этого обзора — к проблеме малой фазы, можно сделать следующее замечание. С позиций формальной термодинамики рекомендованное Гиббсом введение линейного натяжения (и соответствующих избытков) [1, стр. 288] решает вопрос описания систем с трехфазным контактом для тех случаев, когда размеры фаз достаточно велики. При молекулярно-статистической трактовке этого случая, однако, положение значительно сложнее, чем в случае двух фаз. Например, для капли в парах без особой потери точности можно применять параметры больших фаз (например, поверхностное натяжение), рассчитывая их только с учетом ближайших соседей. В случае линейного натяжения в наиболее важных случаях относительно больших углов контакта 9«, в области, где встречаются три поверхности без пленки заметной толщины (или ньютоновской пленки) расстояния между поверхностями доходят до молекулярных. При этом учет взаимодействия молекул всех трех фаз в этой зоне становится обязательным. Таким образом, эффекты типа расклинивающего давления в тонком слое выступают здесь со всей силой. Однако простое сведение проблемы к проблеме тонкого слоя вряд ли допустимо, так как расстояния между поверхностями всех трех фаз в зоне контакта между ними одного порядка.
Описанные выше методы измерения линейного натяжения по своему характеру универсальны, и в настоящее время начаты опыты по их применению к другим системам: капля или пузырек и твердая поверхность, или граница раздела двух разных флюидов.
Можно надеяться, что подобные исследования позволят шире применить линейное натяжение при описании поведения микрогетерогенных дисперсных систем и приблизят нас к более полной молекулярной интерпретации этого параметра.
 3 января, 2013
3 января, 2013  admin
admin 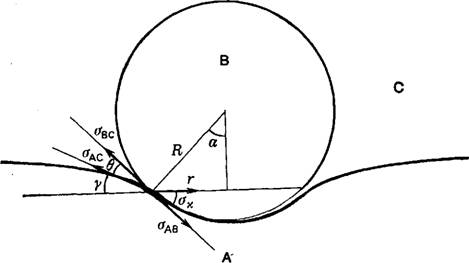
 Опубликовано в рубрике
Опубликовано в рубрике 