Очень мелкие частицы движутся вместе с жидкостью. Их траектории совпадают с линиями тока жидкости, т. е. искривляются вблизи пузырька. Крупные частицы обладают большой инерцией и движутся почти по прямой, приближаясь к пузырьку. Чем меньше частицы, тем меньше силы инерции. Существует критический размер частицы асг. При а < асг захват частицы за счет инерционных сил невозможен [26].
Флотация мелких частиц возможна либо за счет того, что по достижении определенного критического значения Hcr Утоньшающаяся при сближении частицы и пузырька пленка становится неустойчивой и разрушается, либо за счет дально — действующих сил притяжения, эффективный радиус действия которых в условиях флотационного акта также можно характеризовать введением параметра Hcr.
Теория гидродинамической стадии флотации мелких частиц Дерягина, Духина, Рулева [27, 28] до сих пор не учитывала
|
|
|
Дни |
|
|
|
ТЧаЛ) |
|
|
|
Tf[o, tM
|
А г
Рис. 1. Схема, поясняющая механизм эффекта стабилизации межфазной пленки динамическим адсорбционным слоем:
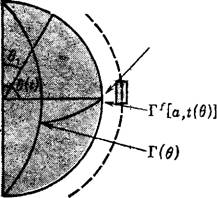
А — траектория пластинчатой частицы вдоль поверхности пузырька (0, —угол, характеризующий вхождение частицы в диффузионный слой пузырька в момент t — 0; В (<) — угол, характеризующий положение частицы в момент t; Г (0)— распределение адсорбции на поверхности пузырька; Г’ СО, / (0)], Г^ Ей, <(9)1 — временная зависимость адсорбции в центре и на периферии межфазной пленки;
Б — Г^ (0, T) н Г^ (A, T) — значения адсорбцнн в центре и на периферии межфазной пленки;
![]()
|
_________________________________ j |
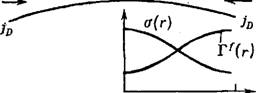
В — распределения адсорбции Г^ (Г) и поверхностного натяжения а (г) вдоль межфазной пленки в зависимости от расстояния г до ее центра (/£> — вектор диффузионного потока ПАВ): Г — распределение скорости вдоль поверхности пузырька, характеризующее втекание жидкости в межфазную пленку.
Влияния динамического адсорбционного слоя пузырька. Изменение адсорбции по поверхности пузырька приводит к тому, что в межфазной пленке адсорбция изменяется (рис. 1, а и б). Можно показать, что в центре межфазной пленки адсорбция Tf (О, /) меньше, чем на ее периферии Г^ (A, T), так что поверхностное натяжение в центре больше, чем на периферии пленки
(рис. 1,в). Но нарастание поверхностного натяжения от периферии пленки к ее центру должно сопровождаться поверхностным течением от периферии к центру (рис. 1, г), в которое вовлекается вся жидкость пленки. Втекание жидкости в зазор между частицей и пузырьком препятствует утоньшению пленки и исключает возможность флотации. Этот эффект естественно именовать стабилизацией межфазной пленки в элементарном акте флотации динамическим адсорбционным слоем. Этот, впервые замеченный, аналог эффекта Марангони—Гиббса, в элементарном акте флотации не возникает, если поверхность пузырька неподвижна. Покажем, что адсорбция в центре пленки
Г’|г = о = Го,; меньше, чем на периферии (А, T).
Пусть траектория частицы пересекает диффузионный слой при 0 = 0!, причем размер частицы больше или порядка толщины диффузионного слоя. Тогда в зазоре между частицей и пузырьком в момент погружения T — О частицы в диффузионный слой значение адсорбции поверхностно-активного вещества П (0, /) = Г (0Х). Перемещаясь вдоль поверхности пузырька, частица попадает в область иных значений адсорбции на поверхности пузырька, т. е. адсорбция поверхностно-активного вещества на периферии пленки непрерывно изменяется. Естественно отождествить адсорбцию поверхностно-активного вещества на периферии пленки с адсорбцией его в месте нахождения частицы, т. е. на той же параллели, на которой находится частица, но на некотором удалении от нее. Если координата центра частицы в момент T равна 0, то:
Г'(а, О-Г [9(0] (75)
Так как частица перемещается вдоль поверхности вместе с межфазной пленкой, можно было бы думать, что в центре межфазной пленки сохраняется первоначальное значение адсорбции, т. е.:
Г’ (0, 0 = г’ (0, 0) = Г (9Х) (76)
Сравнение формул (75) и (76) приводит к выводу, что в центре пленки адсорбция ниже (поверхностное натяжение выше), чем на ее периферии:
Г’ (а, 0 = Г [9 (01 > Г (0!> = Г’ (0, 0 (77)
Диффузия поверхностно-активного вещества от периферии пленки повышает значение адсорбции в центре, которая при этом остается неизбежно ниже, чем адсорбция в тот же момент на периферии [Г’ (0, T) < Tf (A, T)J. Расчет разности 6Г^ (г, T) = = Г’ (г, t) — Г’ (a, t), являющейся движущей силой процесса стабилизации межфазной пленки, удалось провести для случая пластинчатой частицы дискообразной формы, поскольку в этом случае пленку можно рассматривать как плоскопараллельную, а протекающие в ней процессы — как обладающие осевой симметрией, так что уравнение нестационарной диффузии принимает вид
DTf /d2Tf i Зтf
= 5+ — M
Где Ds — коэффициент поверхностной диффузии молекул по — верхностно-активного вещества.
Решение, удовлетворяющее граничным и начальным условиям
(О, О = 0; г’ (а, 0 = Г (0; г’ (г, в) = Г (Qj) (79)
Можно получить с помощью интеграла Дюамеля:
Мл С
In (0 = I [Г (т) — Г (0г)] е D +Г(0-Г(в1) (81)
D о
Здесь J0 и Jx —функции Бесселя первого рода; in — корни;
XD = a2/Ds — характерное время диффузии по пленке.
Преодоление стабилизирующего действия неравновесного адсорбционного слоя возможно за счет действия прижимной силы с нормальной составляющей поля скоростей жидкости, обтекающей пузырек. Близ верхней полусферы жидкость движется (постепенно замедляясь) к поверхности пузырька, обтекая частицу и тем самым прижимая ее к пузырьку. Сила, с которой поток прижимает дискообразную частицу с толщиной b к поверхности пузырька при Re 1 описывается формулой [29, стр. 174]:
Fx = 48т] ^ cos 9 (82)
А
Поток, прижимающий частицу к поверхности пузырька, порождает избыточное давление в межфазной пленке Bp (г), Которое должно уравновешивать прижимную силу:
А
F2 = | 2Nrbp (г) dr (83)
О
Существует предельное значение толщины пленки /гит» характерное в том отношении, что при H > HIm пленка утонь — шается под действием прижимной силы, а по достижении h = h[im толщина пленки стабилизируется, так как истечение жидкости из зазора под влиянием перепада давления компенсируется втеканием за счет перепада поверхностного натяжения. Предельную толщину пленки удалось рассчитать для случая плоскопараллельного зазора между дискообразной частицей и почти плоским участком поверхности большого пузырька. Она определяется из условия неизменности толщины пленки, которому соответствует равенство нулю потока жидкости через любое цилиндрическое сечение пленки
Hlim
J и (г, z) dz = 0 (84)
Где распределение радиальной тангенциальной скорости И (г, г) определяется совместным действием градиентов давления и поверхностного натяжения.
Влияние др/дг на и (г, Z) отражено в уравнении Навье— Стокса; влияние до/др учитывается при его решении в граничном условии, так как на поверхности, граничащей с воздухом, Dafdr должно быть уравновешено вязким напряжением в жидкости. Упрощение уравнения Навье—Стокса в рамках приближенного метода гидродинамики тонких пленок облегчило нахождение вида функции и (г, Z):
2=0 or
Здесь Z = 0 и Z — H соответствуют поверхностям межфазной пленки на границе с воздухом и твердой частицей.
Две неизвестные постоянные, появляющиеся при решении уравнения (85), определяются с помощью граничных условий (86). Подставляя полученные таким образом выражения и (г, Z) В (84) и интегрируя, получим связь между распределениями давления и адсорбции в межфазной пленке:
= (87)
Ит ог
Из этого уравнения можно получить формулу для И, цт, так как распределение адсорбции известно и выражается формулой (80), а распределение давления связано формулой (83) с прижимной силой
3 г
-Fx = пи—————- | 2nr6Т (г) dr (88)
О
Выражая левую часть уравнения (88) с помощью формулы (82) и известной формулы для скорости всплывания пузырька
U=~~gaVv (89)
(g — ускорение силы тяжести; v — кинематическая вязкость воды) и подставляя распределение адсорбции в правую часть этой формулы, а также интегрируя
А
TOC o "1-3" h z J У„ (М) ^ ((1„> (90,
0
Выразим /ijjm на основе получившегося соотношения:
Оо
И (Й- У 3nR а V РХя (О /он
ЛИт (0) — —W~B~ 2j (91)
П= 1
Здесь у выражается формулой (21).
Неявная зависимость 6 (/), характеризующая перемещение
Межфазной пленки вместе с частицей вдоль поверхности пузырька
Tg (92)
Получается при интегрировании уравнения движения элемента поверхности пузырька
R = у0 sin G (93)
Причем Xb = R/V0 — характерное время движения поверхности пузырька.
Аппроксимируя угловую зависимость адсорбции на верхней половине пузырька формулой
Г (6) = Г0 — ДГ Cos 6 (94)
Где
и используя также формулу (91) и проведя интегрирование, можно привести формулу (81) к виду:
8, ( -2t/xh ~v2nthD i Tn (0 = 2ДГ Tg2 e /b-e — ) (96)
На основе алгебраических преобразований, использующих формулы (95), (93) и (76), формула (91) может быть приведена к виду:
|
"и — а 2 |
L tg (6/2)1_________________ (97)
Эта формула существенно упрощается, если рассматривать 6 > 20i, что позволяет опустить сложный член, зависящий от 0j. Проведены расчеты зависимости кцт (0) при 0>20i и ряда значений Xbl2XD при 7/14 =0,3; а/Ь = 3 и R =0,1 см.
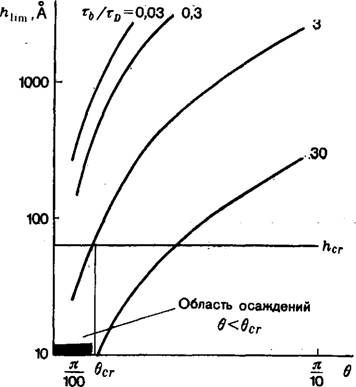
Приведенные на рис. 2 кривые рассчитаны для различных значений Tb/iD, что соответствует радиусам частиц 1, 3,3 и 10 мк, если считать, что Ds = Ю-5 см2/с2; хь =3 — Ю-3 с, V0 =
= V = 30 см/с при R = 0,1 см. Только в малой окрестности
Верхнего полюса пузырька частица может приблизиться к пузырьку на расстояние, меньшее hcn что необходимо для флотации. Область углов, определяемая из условия
Allm (Qcr) = К (98)
Столь узка (рис. 2), что эффективность захвата при условии стабилизирующего действия межфазной пленки совершенно ничтожна. Формула для 0СГ легко получается из (97), если произвести замены:
Йо + Liv** Г <99>
|
Y 9nR а „ 8 1 |
Время существования межфазной пленки (время движения частицы вместе с прилежащим участком поверхности пузырька) порядка тй; время выравнивания концентрации в межфазной пленке за счет диффузии порядка xD. Если xDl%b ^ 1, диффузионный процесс в межфазной пленке не успевает развиться в такой степени, чтобы повлиять на перепад концентрации. Поэтому при больших значениях этого отношения его влияние на эффект стабилизации, как это видно из формулы (99), мало.
|
Рис. 2. Предельная толщина межфазной пленки HUm для различных участков поверхности пузырька, характеризующихся углом 0. Область, для которой невозможность осаждения не доказана, |
При малых значениях этого отношения перепад поверхностного натяжения в межфазной пленке убывает за счет диффузионного выравнивания концентрации. Поэтому предельная толщина стабилизированной пленки оказывается тем меньше, чем меньше это отношение, как это следует из формулы (99).
Как видно из формулы (93) при 0 —> 0, скорость перемещения и, соответственно, частицы с межфазной пленкой неограниченно убывают..Поэтому, чем ближе частица к верхнему полюсу пузырька, тем в большей степени успевает выравниваться перепад концентрации в межфазной пленке. Поэтому кцт убывает с 0, как это видно из формулы (97), и осаждение оказывается возможным в окрестности верхнего полюса.
При переходе от пластинчатой частицы к сферической следует ожидать резкого ослабления эффекта стабилизации межфаЗной пленки. При этом же избыточном давлении в зазоре, вызванном прижимной силой, утоньшение пленки будет протекать более интенсивно, так как в случае сферы толщина межфазной пленки быстро возрастает с удалением от ее центра, что облегчает истечение жидкости. Будем считать, что, как и в случае с дискообразной частицей, вместе со сферической частицей радиуса а перемещается вдоль поверхности пузырька межфазная пленка радиуса а, т. е. граничные условия (79) сохраняют свое значение. Казалось бы, уравнение (78) в случае сферической частицы необходимо уточнить, так как толщина пленки по мере удаления от ее центра возрастает. Однако, если Ds ~ D и выполняется условие
Г/с > а (100)
То обмен между центром межфазной пленки и ее периферией идет преимущественно за счет поверхностной диффузии. В этом случае можно использовать уравнение (78) и, соответственно, его решение (80). Если одновременно выполняются условия (100) и (42), т. е. если
А< б (101)
Можно использовать и формулу (76).
Радиальное течение в зазоре между плоскостью и сферой можно приближенно рассматривать как плоскопараллельное — вблизи от центра пленки. Это упрощение становится все менее точным по мере приближения к периферии пленки. На периферии пленки возрастает и ошибка в описании распределения адсорбции, так как отождествление Tf [/, (0) ] с Г (0) при г = а весьма условно. Поэтому в качестве весьма грубого приближения рассмотрим радиальное течение в пленке как плоскопараллельное, т. е. воспользуемся уравнением (85) и граничными условиями (86), заменив H на H + гг/а. С учетом этой замены сохранит свое значение и формула (87), так что вместо соотношения (88) получим:
О
Для проведения интегрирования вместо формулы (90) воспользуемся теперь иным соотношением
F УоШг —■*.(-/в <«*>
О
Где Ко —видоизмененная функция Бесселя второго рода.
Изменяется и выражение для прижимной силы:
Ft = бяпа-^- Уь
С учетом этих изменений получим аналог формулы (99) для случая сферической частицы:
J_ JUL/ V
|
Ко (fAn Vhcr/a |
|
Qsph __ |
|
(105) |
|
Сг |
З у R / Li
Сравнивая формулы (99) и (105), убеждаемся, что зона осаждения в случае сферической частицы примерно в (a/hcr)1/2 Раз шире.
 31 декабря, 2012
31 декабря, 2012  admin
admin 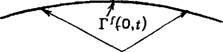
 Опубликовано в рубрике
Опубликовано в рубрике 