Как было показано выше, поверхностная энергия стремится самопроизвольно уменьшиться. Это выражается в уменьшении межфазной поверхности или поверхностного натяжения. К явлениям, происходящим вследствие стремления к самопроизвольному снижению поверхностного натяжения, относится адсорбция. Адсорбция представляет собой процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой. Из сказанного следует, что адсорбция может происходить в многокомпонентных системах и что при перераспределении компонентов в поверхностный слой предпочтительнее переходит тот компонент, который сильнее уменьшает поверхностное или межфазное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры (сгущение, уплотнение), которое часто называют автоадсорбцией.
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению. Она может быть результатом химического взаимодействия компонента с поверхностью вещества (хемосорбция), и тогда поверхностная энергия может даже возрастать на фоне уменьшения энергии всей системы.
Несмотря на то что адсорбция происходит на границе раз — Дела фаз, принято более плотную фазу (фазу, определяющую форму поверхности) называть адсорбентом. Адсорбент может
|
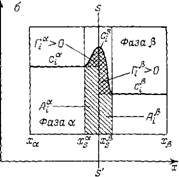
Рис. П.5. Величины адсорбции А. Г и связь между ними. |
S—S" — разделяющая поверхность; а — двухфазная система со слаболдсорбируюшимія компонентом; 6 — двухфазная система с ПАВ
Быть твердым и жидким. Вещество, которое перераспределяется и поэтому обычно находится в газообразной или жидкой фазе, называется адсорбатом. Таким образом, адсорбат адсорбируется на поверхности адсорбента. Обратный процесс перехода вещества из поверхностного слоя в объемную фазу называют Десорбцией.
В зависимости от агрегатного состояния смежных фаз, которое придает определенную специфику явлению адсорбции, различают адсорбцию газов на твердых адсорбентах, адсорбцию растворенных веществ на границах твердое тело — жидкость и жидкость — жидкость, а также адсорбцию на границе жидкий раствор — газ.
Для количественного описания адсорбции применяют в основном две величины. Одна измеряется количеством или массой адсорбата, т. е. числом молей или граммов, приходящимся на единицу площади поверхности или на единицу массы адсорбента (для твердого в порошкообразном состоянии); эту величииу принято обозначать буквой А (метод слоя конечной толщины). Другая характеристика величины адсорбции определяется избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента. Эту величину называют гиббсовской адсорбцией и обозначают буквой гамма Г (метод избыточных величин Гиббса).
|
|
Рис. II.5. иллюстрирует обе величины адсорбции и их различие. На нем представлена двухфазная (фаза а и j5) равновесная система, в которой распределен компонент, адсорбирующийся на межфазной поверхности. Границы фаз в методе слоя конечной толщины обозначены ха, Х(, и xsa, Х/
Поверхностный слой распространяется от х* до х/. Запишем общее число — молей распределяемого компонента (адсорбата) І:
Пі = піа’ + пр’ + пґ (11.36)
Где riia’, nf — число молей адсорбата в фазах без поверхностного слоя; п,"’ — число молей адсорбата в межфазном слое.
Выразим общее число молей адсорбата t через концентрации его в фазах с,, толщину фаз н поверхностного слоя:
N( = tV*UV — Л-а^’ + ГДл—Р — x/)s+ I cfsdx (11.37)’
Va‘ * ®
П;8′ =3 AS
Если использовать метод избыточных величин, то имеем
Т = + + (11.38)5
Где Піа и nf — число молей адсорбата в фазах, включая части поверхностного слоя с концентрациями, равными концентрациям в объеме; т’ — избыток числа молей адсорбата, приходящийся на разделяющую поверхность,, абсцисса которой х8
Или m = CialXs — Xa)s + cfil. XQ — *s)s + ‘ ‘ Vl
Xf
4- j’ (crs — C^sdx-‘r j (c, s — Cissdx (11.39)
Nt*=>rts
Избыточное число молей адсорбата rits можно представить через среднюю концентрацию в поверхностном слое с/, которую можно считать постоянной иа протяжении всей толщины поверхностного слоя. После интегрирования при этом условии сумма интегралов в іравиении (11.39) примет вид:
(<V — Cia)sixs — -Vea) + (Cis — — Xs) (11.40)
Или
Nis=(cis — Cia) + (с/» — С,*) (11.41)
Где V’a* и Vf," — объемы частей поверхностного слоя со стороны фаз соответственно а и р. Для величины гиббсовской адсорбции из уравнения (11.41) получим:
Г(=N,’/s= (a* — C(‘a) Ksa/s+ (сі" — Сі") Ksp/s (11.42)
В простейших случаях, когда адсорбат не переходит в объем одной из фаз (адсорбция иа твердых адсорбентах, адсорбция нелетучего компонента на границе жидкость — газ) уравнение (11.42) приобретает вид
— C,)/S (11.43)
Где V’—.объем поверхностного слоя; с,—концентрация адсорбата в объеме.
В такое же соотношение переходит уравнение (11.42) и при проведении Разделяющей поверхности по одной из границ поверхностного слоя (тогда ^ я"=0 или vy=0).
4t
Для получения соотношения между Л и Г составим балансное уравнение относительно числа молей адсорбата в поверхностном слое:
/4s = ra/s + c, Vs= Г,-s + c, Vs <її.44>
Где CjVе—число молей адсорбата в поверхностном слое без избытка (как в объемной фазе такого же объема).
Из уравнения (11.44) следует
Л,= Г i + aVs/s~ Г i+Cik (П.45>
Где H ■— толщина поверхностного слоя.
Уравнения (11.43) и (11.45) отражают физический смысл величин адсорбции Л и Г и различия между ними. Однако эти уравнения нельзя использовать для определения величин адсорбции по экспериментальным данным, так как остаются неизвестными объем и толщина поверхностного слоя. Чтобы получить необходимое соотношение, составим балансное уравнение относительно числа молей адсорбата во всей системе до и после адсорбции:
Vco=V"Ci+V4is (11.46*
Где V н V" — общий объем системы и объем фазы без поверхностного слоя; Со — исходная концентрация компонента г.
Подставим в уравнение (11.43) соотношение (11.46), исключив число молей адсорбата в поверхностном слое, т. е. Vsc, s: Г; = Vs (с ,S — D) /S = (V‘Ci‘ — Vs С,) /S =
= (Vc0 — V"a — V*c<) /s (II.47> Так как то
Гі = [Ус0— Ivv+ V*)Cii/s=(Vc0— Va)/S (11.48)
Или Г,-= Vlco — ы) /s (II.49>
Все величины, входящие в уравнение (11.49), могут быть установлены экспериментально. Это соотношение широко используется для расчета величины гиббсовской адсорбции. Значительно сложнее определить величину адсорбции Л. (Расчет этой величины рассматривается в разделе, посвященном адсорбции из растворов.) Если концентрации адсорбата в поверхностном слое значительно больше, чем в объеме и Л «Г (11.45), то для определения Л также используют уравнение (11.49).
Из соотношения (11.49) также следует, что величина гиббсовской аДСОрбцИИ МОЖеТ бЫТЬ И МеНЬШе НуЛЯ, ЄСЛИ С0<Сі, В противоположность величине Л, которая никогда не может Быть отрицательной.
На рис. II.5 величина А соответствует всей заштрихованной площади под кривой профиля концентрации в поверхностном слое, а величина Г составляет площадь с двойной штриховкой (площадь, ограниченная кривой концентрации в поверхностном слое и прямыми, отражающими концентрации адсорбата в объемных фазах.
При установлении адсорбционного равновесия в системе количество адсорбированного вещества в поверхностном слое находится в определенной зависимости от концентрации или парциального давления этого компонента в объеме и от температуры. Согласно правилу фаз Гиббса число параметров, определяющих состояние системы, равно
Р=К—Ф+2 (11.50)
Где F — число степеней свободы; К — число компонентов в системе; Ф — число фаз; 2 — два параметра: давление и температура.
В простейшем варианте адсорбции из газовой фазы система состоит из адсорбента и газа-адсорбата. Для этой системы число компонентов равно 2, число фаз составляет 2 и в соответствии с правилом фаз Гиббса (11.50) число степеней свободы также равно 2. Это значит, что можно произвольно изменять два параметра: давление и температуру, при определенных значениях которых достигается равновесное состояние системы. Если система состоит из конденсированных фаз (твердой и жидкой), то адсорбируется растворенное вещество и число компонентов в ней будет равно 3. Обычно для конденсированной системы пренебрегают влиянием давления, и тогда в ней число степеней свободы также оказывается равным 2: концентрация и температура.
Таким образом, любой из параметров системы однозначно может быть определен как минимум через два других параметра. Из приведенных примеров следует, что этими параметрами могут быть концентрация (давление) адсорбата и температура. Относительно величины адсорбции А уравнение состояния адсорбционной системы имеет следующий общий вид:
Л=/(с, г)=ч'(р, г) (11.51)
Где с н р — соответственно равновесная концентрация и парциальное давление адсорбата; Т — температура.
Из соотношения (11.51) следует, что возможны три вида зависимости величины адсорбции от параметров системы. Зависимость величины адсорбции от концентрации (или парциального давления) вещества при постоянной температуре называется изотермой адсорбции:
Л=/Г(с)=фг(р) (11.52)
Зависимость величины адсорбции от температуры при постоянной концентрации (или парциальном давлении) вещества называется изопикной (или изобарой) адсорбции:
Л=д(г)=(р„(г) ш.53)
4а
Зависимость концентрации (или парциального давления) вещества в объеме от температуры при постоянной величине адсорбции называется изостерой адсорбции:
Г=/.4(Л или р = фл(Л (11.54)
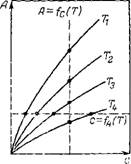
Постоянство температуры обеспечивать, безусловно, проще, поэтому наиболее распространенной зависимостью, получаемой экспериментально, является изотерма. Другие две зависимости можно графически построить из серии изотерм, полученных при различных температурах. На рис. II.6 показано, что система точек пересечения изотерм прямой, параллельной осн ординат, соответствует изопикне, а при пересечении изотерм прямой, параллельной оси абсцисс, получаются точки изостеры. По полученным точкам строят зависимости величины адсорбции (изо — пикна) или концентрации (изостера) от температуры.
Покажем, что изотерма, изопикна, изостера связаны математически. Из уравнения (11.51) следует, что полный дифференциал от величины А, как функции состояния, может быть выражен через частные производные:
|
(1Т |
|
ДТ |
Ал N. / дА
<1А:
Если принять постоянной величину А, то
|
ДА дТ |
|
ДА ДТ |
|
ДА |
|
ДА_ дс |
|
І Дс_ дТ |
|
(де) Л |
|
Т, |
|
! О или |
|
>0 |
|
Дс |
|
}т |
Умножив обе части последнего соотношения на (ДТ/дА), получим:
|
(11.55) |
|
Ас |
ДА ( дс ! дТ
ДТ! л дА
Это хорошо известное математическое соотношение широко применяется в термодинамике. В данном случае частные производные представляют собой изотерму, изостеру и изопикну соответственно, а уравнение (11.55) выражает дифференциальное
|
Fl=const |
|
T,-const |
Соотношение между ними. Оно позволяет найти любую из производных, если известны остальные. Можно определить знаки этих производных. Производная (ДА/дс)т Всегда положительна, это объясняется тем, что химический потенциал и соответственно активность адсор-
Рис. II.6. Построение изостер c—fA(T) И пзопнкн A=Jc(T) по изотермам адсорбции A — fT(c).
Бата с установлением равновесия выравниваются во всей системе. Отсюда с увеличением концентрации (давления) адсорбата в объеме растет его концентрация в поверхностном слое, т. е. величина адсорбции А. Таким образом, две другие производные имеют разные знаки. Необходимо отметить, что па аналогичных зависимостях гиббсовской адсорбции Г, как избытка вещества на поверхности, могут наблюдаться максимумы и минимумы.
Уравнение состояния адсорбционной системы [см. уравнение (11.51)] можно записать и относительно поверхностного (межфазного) натяжения:
О=/(г, Л=ф(р, Г) (II.5G)
|
Тогда дифференциальное соотношение будет иметь вид
|
Из сравнения (11.51), (11.55) с (11.56) и (11.57), видно, что существует четкая связь между величиной адсорбции и поверхностным натяжением.
 2 ноября, 2012
2 ноября, 2012  admin
admin 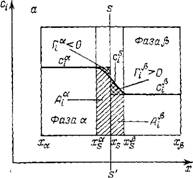
 Опубликовано в рубрике
Опубликовано в рубрике 