Растворы высокомолекулярных соединений — термодинамически устойчивые (лиофильные) коллоидные системы. В соответствии с закономерностями образования лиофильных систем процесс растворения полимеров происходит самопроизвольно
Рис. VI.12. Зависимость давления пара растворителя от его мольной доли в растворе полимера
(самопроизвольное диспергирование). Термодинамическая устойчивость, обратимость лиофильных коллоидов указывают на возможность применения к таким системам правила фаз Гиббса в той же форме, что _ и для истинных растворов, а значит, и всех термодинамических соотношений.
Экспериментальные исследования показывают, что полимеры растворяются в низкомолекулярных растворителях, как правило, с небольшим тепловым эффектом, но в то же время образуют растворы, для которых характерно сильное отрицательное отклонение от идеальности. На рис. VI. 12 показана зависимость давления пара растворителя от егб мольной доли в растворе полимера. Так как определение отклонений от идеальности растворов полимеров удобнее проводить по изменению активности растворителя аи то в качестве основного термодинамического уравнения, описывающего состояние раствора полимера, чаще всего принимают выражение для осмотического давления (IV.45) и как следствие — уравнение с вириальными коэффициентами (IV.48), являющееся одним из уравнений состояния растворов полимеров
K/c=RT(AX+A2C+AIc2+ …)
Здесь необходимо отметить, что для растворов полимеров второй вириальный коэффициент выражают чаще в виде следующей формулы [помимо соотношения (IV.49)]:
A2~VoNa/{2M22) (VI.71)
Где Vo — объем, из которого сегменты одних макромолекул вытесняют сегменты других макромолекул (так называемый эффективный исключенный объем); NA—число Авогадро; М2 — молекулярная масса полимера.
Исследования растворов полимеров показали, что характер — лое для них сильное отрицательное отклонение от идеальности связано с различием в размерах молекул ВМС и растворителя и особенно с гибкостью линейных макромолекул, которые значительно увеличивают энтропию смешения при растворении. Вклад конформаций макромолекул в энтропию смешения был учтен в теории растворов полимеров, в основе которой лежит уравнение Флори и Хаггинса, полученное с помощью статистической-термодинамики.
|
|
Известно, что из всех возможных состояний системы наиболее вероятны те, которые реализуются наибольшим числом положений молекул в системе. Такое состояние системы отвечает состоянию равномерного рассеяния веществ по всему объему системы, поэтому энтропия при смешении, например двух жидкостей, обязательно увеличивается. Это означает, что термодина
мическая вероятность состояния однородной смеси выше вероятности состояния разделенных веществ.
Если растворитель и растворенное вещество имеют одинаковые по размеру и форме молекулы, а взаимодействия между ними одинаковы при всех сочетаниях молекул, то смешение будет идеальным. Оно будет совершаться только благодаря росту энтропии:
A‘Sc— — — (я, 1п ^^ + л, In (VI .72)
Где AS см — энтропия смешения; кв—константа Больцмана; щ и п2— число молекул растворителя и растворенного вещества соответственно.
Как видно из уравнения (V1.72), изменение энтропии зависит только от числа смешиваемых молекул или от их концентрации. Если предположить, что масса растворенного вещества остается той же, а его молекулярная масса увеличивается, например в результате полимеризации, то должно уменьшаться число его молекул, т. е. частичная концентрация. В соответствии с уравнением (VI.72) уменьшение числа частиц в системе должно уменьшать приращение энтропии. Такие рассуждения привели в свое время к ошибочным выводам о том, что растворение ВМС и иеидеальность их (растворов обусловлены изменением внутренней энергии, хотя очевидно, что іпростое увеличение размера молекул без изменения их качества не может существенно изменить характер взаимодействия с растворителем.
В дальнейшем методом статистической термодинамики было показано, нто энтропия смешения значительно увеличивается, если смешиваются не одинаковые молекулы, а различающиеся по размерам и форме, и особенно если молекулы одного из компонентов обладают гибкостью. В такой системе возрастает число возможных расположений молекул относительно друг друга. Действительно, длинная н гибкая макромолекула может располагаться среди небольших молекул растворителя огромным числом способов в результате теплового движения отдельных звеньев цепи.
Для определения энтропии смешения линейного полимера с иизкомолеку — лярным растворителем необходимо предположить, что размер сегментов макромолекулы (звенья) равен размеру молекулы растворителя. Иногда в качестве сегмента берут мономерную единицу, а за их число z в цепи макромолекулы принимают степень полимеризации. Используя решеточную модель раствора, в которой отдельные узлы решетки заняты молекулами растворителя или сегментами макромолекулы, обладающей гибкостью, рас — !читывают число возможных расположений макромолекул. Число частиц, принимающих участие в перестановках, равно п=щ + п2г. После расчета полной статистической вероятности Q в соответствии с уравнением Больцмана определяют энтропию смешения:
Или
ASCu=— In фі+"2 In ф2) (VI.74)
Где фі и ф2объемная доля растворителя и растворенного вещества соответственно.
Сопоставляя уравнения (VI.73) и (VI.72), можно заметить некоторую аналогию. В растворе полимера каждый сегмент макромолекулы ведет себя почти как самостоятельная частица. Ограничение числа степеней свободы, обусловленное связыванием сегментов в единую макромолекулу, выражается только в том, что перед логарифмом, относящимся ко второму компоненту (полимеру), стоит число молекул полимера п2 вместо произведения
IfeZ.
Чтобы перейти к уравнению, в котором содержание вещества в системе выражено в молях, необходимо правую часть уравнения (VI.74) умножить и разделить на число Авогадро:
ASC„=— R(N, In <p,+jV2ln <p2) (VI.73)
Где N1 и JV2 — число молей компонентов.
Полученная формула определяет чисто конфигурационную энтропию, т. е. учитывает только перемену положений молекул растворителя и звеньев цепи макромолекул в растворе. Растворы, отвечающие только таким условиям их образования, называются атермическими (при смешении не происходит изменения внутренней энергии — тепловой эффект равен нулю). Чтобы данную теорию можно было применить к реальным растворам полимеров, имеющим небольшие отклонения от строго атермических растворов, предложено учитывать изменение внутренней энергии с помощью теории регулярных растворов. В отличие от атермических растворов для регулярных растворов энтропия смешения принимается равной энтропии при идеальном смешении, а неидеальность системы обусловлена только изменением внутренней энергии (межмолекулярным взаимодействием).
В соответствии с теорией регулярных растворов изменение парциальных внутренних энергий для обоих компонентов соответственно равно
ДГ^ВЇЛф^ It Ш2=в%Фг, (VI.76)
В= </д—/дE2/V2)*= (б, — б2)г
Где Д£| и ДЕ? — энергия испарения 1 моль первого и второго компонентов соответственно; б — параметр растворимости по Гильдебранду; Vi и F2—парциальные мольные объемы компонентов 1 и 2.
Чтобы получить значения парциальных энтропий смешения компонентов, необходимо продифференцировать уравнение (VI.73) по числу молей (молекул) этих компонентов:
AS^dAScJdn^— Я[1п (1— ф2> + <1 — l/z)<p2] (VI.77)
ASi=dASct,/dn2=— Я[1п (1 — <pi) + (z— Пері] (VI.78)
Объединяя эти уравнения с соответствующими уравнениями (VI.76), получим:
Aii=AGl = AHi — TASi=RTn (I —Ф2) +
+ RT(l-l/z)<p2+BVm* (VI.79) Дц2=Д52=ДЯг — TAS2=RT In (1 — ф,) +
■+RT(z— Dtft+BV^h (VI.80)
Для растворителя активность и соответственно химический потенциал можно определить экспериментально, например по давлению пара. Тогда выражение (VI.79) целесообразно представить относительно осмотического давления;
Я=-Дц,/К,————— («Г/?,) [In (1-ф2) +
+ (1—1/2)ф2+х. Ф22] (VI.811
-тде Xi-flF,/U? n
Выражение (VI.81) является уравнением состояния растворов полимеров — основным соотношением в классической теории Флори — Хаггинса. Поскольку молекула полимера была приията в z раз больше молекулы растворителя, то
/z=Vx/V2 (VI.82V
При очень большой величине Z значением /г в уравнении (VI.81) можно пренебречь.
Константа Xi характеризует взаимодействие полимера с растворителем: ее называют константой Хаггинса. Она определяется с помощью различных экспериментальных методов. Константа Хаггинса непосредственно связана со вторым внриальным коэффициентом А2. Чтобы это показать, проведем небольшие преобразования уравнения состояния (VI.81). Разложим в ряд логарифмический член, включая второй член ряда, и учтем соотношение ^(VI.82). Получим:
|
, 2I Ф2 + ХіФ 2 = |
|
RT |
|
Г* , — Ф2 — — О — + Ф2 |
RT RT ! 1
|
Так как |
Ф2 + !Г — ЬГ-ХІ1Ф22 (VI .83)
К2 ^ Vx { 2
V2 = M2/p2, V = M/р1 И ф2=С2/р2, TO я RT RTpx ( 1
Ъ)* (VI-84)
Где Ліі и М2 — молекулярная масса растворителя и полимера соответственно; Pi и Рг — плотность растворителя и полимера соответственно.
Сравнивая уравнение (VI.84) с уравнением состояния (IV.48), найдем:
— ‘ — — *і І (VI .85)
Р2;
Таким образом, константа Хаггииса и второй вириальный коэффициент явлиются мерой сродства между компонентами раствора. Чем сильнее взаимодействие (лучше растворитель), тем больше А2 и тем меньше Xi — При идеальном растворении А2 = 0, Xi= ‘/г — Как известно, степень отклонения от идеальности зависит и от температуры. Это отражается на значении параметра Хі в (VI.81). Если выражение для /і подставить в соотношение (VI.85), то получим:
‘ — Р1(1~9/Г) в—^ (VI .86)
2ІМіР»,
Параметр 0 выражаетси в единицах температуры и называется характеристической температурой Флори. При Т = 0 Л2=0, т. е. параметр 0 — это такай температура, при которой для реального раствора не наблюдается отклонений от идеальности. Ее можно определить как отношение избыточной энтальпии к избыточной энтропии Q = HE/SE, так как при идеальном смешении GE=HE—0SЈ = O. Характеристическую температуру Флори определяют по температурной зависимости второго вириального коэффициента А2, Экстраполируя ее к значению А2= 0.
Из теории Флори — Хаггинса следует, что растворение полимера в хороших растворителях сопровождается существенным уменьшением энергии Гиббса, что обусловлено как выделением теплоты (ДЖО), так и ростом энтропии. Для таких систем Л2>0 и зо<72 (отрицательное отклонение от идеальности). Это означает, что силы отталкивании между макромолекулами в растворе полимера определиются энтропийной составляющей и взаимодействием с растворителем. В плохих растворителях (І42<0) происходит поглощение теплоты (Д//>0), и силы отталкивания между макромолекулами имеют исключительно энтропийную природу; рост энтропии полностью перекрывает рост энергии Гиббса вследствие межмолекулярного взаимодейст
вия. В этих системах возможно достижение температуры Флори (положительная энтальпия смешения компенсируется избыточной энтропией), ниже которой преобладают силы притяжения между макромолекулами (А2<0).
Теория Флори — Хаггинса позволила объяснить большие отклонения от идеальности растворов полимеров. Она удовлетворительно согласуется с экспериментальными данными для растворов, получение которых сопровождается небольшими тепловыми эффектами. Однако ряд экспериментальных фактов еще ждет объяснения, несмотря на постоянное совершенствование теории.
Роль размера частиц дисперсной фазы в обеспечении устойчивости растворов полимеров связывает их с другими коллоидными системами. Можно утверждать, что системы с компактными сферическими частицами дисперсной фазы проявляют отклонения от идеальности хотя и меньшие, чем системы, содержащие линейные макромолекулы, но эти отклонения все равно остаются отрицательными. Таким образом, только различие в размерах частиц дисперсной фазы и молекул дисперсионной среды (вносит вклад в энтропийный фактор устойчивости коллоидных систем. Этот вклад возрастает для лиозолей, стабилизированных с помощью ПАВ и особенно высокомолекулярных соединений.
 2 ноября, 2012
2 ноября, 2012  admin
admin 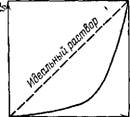
 Опубликовано в рубрике
Опубликовано в рубрике 