Ультрамикроскопия отличается от обычной микроскопии тем, что исследуемый объект, в частности, дисперсная система, освещается сбоку мощным потоком света. Наблюдают рассеянный свет частицами, взвешенными в среде с иным показателем преломления. По существу образуется как бы конус Тиндаля от каждой частицы. Так как интенсивность падающего света значительно выше интенсивности рассеянных лучей, то главным условием возможности наблюдения в микроскопе частиц является отсутствие распространения падающего света в направлении рассеянных лучей. Частицы кажутся светящимися точками на темном фоне, даже если их диаметр намного меньше разрешающей силы объектива микроскопа. Кажущийся диаметр частицы равен сумме ее действительного диаметра и разрешающей силы микроскопа (V. 1). Применение ультрамикроскопа позволяет наблюдать движение частиц, подсчитывать их число и определять размер частиц диаметром до 2—3 нм.
Чувствительность ультрамикроскопии очень сильно зависит от интенсивности падающего света (освещенности поверхности частиц) и от длины волны, но возможные интервалы этих параметров ограничены другими факторами, не имеющими отношения к оптике (например, опасностью сильного нагревания и разложения образцов). "
Ультрамикроскоп был сконструирован в 1903 г. австрийскими учеными Зидентопфом и Зигмонди, и с этих пор стало возможным исследовать ультрамикрогетерогенные (диаметр частиц меньше 100 нм) системы. Значение этого событий для развития коллоидной химии и всей науки в целом огромно. Так, основополагающие в коллоидной химии работы Перрена и Свед — берга были выполнены ими с использованием ультрамикроскопии.
Ультрамикроскопия может быть использована для исследования любых дисперсных систем независимо от агрегатного состояния фаз. В этой связи интересно отметить, что внешним поводом для открытия ультрамикроскопии явилось исследование рубиновых стекол, которое проводили Зидентопф и Зигмонди.
Наиболее простым является щелевой ультрамикроскоп, схема которого представлена на рис. V.3. В более совершенных приборах применяются специальные приспособления для освещения объектов исследования. Например, вместо щелевой диафрагмы, которая недостаточно использует источник света и направляет его лучи на объект только с одной стороны (из-за чего искажается форма частицы), широкое применение нашли конденсоры темного поля, устанавливаемые в простом микроскопе для создания бокового освещения.
|
Рис. V.3. Схема хода лучей в щелевом ультрамикроскопе: 1 —- световой поток; 2 — щелевая диафрагма; 3 — фокусирующая линза; 4 — кювета с исследуемым золем; 5 — объектив; 6 — окуляр |
Рис. V.4. Схема хода лучей в конденсоре темного поля:
1 — световой поток; 2—центральная диафрагма; 3 — плоско-выпуклые лнизы; 4—кювета с исследуемым золем
Один из вариантов конденсоров темного поля представлен на рис. V.4. Центральная диафрагма 2 препятствует прямому падению света на объект 4. Проходящие боковые лучи 1 отражаются от поверхностей плоско-выпуклых линз 3, выпуклая поверхность которых представляет собой параболоид вращения. Лучи фокусируются на поверхности предметного стекла. При такой конструкции конденсора увеличивается не только интенсивность освещения частиц, но и площадь ее освещенной поверхности, что дает возможность наблюдать форму частиц. Частицы неправильной формы (анизометрические) мерцают, так как при их вращении в процессе теплового движения в глаз наблюдателя поступает разное количество рассеянного света. Это обусловлено тем, что рассеяние света наиболее интенсивно в направлении падающих лучей, совпадающем с длиной вытянутой частицы. Во всех остальных направлениях светорассеяние гораздо слабее Когда частицы, находящиеся в беспорядочном тепловом движении, случайно располагаются перпендикулярно — к падающему лучу, яркость их свечения резко увеличивается, т. е. происходит как бы их вспыхивание. Такая вспышка отчетливо видна при наблюдении поведения достаточно «состарившихся» золей пятиоксида ванадия, оксида железа и др. Это явление очень хорошо наблюдается в кардиод-конденсоре с азимутной диафрагмой, позволяющей изменять направление падающего луча.
Определив с помощью микроскопа число частиц в пробе, по формулам (V.2) легко рассчитать их размер, предположив сферическую или кубическую форму частиц. Для этого необходимо — знать общую массу частиц в пробе и их плотность. При известных массовых с и частичных v концентрациях уравнения (V.2),
|
(V.9 |
3 3 —
Г е= у’ Зс/(4лгр) и 1^=-/c/(vp)
Где /— размер ребра кубиков, за которые приняты частицы.
Размер частиц можно рассчитать по измеренному расстоянию х между ними. Если принять частицы за кубики объемом I3, а пустоты между частицами за параллелепипеды объемом 12х, то размер частиц будет равен
1=сх/( р •— с)
Расстояние между частицами определяют с помощью окуляр — микрометра.
Ранее только опытные исследователи могли получать удовлетворительные результаты при ультрамикроскопических исследованиях, что было связано с большими трудностями определения параметров, входящих в расчетные формулы. Например, достаточно сложная операция — определение объема образца. Не менее сложен и очень утомителен подсчет частиц. Чтобы получить удовлетворительные результаты, исследователям приходилось выполнять сотни и тысячи отдельных определений.
|
Можно представить в следующем виде: |
В настоящее время созданы приборы, довольно сложные по конструкции, автоматически выполняющие практически все операции. Одним из таких приборов, предложенным отечественными учеными Б. В. Дерягиным и Г. Я. Власенко, является поточный ультрамикроскоп. Золь протекает через специальную кювету в направлении оси микроскопа при боковом освещении. Проходя освещенную зону, каждая частица золя дает вспышку, которая регистрируется счетчиком. По различной яркости частиц их можно разделить на фракции и построить кривые распределения.
В результате интегрирования в пределах от /0 до / и соответственно от х = 0 до I — толщины слоя системы, получим:
In (/0//п) =т/ или Іп — ІаЄ~г1 (V.10)
Где /„ — интенсивность света, прошедшего через систему.
При выводе предполагалось, что изменение интенсивности света происходит только за счет рассеяния. Поэтому уравнение (V.10) справедливо для систем, которые не поглощают свет, т. е. для так называемых белых золей. Если золи еще и поглощают свет, то к величине т необходимо прибавить коэффициент поглощения. Как следует из уравнения (V. 10), мутность измеряется в единицах длины в минус первой степени. Ее можно рассматривать как величину, обратную расстоянию, на котором интенсивность света снижается в е раз, т. е. до 37% от первоначального значения. Например, для 1%-ного раствора полимеров это расстояние составляет около 10 м, а для чистых жидкостей— около 1 км.
В соответствии с уравнением (V. 10) мутность связана с оптической плотностью D соотношением:
1п (/о//„) =т/=2,3 Lg (/о//,:) =2,3D (V.1I»
Интенсивность прошедшего света можно представить в виде разности
/п = /О-/’Р
Где /’р — интенсивность света, рассеянного образцом длиной /.
Разделив на /0 и логарифмируя, получим:
—2,3D=Ln[L— (/’,//„>] (V.12)
Принимая во внимание, что 11Р<^10, разлагая в ряд логарифм и пренебрегая бесконечно малыми величинами второго рорядка, лолучим:
2,3D « /’р//0=/р///0=т/ " (V.13)
Из сравнения уравнений (V.13) и (V. 11) следует, что мутность выражается отношением интенсивностей рассеянного и падающего света, отнесенным к единице длины образца. Это отношение в соответствии с уравнением Рэлея (V.5) равно:
T=kcv/*=kvv2/V (V.141
Где K — константа, включающая постоянные параметры в уравнении Рэлея. Подставляя полученное выражение мутности в (V.13), получим:
D=*k‘cvl/X*=*k‘xv4/W (V.15*
При постоянных к и I уравнение (V.15) можно записать в виде
D—k"co—k"wz (V.16»
Где к" — константа, ие зависящая от с и и.
Более строгий вывод дает следующее выражение вместо соотношения (V. 15):
/ см
Где D — диаметр частиц; а — константа, зависящая от природы золя.
Если принять во внимание, что уравнение Рэлея справедливо при условии d^O. lX, то членом d4 в знаменателе уравнения (V.17) можно пренебречь, тогда оно переходит в (V.15).
Из формулы (V.16) следует, что оптические плотности двух золей с одинаковыми размерами частиц относятся как частичные концентрации сравниваемых дисперсных систем; при одной и той же объемной концентрации систем оптические плотности относятся как объемы частиц или кубы их диаметров (радиусов) :
При V = const
Di/Di^Vi/^Ci/a (V.18>
И при с=const *
Dl/D2=vl/v2=d3l/d32 (V.19)
Если дисперсная система содержит частицы, размер которых больше, чем 0,1А, то помимо увеличения интенсивности рассеяния в направлении падающего света и уменьшения ее в обратном направлении проявляются отклонения от закона Рэлея. Эти отклонения обусловлены другой зависимостью рассеяния света ■от длины волны и поляризационными явлениями. Они могут быть использованы для оценки размеров частиц. С увеличением размеров частиц интенсивность рассеяния становится обратно пропорциональной длине волны в степени, меньшей, чем четвертая. Поэтбму Геллер предложил выразить оптическую плотность и мутность следующими формулами вместо (V.14) и (V.15)
D^kl-" и <V.20>
^где k и k’ — константы, не зависящие от длины волны.
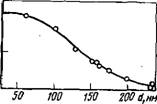
Зависимости lgt (или lgЈ)) от lg Я в соответствии с уравнениями (V.20) представляют собой прямую, отрицательный тангенс угла наклона которой равен показателю степени п, т. е. 4
П
Рис. V.5. Зависимость показателя степени при длине волны в уравие — J
|
|
Нии Геллера от диаметра сферических диэлектрических частиц
Для рэлеевского рассеяния и меньше четырех для светорассеяния большими частицами. По градуировочному графику (рис. V.5), построенному предварительно, например по результатам электронно-микроскопического исследования, экспериментально определив величину я в соответствии с формулами Геллера, можно найти размер частиц.
Необходимо отметить, что для явления истинного рассеяния показатель степени л не может быть больше четырех, при наличии же истинного поглощения значение л может быть значительно больше.
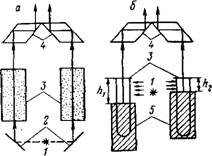
Преимущество турбидиметрического метода исследования состоит в простоте методики измерений. В качестве турбидимет — ра — прибора для проведения турбидиметрических измерений можно использовать широко распространенные фотоэлектроко — лориметры (рис. V.6a), предназначенные для определения оптической плотности окрашенных молекулярных растворов. В основу действия большинства фотоэлектроколориметров положен принцип уравнивания двух сравниваемых световых потоков, проходящих через кюветы с исследуемым и стандартным золями с помощью переменной щелевой диафрагмы.
Точность турбидиметрического метода небольшая, поскольку интенсивность рассеяния (относительно малая величина) определяется по разности двух больших значений интенсивностей падающего и проходящего света. Применение метода ограничивается золями, отличающимися сравнительно высокой мутностью.
Рис. V.6. Принципиальные схемы турбидиметра (а) и нефелометра (б):
.1 — источник света: 2 — зеркала; 3 — кюветы с исследуемым золем; 4 — призмы; 5 —подвижные экраны
Из этого соотношения следует, что интенсивность света, рассеянного двумя золями с частицами одинаковой формы и одинаковых размеров, относятся между собой как концентрации частиц определяемого вещества. Если же в сравниваемых золях объемные или массовые концентрации равны, то интенсивности рассеянного света (мутности золей) будут относиться как объемы частиц или кубы их диаметров
Прн v=const
W/p2=T,/Tj=v,/v2 (V.21I
При с=const
/рі//м=ТІ/Т2=О,/О2=ЙР,/<*92 (V.22>
Таким образом, имея стандартные золи (или градуировочиые кривые), легко определить размер частиц и концентрацию исследуемого золя (при постоянной данной длине волны).
Нефелометрия широко применяется для определения молекулярных масс макромолекул. В основе таких измерений лежит соотношение (V.14), приведенное к виду:
Kcm kMc
Тде m — масса макромолекулы; М — молекулярная масса полимера; NA — "число Аиогадро; р — плотность полимера.
Отсюда молекулярную массу для идеальных систем можно •определить по уравнению
Л*=т/(Яс) (V.24)
|
|
Где H=kf(NKp)
|
305 |
Если с принять за массовую концентрацию, то в знаменатель уравнения будет входить плотность в квадрате. Результаты анализа в данном методе могут иметь погрешности, обусловленные взаимодействием между макромолекулами в растворах. Для исключения этих погрешностей при определении молекулярной массы полимеров, мицеллярной массы ПАВ или просто массы частиц осмотически активных золей вместо метода сравнения Применяют абсолютный метод Дебая. Интенсивность рассеянно — то света в этом методе выражают уравнением Эйнштейна, которое получается на основе учета флуктуаций оптической плотности, возникающих при изменении осмотического давления и кон-
20 Фролов ю. г.
Центрации. Так как основной причиной изменения интенсивности флуктуации концентраций является изменение осмотического давления, то это дает возможность связать соотношения для рассеяния света и осмотического давления. Используя уравнение •осмотического давления до второго вириального коэффициента А2, учитывающего взаимодействие частиц с растворителем, Дебай получил следующее соотношение между мутностью раствора полимера, его концентрацией и молекулярной массой:
Яс/т=1/М + 2Л2с (V.25)
Где Я — константа Дебая, имеющая тот же физический смысл, что и константа в уравнении (V.24).
Значение константы Н в этом уравнении равно
32 nW(dn/dcV
Яс= Щ5 (V-26>
Где л и по — показатель преломления раствора и растворителя соответственно.
С помощью прямой, построенной в координатах Нс/х-^-с в соответствии с уравнением (V.25), можно определить 1 /М и
Этот метод является абсолютным, не требующим калибровки, так как в константу Дебая Я входят либо известные величины X, Na, либо измеряемые п и Dn/Dc. Показатель преломления раствора с достаточной степенью точности можно считать равным показателю преломления растворителя, л=л0. Производная Dnjdc должна быть измерена с большой точностью { в уравнение (V.26) входит ее квадрат], что достигается с помощью интерферометра. Метод дисперсионного анализа, основанный на измерении светорассеяния, дает среднее объемное (массовое) значение массы (или размера) частицы.
Этот метод позволяет оценивать также форму и конформации частиц (макромолекул), если их размеры сопоставимы с длиной световой волны. Для этого необходимо измерить значения интенсивности света, рассеянного под разными углами. Основная экспериментальная трудность измерений заключается в очистке исследуемых объектов от пыли, создающей недопустимый фон рассеянного света. Для этой цели обычно используют стеклянные и полимерные фильтры.
Принципиальная схема нефелометра (тиндалиметра) приведена на рис. V.6б. Прибор аналогичен фотоэлектроколориметру. Принципиальное отличие состоит в том, что в нефелометре источник света располагается так, чтобы падающий световой поток был направлен — под углом к потоку регистрируемого рассеянного света. Для установления абсолютных значений интенсивности света при исследовании формы частиц и межчастичных взаимодействий на дальних расстояниях применяют монохроматический свет (например, излучение ртутной лампы). Кроме
того, в приборе предусмотрена возможность регистрировать интенсивность рассеянного света под разными углами. Прибором для регистрации интенсивности света служит фотоумножитель.
 2 ноября, 2012
2 ноября, 2012  admin
admin 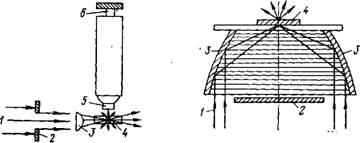
 Опубликовано в рубрике
Опубликовано в рубрике 