Лако-красочные материалы — производство

Удерживание газов и паров пористыми телами, т. е. их адсорб­ционная способность, зависят как от природы взаимодейству­ющих тел, так и от структуры пористого тела. Если структур­ный фактор для макропористых адсорбентов имеет малое зна­чение, то уже для переходнопористых тел его роль резко воз­растает. Это обусловлено в первую очередь проявлением ка­пиллярных сил, действие которых с ростом дисперсности тела непосредственно связано со сродством адсорбата к адсорбен­ту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что такое сродство должно быть достаточ­
ным, чтобы поверхность пористого тела смачивалась жид­костью, появляющейся в результате конденсации пара в порах. Только при условии смачивания капиллярные силы будут втя­гивать адсорбат в поры и обеспечивать адсорбционную спо­собность пористого тела. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. В противном случае (ес­ли поверхность не смачивается) наблюдается капиллярное выталкивание вещества из пор, адсорбция на несмачиваемы. ч телах минимальна и возможна только на ровной поверхности н в крупных порах.

Адсорбция на переходнопористых телах происходит в ос­новном по механизму капиллярной конденсации. Капилляр­ная конденсация начинает проявляться при определенной сте­пени заполнения адсорбента или при определенном значении давления пара, характерном для данной системы. К этому мо­менту поверхностная энергия адсорбента практически пол­ностью скомпенсирована в результате полимолекулярной ад­сорбции, а микропоры заполнены адсорбатом. С увеличением давления газа или пара конденсация происходит и в более крупных порах, радиус мениска жидкости г в которых нахо­дится в соответствии с уравнением капиллярной конденсации Кельвина (отрицательная кривизна):

In ip,/p)=2aVM/lrRT) (III.72і

Из этого уравнения следует, что при смачивании, обеспе­чивающем отрицательную кривизну мениска конденсата (во­гнутый мениск), конденсация в порах наступает при давлении, меньшем давления насыщенного пара, т. е. при Plps< 1.

Выражение для адсорбционного потенциала (11.82) позво­ляет представить соотношение (III.72) в виде

Е = 2 а’я/г (III. 73>

Из которого следует, что адсорбционный потенциал в теории капиллярной конденсации принимается равным капиллярному потенциалу. В уравнении (III.73) связь адсорбционного потен­циала со структурой и природой адсорбента выражается в ви­де простой (обратно пропорциональной) зависимости от радиу­са мениска конденсата в порах. Остальные параметры, опре­деляющие адсорбционный потенциал, относятся только к кон­денсату. Очевидно, что только при полном смачивании радиус мениска можно приравнять радиусу поры; в общем же случае тп = г cos В, где В — угол смачивания.

Для адсорбентов с переходными порами характерна изо­терма адсорбции с петлей капиллярно-конденсационного ги­стерезиса (рис. III.11). Адсорбции соответствует нижняя кри­вая, а десорбции — верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюда-
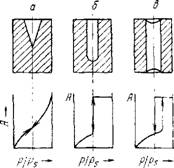
етс-я. Начало появления гистерезиса зависит от природы ад­сорбента и адсорбата. Пористая структура адсорбента разно­образна, однако считается, что ее можно смоделировать сле­дующими тремя видами пор: конусообразными, цилиндричес­кими с одним открытым концом, и цилиндрическими с двумя открытыми концами (рис. III.12). Конденсация в конусообразных порах начинается со дна пор, где кри­визна наибольшая. По мере заполнения поры радиус ме­ниска увеличивается (уменьшается кривизна), поэтому дли дальнейшего заполнения поры необходимо увеличивать давление (рис. III.12 о). Процесс чесорбшш идет в об­ратном направлении и описывается той же кривой. В цилинд­рических норах с одним открытым концом конденсация начинается также со дна пор, где кривизна сферическая и по­этому наибольшая (рис. 111.126). Так как пора цилиндриче­ская, то она заполняется целиком при определенном постоян­ном радиусе мениска, что отвечает и определенному постоянно­му давлению пара. Капиллярная конденсация в этих порах" также происходит обратимо. Йсли у цилиндрической поры тех же размеров оба конца открытые (рис. 1П.12в), то конденса­ция начнется на стенках цилиндра, имеющего кривизну в два раза меньше, чем у сферы того же радиуса. Поэтому заполне­ние поры происходит при большом давлении пара в соответст­вии с соотношением

In t/h/p) = О ІЛ/ (rRT) Пли Е = a VJr

Конденсация па стенках цилиндрической поры приводит к уменьшению диаметра поры, что вызывает ее мгновенное за­полнение при давлении, отвечающем началу конденсации. На концах поры образуются сферические мениски жидкости. Де­сорбция может начаться только при давлении, соответствую­щем радиусам кривизны этих менисков, т. е. определяемых уравнением (III.72). Таким образом, опорожнение капилляра происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса. Так как реальные адсорбенты имеют поры раз­личных форм и размеров, которые заполняются и опорожня-

Ются при разных давлениях, то реаль­ные изотермы адсорбции имеют вид, показанный на рис. III.11. После рас­смотренного примера легко предста­вить появление гистерезиса в бутылоч­ных порах (порах с узким выходом).

Рис. II 1.11. Изотерма адсорбции при капил­лярной конденсации:

1 — кривая адсорбции: 2— кривая десорбции

Рис. 111.12. Виды пор и соответствующие им изотермы адсорбции:

А ■— конусообразная нора: 6—цилиндрическая мо­ра с одним открытым концом; в цилиндриче­ская пора с двумя открытыми концами

Капиллярно-конденсационный ги­стерезис часто обусловлен и кине­тическими причинами. Например, он может быть связан с проявлени­ем гистерезиса смачивания. Сухая поверхность с адсорбированным воздухом хуже смачивается водой (потенциальный барьер), поэтому для заполнения пор требуется давление водяного пара несколь­ко больше равновесного. При десорбции испарение пронсходіп из пор, полностью смоченных водой. Б отсутствие адсорбирп ванного воздуха угол смачивания меньше и сответственно ниже давление пара при той же степени заполнения пор (пли вели­чине адсорбции).

Капиллярная конденсация описывается уравнением Кельви на, в которое входит радиус кривизны мениска, и это позволя ет использовать его для расчета функции распределения пор по размерам. В принципе количественная характеристика дис­персных систем по дисперсности может быть представлена рас пределепием массы, объема, числа >іастиц и других параметров по радиусу, поверхности, объему, массе и др. Перейти от одно­го вида распределения к другому сравнительно просто, особен­но если поры или частицы имеют правильную форму. Метол расчета функций распределения частиц (пор) по размерам за ключается в построении интегральных и дифференциальных кривых распределения.

Для пористых тел принято характеризовать распределение пор по их радиусам, поэтому интегральная кривая распределе­ния выражает зависимость общего объема пор от их радиуса:

V’n=/(г„) (111.75)

Дифференциал от общего объема пор, или объем пор, имею­щих радиус в пределах от г„ до R„—DrH, равен

D.V„=f‘(rn)dru ІІІІ.7Г, і

Интегрированием этой функции в пределах or г„ = 0 до г„~ оо находят общий объем пор У0 в данной пробе или в единице массы пористого тела; при построении кривых распределения часто этот объем пор принимают за единицу или за 100%:

V0 = [ !'{rn)dra Или ( f'{rn)drn 1 (111.77)

О и

Если же интегрирование проводят в пределах от гп1 до г„2, то получают объем пор данной функции, или долю от общего объема, приходящуюся на эту фракцию: R—Z га

AVu^f‘(r)dr Или ( f‘(r)dr=:SVn/Ve (III. 78)

П г І

Очевидно, что чем меньше различаются пределы интегри­рования, тем ближе к истинным значениям функции распреде­ления. Как следует из соотношений (III.76) — (III.78), другой функцией распределения для данного пористого тела является зависимость /'(гп) или DV„/Dr„ от гп, которая называется диф­ференциальной кривой распределения. Она более четко и на­глядно характеризует полидисперсность системы.

Для получения кривых распределения по методу капилляр­ной конденсации используют десорбционную ветвь изотермы адсорбции (см. рис. III.11), так как для всех без исключения пор она соответствует сферическим менискам, радиусы кото­рых принимают за радиусы пор. Каждой точке кривой соот­ветствуют определенные величины адсорбции А и относитель­ного давления пара P/Ps. Зная величину адсорбции А, можно вычислить объем заполненных пор при данном давлении по уравнению, аналогичному (III.67):

V„=AVM (ІІІ.79Ї

Эффективный радиус сферического мениска г, соответству­ющий данному относительному давлению Pips, находят по уравнению Кельвина (III.72). Так как поры заполняются в Результате капиллярной конденсации после полимолекулярной адсорбции на стенках пор, то истинное значение радиуса пор гп равно сумме радиуса мениска г при полном см-ачивании и толщины адсорбционного слоя t2дс:

Гп = Г-Иадс (III.801

Величину ^адс определяют при том же давлении в отдель­ном эксперименте по адсорбции на непористых или макропори­стых адсорбентах той же природы (необходимо отсутствие ка­пиллярной конденсации) и рассчитывают по формуле

^адс —Ацп V„/Sy д (III.81)

Где Лнп — величина адсорбции на непористом адсорбенте при соответствую­щем давлении; 5уд— удельная поверхность непорнстого адсорбента.

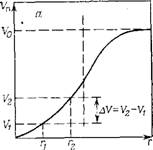
Зная Vn (III.79) и соответствующие значения Rn (III.80), строят интегральную кривую распределения (III.75), типичный вид которой представлен на рис. 111.13а. Чтобы избежать слу­чайных погрешностей, интегральную кривую «выравнивают» (т. е. усредняют) и после этого с помощью графического диф-

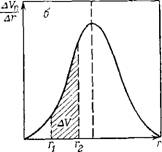
Рис. III. ІЗ. І Інтегральная (а) и дифферен­циальная (б) кривые распределения объе­ма нор по их радиусам

Ференцирования строят дифферен­циальную кривую распределения (рис. III.136). Каждая точка на интегральной кривой распределе ния, например, V{ при Гі дает объ­ем пор с радиусами от минималь­ного до Г]. По этой кривой можно определить объем пор Al/=l/2—Vi с радиусами от г, до г2 и общий объем пор V0 (рис. 111.13а).

По дифференциальной кривой распределения объем пор (или до­лю от общего объема пор), разме­ры которых лежат в пределах от г, до г2 (т. е. объем данной фрак­ции пор) определяется площадью, заключенной между осью абсцисс, дифференциальной кривой и орди­натами л и г2 (рис. 111.136). Чем резче выражен максимум н уже дифференциальная кривая, тем меньше различаются поры по размерам.

Из кривых распределения видно, что общий объем малых пор относительно небольшой. Однако доля поверхности, при­водящаяся на эти поры, существенно большая. С увеличением размера пор объем растет быстрее, чем поверхность, и в связи с этим максимум дифференциальной кривой распределения по­верхности по размерам пор сдвинут в сторону меньших радиу­сов. Построение разных кривых распределения позволяет бо­лее правильно представить структуру пористого тела, напри­мер, судить о степени полидисперсности.

Существует метод исследования и построения кривых рас­пределения, не требующий предположений относительно фор­мы пор. Этот «безмодельный» метод основан на общем тер­модинамическом соотношении, полученном А. В. Киселевым:

Andn^ods (II 1.82)

Где Ар. — изменение химического потенциала адсорбата (адсорбционный по­тенциал с обратным знаком), dn — число молей жидкости, сконденсированное в порах; ds — уменьшение поверхности адсорбента в результате заполнения пор адсорбатом.

Соотношение (111.82) показывает эквивалентность превра­щения поверхностной энергии в химическую (энергию адсорб­ции) .

Чтобы найти удельную поверхность адсорбента, необходи­мо проинтегрировать уравнение (III.82) во всей области ка­пиллярной конденсации: от максимальной поверхности (начало капиллярной конденсации) до минимальной (максимальное за­полнение пор). Так как при максимальной степени заполнения пор свободной поверхностью можно пренебречь, то поверхность s адсорбента равна:

П v-

RT

~ j ln(p/ps)]dn (III .83)

Где пк — число молей адсорбированной жидкости, отвечающее началу гисто — резисной петли.

Для построения кривых распределения пор по размерам всю область капиллярной конденсации от пк до пх разбивают на отдельные участки, которым соответствуют определенные приращения поверхности. Зная изменения An и соответствую­щие им As, можно рассчитать размеры пор и построить кривые распределения. Необходимо обратить внимание на то, что дан­ный метод не учитывает изменения поверхности, которое про­исходит до гистерезисной петли. Однако эти изменения слабо влияют на удельную поверхность и размер пор.