В разделе II. Б рассмотрены общие термодинамические соотношения, позволяющие по экспериментальным зависимостям определить основные энергетические параметры адсорбции: энергию Гиббса, энтальпию и энтропию. Модельные представления конкретизируют и упрощают анализ соотношений и расчет указанных параметров.
Между энергией Гиббса, энтальпией и энтропией адсорбции существует известное соотношение
ДО=Д# — ГД5
|
|
Самопроизвольному процессу при постоянных значениях р и Т отвечает условие AG<0. Энтропия также уменьшается при адсорбции газов и паров, т. е. А5<0, так как ограничивается свобода движения молекул: в объемной фазе они движутся в трех направлениях, а на поверхности — в двух. Из приведенного выше уравнения следует, что энтальпия адсорбции должна также уменьшаться, т. е. ДЯ<0. Таким образом, адсорбция газов и паров, как правило, — экзотермический процесс, что подтверждается экспериментально.
|
145 |
Если адсорбция подчиняется уравнениям Генри и Ленгмюра, т. е. константы равновесия адсорбции не зависят от степе
ни заполнения поверхности адсорбента, то стандартная энергия Гиббса адсорбции может быть рассчитана по уравнению изотермы Вант-Гоффа:
ДО° =— RT ]п К HI1.35)
Если К является константой Генри, то AG° характеризует переход адсорбата из стандартного состояния в объеме в стандартное состояние его на поверхности. Если же К является константой квазихимического равновесия в уравнении Ленгмюра, то AG[4] определяет химическое сродство между адсорбатом и адсорбционными центрами поверхности адсорбента в соответствии с уравнением (III.12).
Стандартную энтальпию адсорбции определяют из экспериментальной зависимости константы равновесия адсорбции от температуры в соответствии с уравнением изобары Вант — Гоффа:
ГдпК
(-ar-)o = ijfr — оп.36)
Где Д#° = #°адс—H°v — разность энтальпий адсорбата на адсорбенте и в объеме (или химической реакции).
Принимая во внимание слабую зависимость изменения энтальпии от температуры, можно провести интегрирование уравнения (III.36):
Г АН" Г 1 W J
d In К — ■ R — jidT; пК— — ~^—-f-г const (ІП-37)
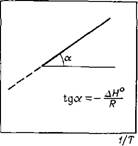
Тангенс угла наклона линейной зависимости In К-*-/Т (рис. III.8) определяет отношение —H°jR, откуда —АЯ° = — R tga. Зависимость, представленная от рис. III.8, соответствует отрицательному значению энтальпии адсорбции, что указывает на выделение теплоты в процессе адсорбции газов и паров.
Стандартную энтропию адсорбции, подчиняющейся закону Генри или уравнению Ленгмюра, легко рассчитать, если известны А//0 и AG° [см. (III.35) и (III.37) ] по уравнению:
Д + (III .38)
Поскольку уравнение Ленгмюра описывает мономолекулярную адсорбцию на однородной поверхности, то количество теплоты, выделяемое при адсорбции 1 моль вещества, постоянно и не зависит от степени заполнения. Кроме того, при мономолекулярной адсорбции дифференциальные изменения энергии Гиббса, энтальпии и энтропии совпадают с интегральными.
Стандартные энергетические параметры полимолекулярной адсорбции, соответствующие теории БЭТ, рассчитываются по
|
(II 1.39) |
|
Тем же приведенным выше уравнениям. В связи с тем, что константа С В уравнении БЭТ представляет собой отношение двух констант равновесия C=K/KL, то она также может рассматриваться как константа равновесия, т. е. для расчетов можно использовать те же изотерму и изобару Вант-Гоффа: AG°c = — RT In С=— RT In іK/KL1 |
Рис. 111.8. К определению теплового эффек — та адсорбции
|
A In С ДТ |
|
Д In (К/Кі.) ДТ |
|
АН" с RT4 ‘ |
|
(III.40) |
|
D In KL DT |
|
RT°- |
|
(III.41) |
АН с—RT2
Из уравнения (III.41) следует, что первый член в правой части отвечает полной стандартной энтальпии адсорбции, а второй — зитальпии конденсации. Таким образом, АН°с отражает стандартную энтальпию чистой адсорбции как результат взаимодействия сконденсированного пара (жидкости) с поверхностью адсорбента. Это же относится и к стандартным энергии Гиббса и энтропии чистой адсорбции.
Теория БЭТ (уравнение БЭТ) описывает адсорбцию на энергетически однородной поверхности и предполагает независимость теплоты (энтальпии) адсорбции от степени заполнения, или от числа слоев в полимолекулярном слое (одна константа конденсации). Из этого следует, что и для полимолекулярной адсорбции в теории БЭТ значения дифференциальных и интегральных термодинамических параметров совпадают (в расчете на 1 моль): К и С не зависят от степени заполнения. Так как при физической адсорбции газов и паров АН°<0, то повышение температуры ведет к уменьшению констант К и С.
|
10* |
|
147 |
При реальной полимолекулярной адсорбции по мере нарастания числа слоев константы взаимодействия уменьшаются Аі>/Сг>/Сз… (III.28), и часто требуется определить термодинамические параметры адсорбции при разных степенях заполнения. Для определения энергетических параметров полимолекулярной адсорбции по экспериментальным данным используют общий подход, рассмотренный в разд. II. Б. К тем же соотношениям можно прийти, исходя из представлений о последовательных константах адсорбции [см. уравнение (111.28)]. В общем случае адсорбционное распределение газа или пара
между поверхностным слоем и объемом можно представить в виде константы распределения [см. уравнение (III.9)]. Если принять, что адсорбатом является идеальный газ, а величина адсорбции А фиксирована, то изменением коэффициентов активности можно пренебречь, и определяемая константа распределения при данной степени заполнения адсорбента будет зависеть только от температуры. Тогда по аналогии с уравнением (III.37) можно записать:
In К= In M/p) = —АЯ°/(/?Г) + const (III.42)
Данной степени заполнения соответствует своя константа адсорбционного распределения. Так как адсорбирующийся газ принят за идеальный, то при А = const имеем:
<lnp)„ = AtfY</?r)+const (111.43)
Каждой степени заполнения адсорбента соответствует определенное значение ДН°, или определенная дифференциальная теплота адсорбции. Эта теплота адсорбции является изо — стерической, так как отвечает условию v4 = const. Как правило, она уменьшается с увеличением степени заполнения. Чтобы экспериментально определить значения этой теплоты, сначала получают изотермы адсорбции при разных температурах, затем строят график зависимости In р—у/Т (III.43) и по тангенсам углов наклона определяют изостерические теплоты адсорбции при каждой степени заполнения адсорбента. Зная АН0 и К, по уравнению (III.38) можно рассчитать также стандартную энтропию адсорбции для каждой степени заполнения адсорбента.
 2 ноября, 2012
2 ноября, 2012  admin
admin 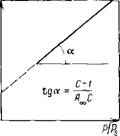
 Опубликовано в рубрике
Опубликовано в рубрике 