Под структурой тел обычно понимают пространственное взаимное расположение составных ч-астей тела: атомов, молекул, мелких частиц. Структура разбавленных агрегативно устойчивых дисперсных систем по ряду свойств очень похожа на Структуру истинных растворов. Основное отличие состоит в том, что в дисперсных (гетерогенных) системах частицы дисперсной фазы и молекулы дисперсионной среды сильно различаются по размерам. Увеличение концентрации дисперсной фазы приводит к взаимодействию ее частиц, подобному ассоциации молекул и нонов в истинных растворах. Изменение свойств дисперсных систем с ростом концентрации происходит постепенно до тех пор, пока не наступит коагуляция частиц. В коллоидной химии понятия структуры и структурообразования принято связывать именно с коагуляцией. В процессе коагуляции происходит образование пространственной структурной сетки из частиц дисперсной фазы, что резко увеличивает прочность системы.
Таким образом, структурообразование в свободнодисперс — ных системах есть результат потери их агрегативной устойчивости. По мере увеличения прочности структуры свободнодис- персная система переходит в связиодисперсную систему. Появление и характер образующихся структур, как правило, определяют по механическим свойствам систем, к важнейшим из которых относятся вязкость, упругость, пластичность, прочность. Так как этн свойства непосредственно связаны со структурой тел, то их обычно называют структурно-механическими.
Структурно-механические свойства систем исследуют методами реологии — науки о деформациях и течении материальных систем. Реология изучает механические свойства систем по проявлению деформации под действием внешних — напряжений. В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.
Термин деформация означает относительное смещение точек системы, при котором не нарушается ее сплошность. Деформацию делят на упругую и остаточную. При упругой деформации структура тела полностью восстанавливается после снятия нагрузки (напряжения); остаточная деформация необратима, изменения в системе остаются и после снятия нагрузки. Остаточная деформация, при которой не происходит разрушения тела, называется пластической.
Среди упругих деформаций различают объемные (растяжение, сжатие), сдвиговые и деформации кручения. Они характеризуются количественно относительными (безразмерными) величинами. Например, при одномерном деформировании растяжение выражается через относительное удлинение:
Y=A///O= </ — /„)//„ (VII.1)
Где 10 и I,— длина тела до и после растяжения соответственно; Д/—абсолютное удлинение.
Деформация сдвига определяется относительным сдвигом (рис. VII. 1) под действием напряжения Р:
F=t//*=tga или 1=dy/dx (VII.2)
Где у — смещение верхнего слоя; х — высота, на протяжении которой происходит смещение.
Как следует из рис. VII. 1, относительный сдвиг равен тангенсу угла сдвига а.
Жидкости и газы деформируются при наложении минимальных нагрузок. Под действием разности давлений они текут. Течение является одним из видов деформации, при котором величина деформации непрерывно увеличивается под действием постоянного давления (нагрузки). В отличие от газов жидкости при течении не сжимаются и их плотность остается практически постоянной.
Напряжение, вызывающее деформацию тела, определяется отношением силы к площади, їїа которую она действует. Действующая сила может быть разложена на две составляющие: нормальную, направленную перпендикулярно к поверхности тела, и тангенциальную (касательную), направленную по касательной к этой поверхности. Соответственно различают два вида напряжений: нормальные и тангенциальные, которым отвечают два основных вида деформации: растяжение (или сжатие) и сдвиг. Остальные виды деформации ^ожно представить с помощью различных комбинаций этих основных видов деформаций. Единицами напряжения являются в СИ Па (паскаль), в системе СГС — дин/см2.
Соответствие Характера деформации виду напряжения подтверждает первая аксиома реологии: при всестороннем равномерном (изотропном) сжатии все материальные системы ведут себя одинаково — как идеальные упругие тела. Это означает, что в таких разных по структуре телах, как металл, смола, вода, кислород (газ), изотропное сжатие вызывает только упругую деформацию, а именно, уменьшаются размеры системы при сохранении ее формы и увеличивается плотность. При снятии нагрузки все параметры тела принимают первоначальные значения. Отсюда следует, что изотропное сжатие не позволяет выявить качественные различия в структуре тел.
|
|
|
I / Рис. VI 1.1. Схематическое изображение де — * ,сС/ формации сдвига |
Вместе с" тем любая материальная система обладает всеми реологическими свойствами (Вторая аксиома реологии). Основными из них, как уже упоминалось, являются упругость, пластичность, вязкость и прочность. Все эти свойства проявляются при сдвиговой деформации, которая поэтому считается наиболее важной в реологических исследованиях.
|
|
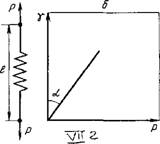
Рис. VII.2. Модель идеального упругого тела Гука (а) и зависимость деформации этого тела от напряжения (б)
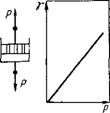
Рис. VI 1.3. Модель идеально вязкой жидкости Ньютона (а) и зависимость скорости деформации этой жидкости от напряжения (б)
Таким образом, характер и величина деформации зависят от свойств материала тела, его формы и способа приложения внешних сил.
В реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона.
Идеально упругое тело Гука представляют в виде спиральной пружины (рис. VI 1.2). В соответствии с законом Гука деформация в упругом теле пропорциональна напряжению сдвига
Р-
1—Р/Е или Р=Еч (VII.3)
Где Е — коэффициент пропорциональности, или модуль Юнга.
|
|
Модуль Юига Е является характеристикой материала (его структуры), количественно отражающей его упругие свойства (жесткость). Из уравнения (VII.3) следует, что единицами модуля Юнга являются паскаль (СИ) и дин/см2 (СГС), т. е. те же, что и для напряжения, так как величина у безразмерна. Модуль Юнга можно определить по тангенсу угла наклона а прямой, характеризующей зависимость деформации у от напряжения (см. рис. VII.2, б). Модуль упругости составляет для молекулярных кристаллов ~109 Па, для ковалентных кристаллов и металлов — 10й Па и более. После снятия нагрузки идеально упругое тело Гука мгновенно переходит в первоначальное состояние (форму). Принято, что для упругих тел этот пе
реход происходит со скоростью, не меньшей скорости распространения звука в них.
Идеально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью (рис. VII.3). Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью т] пропорционально градиенту ее скорости Du/Dx:
P=idu/dx (VII.4)
При плоскопараллельном движении двух слоев жидкости происходит сдвиг одного слоя относительно другого. Если ско-‘ рость движения слоев жидкости обозначить через Dyjdr И учесть, что координата х и время т являются независимыми переменными, то с помощью изменения порядка дифференцирования можно получить следующее соотношение:
Du/dx=d1y/idxdx)^d-i/dx= (VII.5)
Где — скорость деформации сдвига.
Таким образом, закон Ньютона можно сформулировать еще следующим образом: напряжение сдвига пропорционально скорости деформации (или скорость деформации пропорциональна напряжению сдвига)
•Р=»П (VII.6)
Реологические свойства идеальных жидкостей однозначно характеризуются вязкостью. Ее определение дается уравнениями
(VII.4) и (VII.6). График зависимости Р-*-^ представляет собой прямую, выходящую из начала координат, тангенс угла
Наклона этой прямой к оси ^ определяет вязкость жидкости, а к оси Р — величину, обратную вязкости, называемую текучестью. Если вязкость характеризует сопротивление жидкости движению, то текучесть — ее подвижность. Единицы вязкости следуют из уравнения (VI 1.6). Так как в международной системе единиц напряжение измеряется в Паскалях, а скорость деформации в с-1, то единицей вязкости будет паскаль-секунда (Па-с). В системе СГС за единицу вязкости принят пуаз (П) (1Па-с=10П). Вязкость воды при 20,5°С равна 0,001 Па с или 0,01 П, т. е. 1 сантипуазу (сП). Вязкость газов примерно в 50 раз меньше, у высоковязких жидкостей значения вязкости могут достигать в тысячу и миллионы раз больше, а у твердых тел она может составлять 1015—1020 Па-с и более. Размерность текучести обратна размерности вязкости, следовательно, единицы вязкости обратны единицам текучести. Например, в системе СГС текучесть измеряется в пуазах в минус первой
Степени (П-1). Иногда эта единица называется и обозначается «ре».
Величина деформации жидкости зависит от времени действия напряжения. Так как
Ч=Р/Л или d^/dx=Р/ц Р
V =— т V Л
Т. е. деформация при постоянном напряжении Р пропорциональна времени действия этого напряжения. Идеальные жидкости способны течь (деформироваться) под действием очень малых внешних нагрузок до тех пор, пока они действуют.
|
(VI 1.8)’ |
|
(VII.9) |
Моделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы (рис. VII.4). В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т. е. при
Р <Рт Ї=0 и 1=0
Если напряжение достигнет предела текучести, то развиваемая деформация идеально пластического тела не имеет предела, и течение происходит с любой скоростью, т. е. при
/>=/>т 1 > О и 1 > О
Эта зависимость показана на рис. VII.4, б. Из нее следует, что к элементу сухого трения (идеально пластическому телу) не может быть приложено напряжение, превышающее Рг. Величина Рг отражает прочность структуры тела. При условии Р — Рт структура идеального пластического тела разрушается, после чего сопротивление напряжению полностью отсутствует.
|
|
Сравнение идеальных элементов (реологических моделей) показывает, что энергия, затраченная на деформацию упругого тела Гука, возвращается при разгрузке (после прекращения действия напряжения), а при деформа — Q ции вязкого и пластического тел энергия превращается в теплоту. В соответствии с этим тело Гука принадлежит
К КонсерватиВныМ системам, а другиЕ два^- к диссипативным (теряющим энер — г ню) ————— —————
Рис. VII.4. Модель идеально пластического тела Сеи-Венаиа — Кулона (а) н зависимость деформации этого тела от напряжения (б)
 2 ноября, 2012
2 ноября, 2012  admin
admin 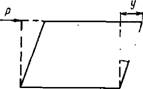

 Опубликовано в рубрике
Опубликовано в рубрике 