Лако-красочные материалы — производство

Широкий спектр структурно-механических свойств отражает многообразие природных и синтетических тел, большинство из которых является дисперсными системами со всевозможной комбинацией фаз, различающихся природой и агрегатным со­стоянием, размером частиц и взаимодействиями между ними. Поэтому структурно-механические свойства дисперсных систем представляются непрерывным и бесконечным рядом не только промежуточных, аддитивно складываемых свойств, но и каче­ственно новых, не присущих отдельным компонентам. Умение управлять процессами, протекающими в дисперсных системах, открывает неограниченные возможности для получения матери­алов с заданными свойствами.

Благодаря, главным образом, работам П. А. Ребиндера, и его учеников учение о структурообразовании превратилось в теоретические основы синтеза материалов — самостоятельный раздел коллоидной химии, названный физико-химической ме­ханикой. *

Анализ многообразных свойств структур в дисперсных сис­темах позволил П. А. Ребиндеру разделить их на два основных класса, различающихся по видам взаимодействия частиц дис­персной фазы. Исходя из того, что коагуляция соответствует первичному и вторичному минимуму потенциальной кривой взаимодействия частиц, он предложил различать конденсаци- онно-кристаллизационные и коагуляционные структуры. Кон- денсационно-кристаллизационное структурообразование, отве­чающее коагуляции в первичном потенциальном минимуме, осуществляется путем непосредственного химического взаимо­действия между частинами и их срастания с образованием жесткой объемной структуры. Если частицы аморфные, то структуры, образующиеся в дисперсных системах, принято называть конденсационными, если частицы кристаллические, то структуры являются кристаллизационными. При непосредст­венном срастании частиц механические свойства структур соот­ветствуют свойствам самих частиц. Конденсационно-кристалли — зационные структуры типичны для связнодисперсных систем, т. е. систем с твердой дисперсионной средой. Такие структуры придают телам прочность, хрупкость и не восстанавливаются после разрушения.

Под коагуляционными структурами понимают структуры, которые образуются при коагуляции, соответствующей вторич­ному минимуму потенциальной кривой взаимодействия частиц дисперсной фазы (хотя конденсационно-кристаллизацио’нные структуры также формируются в результате коагуляции). При образовании коагуляционных структур взаимодействие частиц, осуществляемое через прослойки дисперсионной среды, явля­ется, как правило, ван-дер-ваальсовым, и поэтому — пространст­венный каркас такой структуры не может отличаться высокой прочностью. Механические свойства коагуляционных структур определяются не столько свойствами частиц, образующих структуру, сколько характером и особенностями межчастичных связей и прослоек среды; Коагуляционные " структуры имеют обычно жидкую дисперсионную среду. Для них характерна способность восстанавливать структуру во времени после ее механического разрушения. Это явление получило название Тиксдтропии. Соответственно подобные структуры часто еще называют коагуляционно-тиксотропными.

Самопроизвольное восстановление коагуляционной структу­ры свидетельствует о том, что она обладает наибольшей меха­нической прочностью при относительном минимуме энергии Гиббса. Такое соответствие отсутствует у конденсационно-кри — сталлизационных структур, которые образуются обычно в ус­ловиях высоких пересыщений и поэтому термодинамически не­устойчивы. Их высокая прочность обеспечивается одновремен­ным уменьшением пересыщения и снижением внутренних напряжений.

В практической деятельности люди используют реальные тела с разнообразной структурой. Как правило, материалы и изделия из них являются твердыми телами, имеющими конден- сационно-кристаллизационные структуры (металлы, сплавы, керамика, бетон и др.), а сырье и промежуточные продукты чаще всего представляют собой жидкообразные или твердооб — разные системы с коагуляционной структурой. Последние очень удобны в технологии материалов, поскольку обеспечивают воз­можность регулирования состава и однородности, а в техно-

Р рт р Рис. VII.8. Типичные кривые течения жидкообразиых тел:

/ — ньютоновские жидкости; 2— псевдопластические жидкости; 3— дилатантные жид­кости

Рис. VII.9. Типичные кривые течения твердообразных тел:

1 — бингамовское тело; 2 — псевдопластическое твердообразное тело; 3 — пластическое днлатантное тело

Логии изделий — регулирование процессов формования и др.. В процессе изготовления материалов и изделий из них, как правило, осуществляется переход от коагуляционных структур к конденсационно-кристаллизационным.

Разнообразие структур в реальных дисперсных системах не позволяет четко разделить их на два указанных вида. Безус­ловно, существует множество промежуточных состояний систем. И все же предложенная П. А. Ребиндером классификация структур дисперсных систем помогает связать механические свойства тел с их строением.

Имеются классификации тел, основанные на их реологиче­ских свойствах. В соответствии с этими свойствами все реаль­ные тела принято делить на жидкообразные (предел текучести равен нулю, Рт = 0) и твердообразные. (РтХ)).

Жидкообразные тел’а классифицируют на ньютоновские и Неньютоновские жидкости. Ньютоновскими жидкостями называ­ют системы, вязкость которых не зависит от напряжения сдви­га и является постоянной величиной в соответствии с законом Ньютона. Течение неньютоновских жидкостей не следует зако­ну Ньютона, их вязкость зависит от напряжения сдвига. В свою очередь, они подразделяются на стационарные, .реоло­гические свойства которых не изменяются со временем, и не­стационарные, для которых эти характеристики зависят от вре­мени. Среди неньютоиовских стационарных жидкостей разли­чают псевдопластические и дилатантные. Типичные зависимо­сти скорости деформации жидкообразиых тел от напряжения (кривые течения, или реологические кривые) представлены на рис. VII.8.

Экспериментальные исследования показали, что графические зависимости между напряжением сдвига и скоростью деформа­ции, представленные в логарифмических координатах, для ста­ционарных жидкообразиых систем часто оказываются линей-
иыми и различаются только тангенсом угла наклона прямой. Поэтому общую зависимость напряжения сдвига от скорости деформации можно выразить в виде степенной функции:

<VII.24>

Где K и п — постоянные, характеризующие данную жидкообразиую систему.

Двухпараметрическое уравнение (VII.24) известно под наз­ванием математической модели Оствальда — Вейля. Ньютонов­ская вязкость tj неиьютоновской стационарной жидкости опре­деляется уравнением

(VII.25)

Если п=1, жидкость является ньютоновской и константа k совпадает со значением ньютоновской вязкости (кривая I на рис. VII.8). Таким образом, отклонение п от единицы ха­рактеризует степень отклонения свойств жидкости от ньюто­новских. Для псевдопластических жидкостей (п< 1) характер­но снижение ньютоновской вязкости с ростом скорости дефор­мации сдвига (кривая 2 на рис. VII.8). Для дилатантных жид­костей л>1 и ньютоновская вязкость растет с увеличением скорости деформации сдвига (кривая 3 на рис. VII.8).

Разбавленные дисперсные системы с ровноосными частица­ми обычно представляют собой ньютоновские жидкости. К псев­допластическим жидкостям относятся суспензии, содержащие асимметричные частицы, и растворы полимеров, например про­изводные целлюлозы. По мере роста напряжения сдвига час­тицы суспензии постепенно ориентируются своими большими осями вдоль направления потока. Хаотическое движение час­тиц меняется на упорядоченное, что ведет к уменьшению вяз­кости. Дилатаитные жидкости в химической технологии встре­чаются редко, их свойства характерны, например, для некото­рых керамических масс. Дилатантное поведение наблюдается у дисперсных систем с большим содержанием твердой фазы* При течении таких дисперсных систем под действием малых нагрузок дисперсионная среда играет роль смазки, уменьшая силу^ трения и соответственно вязкость. С возрастанием нагруз­ки плотная упаковка частиц нарушается (разрыхляется), объ­ем системы несколько увеличивается (увеличивается межчас- тичиый объем),, что приводит к оттоку жидкости в расширен­ные участки и недостатку ее для смазки трущихся друг о друга частиц, т. е. вязкость возрастает.

Твердообразные дисперсные системы подразделяют на бин — гамовские и небингамовские. Их поведение описывается общим уравнением:

P — Pt-kf

При п= 1 уравнению следует бингамовское тело, п> 1 — пластическое дилатантное тело и п< 1 — псевдопластическое твердообразное тело (рис. VII.9).

Необходимо отметить, что твердообразные и жидкообразные тела отличаются не только наличием или отсутствием предела текучести, но и определенным поведением при развитии дефор­мации. Для СтруктуРирОванных нагрузки характерен переход к Ньютоновскому течению, отвЁыагевдему

Npeflg лЬно-разрушетт^^ ре; для твердОрЛразных телуво——-

Личение нагрузки"Приводит К рязрьшу^длошногти тела, и его — отзрущіешш: Имеется множество систем, обладающих проме­жуточными структурно-механическими свойствами.

По реологическим свойствам к бингамовским твердообраз — ным системам очень близки Пульпы, ш л амы, буро вы е — растдо — ры, масляные краски, зубные пасты д ‘тід — Они отличаются би Л ьш и м‘ТфеДел&м^геКуч ести^’ а при развитии деформации ве­дут себя как структурированные жидкости. Такие системы часто относят к неньютоновским жидкостям.

Для типичных твердообразных тел характерен значитель­ный предел текучести. Хрупкое тело разрушается при на­грузке, меньшей предела текучести (предела упругости). В болынидств^ реальных тверлых, тел. пластическиедеформа — Ции развиВаются при всех НагрузКах, но часто в области малых.,- ^нагрузоїГТттгтшжно-прєнеоречьТТЗ соответствии с этиМ предел текучесТи в ТОЙ ИЛИ ИНОЙ степени является УСЛОВНЫМ— Если ОщуП. кое~ТёЗю подвергнуть Всестороннему сжатию прИ йЫсоких Давлениях и предотвратить возможность его разрушения, то при ДостаточнО высокиХ напряжениях оно можрт рроДдлятк пластичность^""?. е. необратимо деформироваться без потери сплошности!"*

Таким образом, деление твердых тел на упругие, пластич­ные и хрупкие также до известной степени условно, так как характер деформации зависит от условий, типа напряжений, продолжительности их действия и других факторов. К хруп­ким твердообразиым телам можно отнести неорганические материалы типа бетонов, керамики на основе различных окси­дов и др. Металлы и сплавы обладают пластическими свойст­вами. Высокоэластическое и вязкотекучее состояния более ха­рактерны для органических пластиков.

Для нестационарных систем, реологические свойства кото­рых изменяются со временем, характерны явления тиксотропии и реопексии. Тиксотропия — специфическое свойство коагуля — ционных структур. Разрушение структуры выражается в раз­рыве контактов между частицами дисперсной фазы, а ее je»k—- се^Юпное восст^новлР"1^ — в Возобновлении этих контактов .. В с л Є Д CT вне ПОД В И Ж Н о С т И среДы И броуновского движения чяг — ™Ц — Восстановление гТрук туры._о. бй. чно контролируется по уве — —L.Рис. VII.10. Обнаружение тиксотропии по кри-

‘ 1вым течения:

/ — равновесная кривая; 2 — неравновесная кривая

Личению вязкостИ системы, поэТому яв­ление тиксотропии можно определить ‘кагуИёньшение вязкости „системы во ВрШенїГпвяи. далажении нагрузки и по­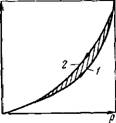 Степенный рост вязкости после снятия иа’Грузки. Явление тиксотропии соответ­ствует поведению псе В д ОЇЇлї стйч ее ких тел, у них вязкость уменьшается с ростом напряжения сдвига. Чем медленнее вос-

Или чем медленнее она разрушается (уменьшается вязкость) при данном напряжении сдвига, тем сильнее выражено явление тиксотропии.

На рис. VII. 10 представлены кривые течения системы, обла­дающей тиксотропией. Кривая / отражает равновесную зави­симость, ее получают при увеличении напряжения сдвига. За­висимость, соответствующую кривой 2, получают при снижении нагрузки, когда еще не успело установиться равновесие между прочностью структуры и напряжением сдвига. Расстояние меж­ду двумя кривыми по оси напряжений, или площадь петли, характеризуют степень тиксотропности. Если обратимое восста­новление структуры происходит очень быстро, то тело можно отнести к стационарным псевдопластическим; иногда говорят, что оно обладает мгновенной тиксотропией.

Более строгий метод количественной оценки тиксотропиых свойств основан на эмпирическом уравнении:

(VII.27)

Где А, В и С — константы, В — показатель псевдопластичности; С — показа­тель тиксотропиых свойств.

Увеличение константы В означает, что жидкообразное тело становится более восприимчивым к деформации, а увеличение С показывает, что его свойства становятся в большей степени зависимыми от времени. Для определения констант проводят соответствующие экспериментальные испытания.

Ярко выраженной тиксотропией обладают суспензии бенто­нитовой глины с концентрацией дисперсной фазы более 10%. В спокойном состоянии эта система представляет собой пла­стическое твердообразное тело, которое не течет под действием силы тяжести. После встряхивания суспензия настолько разжи­жается. что может легко вытекать из сосуда. Через определен­ное время выдерживания суспензии в спокойном состоянии она снова превращается в нетекучую структурированную сис­тему. Явление тиксотропии проявляется в природе при образо­вании плывунов, оползней. Его необходимо учитывать при пе­рекачке суспензий, которые могут затвердевать при возможной остановке насосов.

Вместе с тем тиксотропия способствует более эффективному проведению ряда технологических операций. Например, тиксо­тропия позволяет проводить вибрационную обработку матери­алов, при которой происходит разрушение структуры, что об­легчает процессы перемешивания, обеспечивает плотную упа­ковку, снятие внутренних напряжений и т. д.

К явлению, противоположному тиксотропии, относится ре — опексия. Реотксия — возрастание прочности структуры — вяз­кости) со временем при действии НапряЖения сдвига^-Напри — мер, после тиксотропного разжижения гидрозоля восстановлен нйеіструктуры может происходить значительно быстрее, если медленно перемешивать систему. Это явление обычно наблю­дается в гидрозолях с частицами палочкообразной формы, поэтому существует мнение, что небольшое увеличение течения способствует параллельной ориентации частиц и соответствен­но ускорению образования структуры.