Поверхностно-активные вещества (ПАВ), молекулы которых имеют дифильное строение и включают большой углеводородный радикал, отличаются высокой поверхностной активностью по отношению к воде, что отражает сильную зависимость поверхностного натяжения водного раствора ПАВ от их концентрации. Большие значения поверхностной активности предполагают пренебрежимо малые концентрации ПАВ в объеме раствора по сравнению с концентрацией их в поверхностном слое, т. е. с величиной их адсорбции на границе раствор — воздух. Подобная зависимость может обнаруживаться и в растворах других веществ на границе с жидкостью или твердым телом, например при специфическом взаимодействии с поверхностью. Отмеченная особенность позволяет пренебречь разницей между величиной адсорбции А и величиной гиббсовской адсорбции Г, т. е. Из этого соотношения следует, что
Для растворов ПАВ все уравнения адсорбции, включающие величину адсорбции А, будут также справедливы, если заменить А на Г. Одним из таких уравнений является выражение закона Генри, который характеризует адсорбцию при малых концентрациях.
Применительно к адсорбции неионогенных (недиссоцииру- ющих) ПАВ закон Генри запишется так:
Л = Г=/чгс (III.119)
В такой записи закон Геирп можно сопоставить с адсорбционным уравнением Гиббса (11.71):
А=*Ге=Кгс=*J" (III.120).
|
|
Рис. III.19. Изотермы адсорбции и поверхностного натяжения для растворов ПАВ в области действия закона Генри
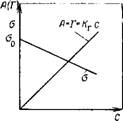
Рис. 111.20. Изотермы адсорбции и поверхностного натяжения для растворов ПАВ в области действия изотермы Ленгмюра
Разделим переменные и проведем интегрирование уравнения (III. 120) в пределах от Оо (поверхностное натяжение чистого растворителя) до о и соответственно от с = 0 до с:
А с
F da = — f KtRT dc
Во о
После интегрирования получим
О = о0 — KrRTc (III.121)
Таким образом, в области действия закона Генри поверхностное натяжение линейно уменьшается с увеличением концентрации неионогенного ПАВ (рис. III.19). Тангенс угла наклона прямой A = F(C) определяет поверхностную активность (с обратным знаком), а из уравнений (III.120) — (III.121) следует, что
G=—{do/dc)c^ = RTKr (III.122)
Т. е. поверхностная активность ПАВ пропорциональна константе распределения Генри.
При увеличении концентрации ПАВ закон Генри перестает соблюдаться и поэтому необходимо обратиться к уравнению изотермы адсорбции с константой обмена К (III. 105). Если выразить молярную долю ПАВ в поверхностном слое х через величину адсорбции А, получим:
1 + <кХ-і)Х <ШЛ23)
|
|
Принимая во внимание большую поверхностную активность ПАВ (/С3>1) и пропорциональность молярных долей моляр — ностям при малых концентрациях, получим, что адсорбция неионогенного ПАВ следует уравнению Ленгмюра. Учитывая так
же соотношение Г «Л, величину адсорбции можно приравнять к ее выражению, соответствующему уравнению Гиббса
Кс с do
Л = Л. ТТЛГ — —RT-dT <1,,Л24>
После разделения переменных имеем:
Kdc
-do = ART
Kc Или
Ос с
— J do « A^RT f AXRT J d In ( 1 + Kc)
A„ о 0
Так как d (1 = Kdc.
После интегрирования получим уравнение Шишковского, характеризующее поверхностное натяжение растворов ПАВ в зависимости от концентрации:
А = а0 — А^Т In (1+/Сс) (I1I.125>
Подобную зависимость о от с для ПАВ Б. А. Шишковский получил опытным путем. Ленгмюр, связав уравнение Гиббса со своим уравнением, определил физический смысл констант эмпирического уравнения Шишковского. Одна из них равна произведению AXRT, другая константа Д имеет смысл константы адсорбционного равновесия в уравнении Ленгмюра (или константы обмена). Допущения, принятые при выводе уравнения Шишковского, показывают, что это уравнение в отличие от уравнений Гнббса и Ленгмюра справедливо только для по — верхностно-активных веществ, обладающих высокой поверхностной активностью.
Зависимость поверхностного натяженния растворов ПАВ от их концентрации в соответствии с уравнением Шишковского показана на рис. III.20. Из рис. III.20 видно, что при малых концентрациях ПАВ в растворе поверхностное натяжение снижается резко, но с ростом концентрации степень его снижения уменьшается и о стремится к постоянному значению. Из вывода уравнения Шишковского следует, что такой ход зависимости о от с обусловлен теми же причинами, что и снижение прироста адсорбции, а именно уменьшением концентрации свободных от ПАВ адсорбционных центров. Уравнение Шишковского, как и уравнение Ленгмюра, не учитывает взаимодействия молекул ПАВ на поверхности.
Ю. Г. Фроловым были проанализированы особенности изотерм адсорбции и поверхностного натяжения для растворов ионогенных ПАВ и получены соответствующие уравнения. Эти особенности обусловлены протеканием диссоциации ионогенных
ПАВ в объеме, например водного раствора, и отсутствием диссоциации (или значительном уменьшении) в поверхностном слое, так как смежная фаза обычно неполярна. Проводя вывод уравнения концентрационной зависимости адсорбции ионогенных ПАВ аналогично выводам закона Генри и уравнения Ленгмюра и используя при этом выражение для актив — — ности электролитов (ПАВ), представленное через средние ионные-концентрации с±, получим следующие изотермы адсорбции ионогенных ПАВ:
А = КтС± (III.126)
Кс
(ШЛ27)
Где v=v+ + v_ — стехнометрические коэффициенты соответственно катиона и аниоиа в формуле электролита.
Выводы, аналогичные выводам соотношений (III.121) и (III.125) приводят к следующим изотермам поверхностного натяжения растворов ионогенных ПАВ в соответствующих областях концентраций:
О=сг0— KTRTC"± (III.128)
О=Оо — Л«ЯГ1п (1+ЛГсМ (III.129)
Особенности изотермы адсорбции ионогенных ПАВ, вытекающие из уравнений (III.126) —(III.127), иллюстрируются на рис. III.21. Во-первых, в области малых концентраций (с-*-0) изотерма адсорбции представляет собой параболу, а коэффициент распределения ионогенного ПАВ при с-Я) стремится к нулю [D = A/C = Kc±V~1, см. уравнение (III.126)], а не к постоянной величине, как это следует для неэлектролитов из закона Генри. Во-вторых, изотерма адсорбции имеет перегиб при значении концентрации, вблизи которого кривая коэффициента распределения ионогенного ПАВ проходит через максимум.
Закономерности адсорбции ионогенных ПАВ соответствующим образом отражаются и на особенностях изотермы поверхностного натяжения их растворов (см. рис. 111.21). Изотерма о(с) при малых концентрациях, в отличие от изотермы для растворов неионогенных ПАВ, представляет собой параболу (III.128); с увеличением концентрации обнаруживается перегиб в соответствии с уравнением (III. 129).
Из определения поверхностной активности ионогенных ПАВ (11.77), являющегося наиболее общим (для неионогенных ПАВ v=l), следует ее пропорциональность константе распределения (III.128):
G±=— (da/de±)c »о= KrRT ШІ.130»
Зависимость производной, определяющей поверхностную активность, от концентрации в более общем виде можно получить из соотношения (III.129):
Da d In (l+Kcl)
-RTAa
Del. °° del
Обозначим 1-)-Kc^’ — y, тогда Dy = Kdc±
|
± |
|
(111.131) |
Dln( + KcU Kd In У К К
Del dy ‘ У 1 4- Kc
Таким образом
Da RTA^K RTKr
Del 1 + Kcl 1 + Kc±
Для неионогенных ПАВ v=l.
Дальнейшее увеличение концентрации как ионогенных, так и неионогенных ПАВ с большой поверхностной активностью (выше растворимости) может привести к появлению мицелл в растворе и на межфазной поверхности, что равнозначно возникновению новой фазы (механизм образования мицелл ПАВ рассматривается в разд. VLB, посвященном растворам коллоидных ПАВ). Поэтому закономерность изменения величины адсорбции с увеличением концентрации ПАВ меняется.
 2 ноября, 2012
2 ноября, 2012  admin
admin 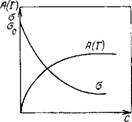
 Опубликовано в рубрике
Опубликовано в рубрике 