При рассмотрении адсорбции газов и паров на твердых адсорбентах допускалось, что до адсорбции поверхность адсорбента свободна от молекул адсорбата и она постепенно заполняется адсорбатом с ростом давления в соответствии с изотермой адсорбции. При адсорбции из жидких растворов поверхность адсорбента всегда полностью занята молекулами растворителя И растворенного вещества. Растворенное вещество может адсорбироваться только вытесняя из поверхностного слоя молекулы растворителя, т. е. происходит обменная молекулярная адсорбция. Таким образом, в адсорбции из растворов участвуют как минимум два адсорбирующихся компонента. Применительно к молекулярной адсорбции из бинарного раствора фундаментальное адсорбционное уравнение Гиббса (11.63) принимает вид
— с/а = Г, й(1, + Г2йц2 (111.92)
Где Гі и Г2—величина гиббсовской адсорбции компонентов / (растворитель) и 2 (растворенное вещество) соответственно.
Чтобы связать величины гиббсовской адсорбции с концентрациями компонентов в растворе, используем уравнение Гиббса — Дюгема:
Л-,</ц, + л-2с/ц2=0 (111.93*
Где Xt и х2 — молярные доли компонентов 1 п 2 в растворе. Выражение концентраций в молярных долях удобно для описания обменной адсорбции, так как позволяет выразить концентрацию одного компонента через концентрацию другого.
Из уравнения (III.93) найдем выражение для dfii, которое затем подставим в уравнение (III.92):
— da= (Г2 — ґ|.ї2/.ї,)гіц2 (111.94)
Для получения зависимости Г2 от, v2 (изотермы) допустим, что общее число молей компонентов / и 2 в поверхностном слое до и после адсорбции остается одним и тем же. Тогда при адсорбции добавление одного компонента в поверхностном слое будет равно убыли другого компонента, следовательно, Г2 = = —Гь Подставляя это соотношение в уравнение (III.94) и Учитывая, что. v,-}-,v2=l, получим:
Г2 — — U —x2)da/dvL2 U1
Выразив химический потенциал p2 через активность компонента а2, можно записать
A., da
Г, (III.96)
Уравнения (III.95) и (111.96) аналогичны уравнению Гиббса для адсорбции из разбавленных растворов (11.71), однако они отражают более общую зависимость и справедливы для всей области концентраций. Если концентрация второго компонента (растворенного вещества) стремится к нулю, то эти уравнения переходят в уравнение Гиббса для разбавленных растворов. Для практического использования уравнений (II 1.95) и (III.96) необходимо знать или предварительно определить активности компонентов в растворах и межфазное натяжение. Несмотря на то, что эти уравнения справедливы для адсорбции из растворов на любой границе раздела, их используют обычно для описания адсорбции в системах жидкость — газ и жидкость— жидкость, что связано с возможностью определения межфазного натяжения. Однако анализ этих уравнений позволяет получить общее представление об изменении гиббсовской
адсорбции компонентов в зависимости от состава раствора и на границе с твердым телом.
Типичные зависимости гиббсовской адсорбции от состава бинарного раствора представлены на рис. III. 15. В соответствии с уравнением (III.96) гиббсовская адсорбция компонента 2 при всех его концентрациях положительна, если с увеличением концентрации межфазное натяжение уменьшается. При этом условии зависимость Г2 от состава раствора имеет максимум [кривая Г2 (Л)]- Максимум обусловлен главным образом тем, что величина адсорбции Г2 пропорциональна произведению Л|Х2 (так как 1—л’2 = *і н а2 = х2^, где j2— коэффициент активности компонента 2), а максимум функции г/ = л’,х2=(1—Х2)х2 = ~Х2—л’і2 отвечает условию dy/dx=—2.ї2 = 0 или х = х2 = 0,5. Изменение величин а и ], входящих в уравнение (III.96), с изменением состава раствора влияет на координаты максимума.
Если компоненты бинарного раствора имеют близкие значения поверхностной активности, то возможно изменение знака величины гиббсовской адсорбции с изменением состава раствора, что соответствует пересечению изотермы адсорбции с осью составов [кривая Г2 (2)]. Точка пересечения отвечает такому состоянию системы, при котором составы раствора и поверхностного слоя одинаковы. Это значит, что компоненты раствора не могут быть разделены с помощью данного адсорбента. Такое явление получило название адсорбционной азео — тропии. Очевидно, что для компонента 1 зависимость Гі от хх Будет симметрична зависимости Г2 от х2 относительно оси составов, так как при данном адсорбенте, если второй компонент поверхностно-активен по отношению к первому, то первый — поверхностно-инактивен по отношению ко второму. Кроме того, предполагается (сделано допущение), что приращение в поверхностном слое одного компонента равно убыли другого.
|
|
|
Рис. III.15. Зависимость гиббсовской адсорбции от состава бинарного раствора: Х=1 Tj (I) и Гі (1) соответственно положительная н отрицательная адсорбция компонентов бинарного раствора, Г| (2) н Г2 (2) — иллюстрация а дсорбционной азеотро- пии |
Наглядную зависимость величины гиббсовской адсорбции от состава раствора можно получить, рассматривая баланс перераспределения компонентов между объемом и поверхностным слоем. Обозначим через п0 общее число молей в системе, из которых nv — число молей в объеме, ns — число молей в поверхностном слое, П — число молей компонента 1 и л2 — число молей компонента 2 в объеме после адсорбции, и А2 — чис-
до молей соответственно компонентов 1 и 2, приходящихся на единицу площади поверхностного слоя (площадью s). Тогда общее число молей обоих компонентов в системе составит
П0 — п^ +ns = n,+n2 + Als + A2s (111.97)
Молярные доли компонента 2 до и после адсорбции равны:
Лг02= (п2 +A^s) / па х2=:пгЦпх—піі (III.98)
Используя соотношения (III.98), запишем выражение для величины гиббсовской адсорбции компонента 2 (11.49). Именно этот гиббсовский избыток получается при расчете величины адсорбции по разности количеств вещества в объеме до и после адсорбции:
Г "О(*Р2 — *■■>) . "о("і"2 + П* -VjS 4- A2n2s — П2П0) I lC= s ^ (ІП.99)
|
Г4, |
Подставив вместо n0 (в скобках) его выражение (III.97), получим
П|П2 + л22 + Лої і s 4- /l2n2s — njfi2 — л22 — <4іП25 ■
("j + «2)s
A.,nx — Atn2
A2x^ A X2
■-і і —г
Или Г2 = А2Хі — А,х2 (111.100)
Соотношение (III. 100) также описывает зависимости, представленные на рис. III. 15. Для удобства его анализа умножим и разделим правую часть уравнения на х, л’2:
Г2—Х, х2(А2/Х2— А/х) (III. 101)
Отношения А!х и А2ІХ2 характеризуют коэффициенты расг пределения компонентов между поверхностным слоем и объемом раствора. Если при всех составах раствора A2/x2>Alxu то Гг>0, а произведение xtx2 объясняет наличие максимума [кривая Гг (Л]- Если в системе возможно увеличение коэффициента распределения компонента 1 при изменении состава раствора, то изотерма адсорбции пересекает ось составов [кривая Г2 (2)] в точке, соответствующей равенству А/х^=А2/х2. Из соотношения (III.101) следует симметричность изотермы адсорбции компонента 1 по отношению к изотерме адсорбции компонента 2.
 2 ноября, 2012
2 ноября, 2012  admin
admin 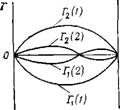
 Опубликовано в рубрике
Опубликовано в рубрике 