Межфазные поверхности могут существовать только при наличии в системе жидкой или твердой фазы. Именно эти фазы определяют форму и строение поверхностного слоя — переходной области от одной фазы к другой. Свойства поверхностного слоя непосредственно связаны с объемной структурой жидких и твердых фаз. К этому факту мы будем обращаться и в дальнейшем, а здесь отметим существенное влияние на свойства поверхностей жидких и твердых тел большой подвижности молекул жидкости и практической неподвижности молекул и атомов твердого тела.
Поверхностный слой жидкости вследствие подвижности молекул в объеме, а также в результате постоянно протекающих процессов испарения и конденсации находится в состоянии непрерывного обновления. Так, среднее время жизни молекулы воды на поверхности составляет около 10~7 с. Плотность граничного слоя между водной фазой и ее насыщенным паром изменяется непрерывно от плотности жидкой воды до плотности ее пара. Обычно толщина поверхностного слоя жидкости существенно зависит от температуры. В то же время межмолекуляр — ные силы обеспечивают наличие поверхностного слоя жидкости определенной толщины. Чем больше межмолекулярные силы, тем на меньшее расстояние молекулы могут диффундировать с поверхности, т. е. тем меньше толщина поверхностного слоя. Внутренняя граница слоя соответствует началу изменения структуры жидкости в объеме. Вследствие подвижности жидкости имеют гладкие и сплошные, или эквипотенциальные, поверхности, т. е. с термодинамических позиций (макросостояния) все точки поверхности жидкости энергетически эквивалентны.
Поверхность твердого тела в отличие от поверхности жидкости в течение долгого времени может оставаться такой же, какой она была в момент образования. Вместе с тем многие твердые тела обладают пластическими свойствами и при определенных условиях могут течь. Таким образом, они могут характеризоваться гак же, как и жидкости, объемной и поверхностной подвижностью. Времена жизни молекул и атомов на поверхности твердых тел очень сильно различаются для легкоплавких и тугоплавких веществ. Для тугоплавкого вольфрама при комнатной температуре время жизни атомов на поверхности составляет л; Ю32 с. Практическая неподвижность атомов и молекул в тугоплавких телах, хотя они и колеблются около положения равновесия, обусловливает неизменность формы их поверхности во времени. Поверхность твердого тела редко бывает эквипотенциальной. Очевидно, что межфазную поверхность твердое тело — жидкость определяет профиль поверхности твердого тела. Поверхностный слой на межфазных границах имеет одну часть в первой фазе, другую — во второй.
Уравнением (1.1) поверхностная энергия была представлена в виде произведения поверхностного натяжения на площадь поверхности, т. е. соответственно фактора интенсивности на фактор емкости. Рассмотрим несколько подробнее геометрические параметры поверхности. Удельная поверхность тела определяется отношением площади его поверхности Si.2 между фазами 1 и 2 к объему тела V:
Sya = sll2/V (П. І)
Это соотношение будет определять и удельную поверхность дисперсной системы. Общая поверхность между фазами может быть отнесена к дисперсной фазе или к дисперсионной среде.
Рис. ПЛ. Зависимость удельной поверхности 5УД дисперсных систем от размера частиц а и дисперсности D
Обычно при определении удельной поверхности дисперсной системы ее относят к объему дисперсной фазы. Формула (11.1) справедлива для систем с частицами разных и одинаковых размеров.
Дисперсные системы с одинаковыми по размеру частицами дисперсной фазы называются монодисперсными, а с неодинаковыми по размеру частицами — полидисперсными. Реальные системы, как правило, полидисперсны.
Если общие поверхность и объем дисперсной фазы монодисперсной системы выразить через поверхность и объем отдельных частиц (средние значения), то число частиц будет входить и в числитель, и знаменатель уравнения (Н.1). Поэтому удельную поверхность монодисперсной системы можно определить,, зная только размер отдельной частицы.
Например, для систем кубических частиц с размером ребра I и сферических диаметром D имеем:
Sy« = Si,2/K=6f2A3,=6/f, syn = sll2/K=nd2/(V6JK/3)=6/Ј/ (II.2)’
Или в общем виде можно записать
Sya = k/a = kD (II.3)
Где k — коэффициент формы частиц.
Из уравнения (II.3) следует, что удельная поверхность дисперсной системы обратно пропорциональна размеру частиц а и прямо пропорциональна дисперсности D (рис. II.1). Часто удельную поверхность относят к массе т дисперсной фазы (или дисперсионной среды), и тогда необходимо учитывать, плотность вещества р:
SyH = Si,2//rc=s1,z/(Vp) (II.4)’
Для сферических частиц 5уд = 6/(^р).
Изменение удельной поверхности с изменением дисперсности (размера) существенно зависит от формы частиц. Из примеров, приведенных на рис. II.1, при А^>а следует:
ДЛЯ ПЛЄИКН 5уд— 2/У=2Л2/(Л2а)=2/а для бруска sya=sh2/V=4Aa/{Aaz)=4/a (II.5)
Для куба sya = s1,2/V=6a2/a3=6/a
|
|
В этом ряду указанная зависимость увеличивается: возрастает коэффициент формы.
Более конкретной характеристикой дисперсности является кривизна поверхности, определяемая производной площади поверхности по объему:
H^hds/dV (11.1)5
Эту величину удобно применять для характеристики поверхностей неправильной формы. Найдем эту производную для сферической частицы радиусом г.
TOC o "1-3" h z S = 4 яг2; rdr- V=y Зяг3; dV=4 nr2dr ЦІ.7)
Ds 8jt rdr 2 і
DV ^ 4nr*dr = r : r
Для нити цилиндрической формы длиной І имеем:
S = 2ro-f; ds*=2nldrr V=nr4; dV=2nlrdr (II.8)
Ds ^ 2л/ Rfr J_ і
rfV ~ 2rtfrrfr = г ; Я==3 2r
Если частица имеет неправильную форму, то для определения
Кривизны ее поверхности в данной точке пользуются уравнением:
Н^’/,Ч/г{+1/г2) III.9)
Где г, и г2 — радиусы окружностей, полученных при прохождении через поверхность и нормаль к ней в данной точке двух перпендикулярных плоскостей.
Кривизна может быть положительной и отрицательной. Если центр окружности находится внутри тела, кривизна поверхности которого определяется, то она положительна, если центр окружности вне этого тела, то кривизна отрицательна.
При дроблении и измельчении тел увеличивается их удельная поверхность, которая может достигать значительных величин. Расчетные данные табл. II. 1 иллюстрируют резкое возрастание удельной поверхности тела объемом 1 см3 при его измельчении на равновеликие кубики.
Размеры молекул обычно составляют доли нанометра; размеры частиц гетерогенных дисперсных систем могут достигать
Таблица 11.1. Удельная поверхность кубических тел в зависимости от степени измельчения
|
Число частиц |
|
Размер ребра кубика, см |
Удельная поверхность. см2/см3
Единиц нанометра. Таким образом, удельная поверхность может иметь значения, достигающие тысячи квадратных метров на кубический сантиметр (или грамм) дисперсной фазы.
 2 ноября, 2012
2 ноября, 2012  admin
admin 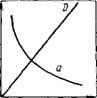
 Опубликовано в рубрике
Опубликовано в рубрике 