Рассмотрим зависимость от расстояния энергии притяжения частиц— молекулярной составляющей расклинивающего давления. Из сил Ван-дер-Ваальса наиболее универсальны и существенны лондоновские силы дисперсионного взаимодействия. Как уже отмечалось, дисперсионное взаимодействие слабо экранируется, поэтому взаимодействие между двумя частицами легко определить суммированием взаимодействий между молекулами или атомами в обеих частицах, например, с помощью интегрирования. Такой приближенный расчет в предположении аддитивности межмолекулярных (межатомных) взаимодействий был проведен де Буром и Гамакером.
Для вывода уравнения энергии молекулярного притяжения между частицами воспользуемся уравнением (III.6) энергии притяжения одной молекулы (атома) к поверхности адсорбента (в данном случае частицы), приведенном в разд. III. А:
£/адс = —яЄ7г/(6*3)
Где С — константа, зависящая/от природы взаимодействующих тел; п — число молекул (атомов) в единице объема частицы.
На рис. VI. 15 показаны две взаимодействующие пластины (как принимается в упрощенном варианте теории ДЛФО), отстоящие на расстоянии h одна от другой. Предположим, что одна молекула (атом) А внутри левой пластины притягивается к правой пластине с энергией U3Дс, рассчитываемой по уравнению (III.6). Расстояние x=r + h, где г — расстояние молекулы (атома) левой пластины от ее поверхности. Чтобы получить энергию молекулярного притяжения пластин, необходимо просуммировать энергии притяжения всех молекул (атомов) левой пластины с правой. Приращение энергии молекулярного притяжения, отнесенное к единице площади пластин, пропорционально приращению числа молекул (атомов) в цилиндре с основанием, равным единице площади, т. е. ndr
Г лПС 1 1
Du^h) = [ — -g—(7+W J ndr (VI •105)
После интегрирования получим:
|
И |
ПпС 1 1 я п*С
— Є + —Щ — (VI.106)
Г=0
Или (/„(A) = — , А12 =. л*п*С (VI. 107)
Из уравнения (VI. J07) видно, что энергия притяжения пластин обратно пропорциональна квадрату расстояния между ни
ми. Это указывает на то, что энергия притяжения между частицами значительно медленнее уменьшается с расстоянием, чем энергия притяжения между молекулами (атомами), которая обратно пропорциональна расстоянию в шестой степени. Отсюда также следует, что частицы дисперсных систем взаимодействуют на более далеких расстояниях, чем молекулы (атомы).
Величина А12 в уравнении (VI. 107) называется константой Гамакера. Она учитывает природу взаимодействующих тел. Эта константа выражается в единицах энергии и имеет значение порядка Ю-19 Дж. Вывод уравнения (VI. 107) проводился в предположении, что пластины находятся в вакууме. При наличии среды константа Ац в уравнении (VI. 107) заменяется на величину
A*—Al+A0 — 2Аоі
Тогда
Ј/M(ft>=—A*/<12jift2> (VI. 108V
Где А н Ао — константы Гамакера для дисперсной фазы, состоящей нз частиц (L) и дисперсионной среды (0) соответственно; Aoi—постоянная взаимодействия фазы н среды.
Чем сильнее взаимодействует дисперсная фаза со средой, тем больше А(И и тем меньше А*, это значит, что силы притяжения между частицами уменьшаются.
Имея отдельные выражения для энергии отталкивания и энергии притяжения частиц, простым сложением получим общую энергию взаимодействия между двумя параллельными пластинами (частицами), приходящуюся на единицу площади. Для области малых потенциалов суммарная энергия взаимодействия равна
|
—xft |
|
(VI. 109) |
|
12яй2 |
А*
U (Ft) — 2е0єх<р2ае
При больших потенциалах и расстояниях между пластинами эта энергия определяется уравнением
|
(ACgRT |
|
А* 12яЛ2 |
|
(VI. 110> |
|
U(h) |
Yie~xh —
|
|
По более сложным уравнениям рассчитываюг энергию взаимодействия сферических частиц. Например, одно из прибли — женных^решений общего уравнения для сферических частиц с низким значением электрического потенциала срв при условии,.
Рис. VI. 15. К выводу уравнения для энергии молекулярного притяжения между пластинами
|
U(hh |
|
|
|
H |
U№
|
|
|
H |
|
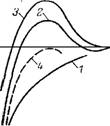
Рис. VI. 17. Потенциальные кривые для дисперсных систем с разной степенью агрегативной устойчивости 1—4 — см. текст |
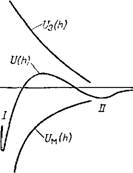
Рис. VI.16. Зависимость энергии электростатического отталкивания U3, Энергии молекулярного притяжения £/м и суммарной энергии взаимодействия частиц (пластин) от расстояния
)
|
(VI.111) |
Что их радиус г значительно больше толщины диффузного слоя 1/х, приводит к следующей формуле:
U(Л) = 2я80егф2д In [1 4- ехр( — Xh)
В соответствии с теорией ДЛФО соотношения (VI. 109) — (VI. 111) определяют поведение дисперсных систем. Их устойчивость или скорость коагуляции зависят от знака и значения общей потенциальной энергии взаимодействия частиц. Положительная энергия отталкивания U3{h) с увеличением расстояния уменьшается по экспоненциальному закону, а отрицательная энергия притяжения /7М (Л) обратно пропорциональна квадрату расстояния (рис. VI.16). В результате на малых расстояниях (при Л-»-0 Ј/3-^const, Uм-*-—о°) и больших расстояниях (экспонента убывает значительно быстрее, чем степенная функция) между частицами преобладает энергия притяжения, а на средних расстояниях — энергия электростатического отталкивания. Первичный минимум I отвечает непосредственному слипанию часїиц, а вторичный минимум II — их притяжению через прослойку среды. Максимум, соответствующий средним расстояниям, характеризует потенциальный барьер, препятствующий слипанию частиц. Силы взаимодействия могут распространяться на расстояния до сотен нанометров, максимальное значение энергии достигает Ю-2 Дж/м2 и более. Увеличению потенциального барьера способствует рост потенциала на поверхности частиц фЛ (VI. 109) в области его малых значений. Эксперименты показывают, что уже при фб^20 мВ возникает потенциальный барьер, обеспечивающий агрегативную устойчивость дис-
перепой системы. Потенциальный барьер увеличивается и с уменьшением константы Гамакера Л*.
Различают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем (рис. VI. 17). Кривая 1 на рис. VI. 17 соответствует такому состоянию дисперсной системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания. Не меняет этого соотношения и тепловое движение частиц. При таком состоянии для дисперсной системы характерна быстрая коагуляция с образованием агрегатов; в системах с жидкой и газообразной дисперсными фазами происходит коалесценция.
Кривая 2 указывает на наличие достаточно высокого потенциального барьера и вторичного минимума. В системе, находящейся в таком состоянии, происходит быстрая флокуляция частиц (перед вторичным минимумом отсутствует потенциальный, барьер) на расстояниях, соответствующих вторичному минимуму. Благодаря же наличию высокого потенциального барьера перед первичным минимумом частицы во флокулах не имеют непосредственного контакта и разделены прослойками среды. Очевидно, что такое состояние отвечает обратимости коагуляции. Пептизация возможна после, .устранения вторичного минимума или уменьшения его до значения ниже кв Т.
Кривая 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии (КвТ). Вероятность образования агрегатов частиц в таких условиях очень мала, и дисперсные системы обладают большой агрегативной устойчивостью.
В упрощенном варианте теории ДЛФО с параллельными пластинами не учитываются размер частиц и их форма. Соотношения, полученные для энергии взаимодействия сферических частиц, показывают [см. уравнение (VI.111)], что’высота ион — но-электростатического барьера и соответственно устойчивость к коагуляции повышаются с увеличением размера частиц. Высота потенциального барьера в первом приближении пропорциональна радиусу частиц. Увеличение размеров — частицы приводит к возрастанию также глубины вторичного энергетического минимума. Это подтверждается тем, что процессы дальней агрегации особенно распространены в грубо’дисперсных системах, например в пастах и цементных растворах. —
С помощью теории ДЛФО получает подтверждение ортоки- петическая коагуляция — прилипание мелких частиц к крупным той же породы. В соответствии с теорией энергия притяжения между крупной частицей (пластиной) и мелкой (сферической) больше, чем между двумя мелкими частицами. Поэтому орто- кинетическая коагуляция не подчиняется уравнению Смолухов — ского для быстрой коагуляции. Теория ДЛФО объясняет ускорение коагуляции в электрическом поле, которое вызывает асимметрию двойного электрического слоя на частицах. На них возникает индуцированный диполь, соответственно появляется дальнодействие, и коагуляция ускоряется.
Электростатическая теория устойчивости дисперсных систем применима к тем системам, устойчивость которых обеспечивается только электростатическим фактором. В реальных же дисперсных системах в лучшем случае возможно преобладающее действие того или иного фактора устойчивости. Однако электростатический фактор устойчивости характерен для наиболее распространенных систем с водными средами, создающими условия для диссоциации. Механизм образования электростатического барьера связан с механизмом образования двойного электрического слоя:поверхностная диссоциация вещества частиц, адсорбция электролитов, в том числе ионогенных ПАВ и ВМС, и ориентирование диполей молекул растворителя или растворенных веществ. Так как электростатический барьер определяется, главным образом, электрическим потенциалом и толщиной двойного электрического слоя (VI. 103), то, очевидно, он будет возрастать с увеличением поверхностной диссоциации, количества адсорбируемых потенциалопределяющих ионов и прочности их закрепления на поверхности частиц, а также с уменьшением взаимодействия противоионов с поверхностью частиц (увеличение толщины двойного слоя). При наличии на поверхности функциональных групп, обладающих слабыми кислотно — основными свойствами, значение электрического потенциала и соответственно потенциального барьера зависит от рН среды. Электролит — стабилизатор должен иметь один ион с достаточным сродством к веществу частицы (чтобы поверхность могла заряжаться), другой — к растворителю (для обеспечения диссоциации электролита — стабилизатора и достаточной толщины двойного слоя).
Как правило,- агрегативная устойчивость дисперсных систем с водной средой повышается по мере увеличения гидратации противоионов в лиотропных рядах ионов: Cs+<Rb+<K+< <Na+<Li+ и 1~<Вг~<С1-. Необходимо учитывать, что наличие индифферентных электролитов в дисперсной системе снижает толщину диффузной части двоййого слоя 1/х на частицах и соответственно электрический потенциал (11.124). Органические стабилизаторы — ионогенные ПАВ и ВМС в водных средах обычно ориентируются органическими радикалами к частице, а ионогенной группой — к воде, что обеспечивает диссоциацию функциональной группы, появление электрического потенциала па поверхности частиц и соответственно агрегативную устойчивость дисперсной системы.
 2 ноября, 2012
2 ноября, 2012  admin
admin 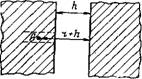
 Опубликовано в рубрике
Опубликовано в рубрике 