Как показано выше, устойчивость дисперсных систем и коагуляция отражают непосредственно взаимодействие частиц дисперсной фазы между собой или с какими-либо макроповерхностями, Это взаимодействие также определяет адгезию частиц к макроповерхностям и структурообразование в дисперсных системах. Поэтому в основе любой теории устойчивости, учитывающей механизм этих взаимодействий, должно лежать соотношение между силами притяжения и отталкивания частиц. Существует единое мнение в отношении природы сил притяжения, которые обусловлены межмолекулярными ван-дер-ваальсо — выми силами. Силы же отталкивания между частицами могут иметь разную природу, соответствующую факторам устойчивости. Предложено несколько теорий устойчивости и коагуляции, объясняющих те или иные экспериментальные факты с различных позиций (Дюкло, Фрейндлих, Мюллер, Рабинович, Оствальд и др.). Однако все эти теории односторонние, они не учитывают и не объясняют многие факты.
Широкое признание и распространение получила теория устойчивости и коагуляции, учитывающая — злвктростатиЧескую со— стявляющУот рЯгклиниияютпего давления (отталкивание) и его молекулярную составляющую (притяжение). Эта теория удов»-— леТворитёльно описывает закономерности поведения типично лиофобных дисперсных систем, для которых можно пренебречь адсорбционио-сольватным фактором устойчивости.
В наиболее общем виде эта теория была разработана советскими учеными Б. В. Дерягиным и Л. Д. Ландау в 1937—1941 гг. и несколько позднее независимо от них голландскими учеными Фервеем и Овербеком; по первым буквам фамилий этих ученых теория названа теорией ДЛФО. Теорию ДЛФО часто называют физической теорией. Если подходить к ее оценке с позиций химии, то будет правомерным отнести ее к кинетической теории, так как она рассматривает процесс взаимодействия частиц по отдельным стадиям — перекрывание их поверхностных слоев и возникновение расклинивающего давления, используя при этом понятие потенциального барьера, аналогичное энергии активации в химической кинетике.
Чтобы получить представление о сущности этой теории и ее следствиях, рассмотрим простейший вариант взаимодействия крупных частиц, для которых можно не учитывать теплового движения. Взаимодействие крупных частиц можно рассматривать как взаимодействие между двумя плоскими параллельными пластинами, т. е. принять, что линейный размер частиц значительно больше толщины двойного электрического слоя.
Общая энергия взаимодействия между двумя пластинами, приходящаяся на единицу их площади, равна
U=U3+UM (VI.93)
Где U—J и Uм»—энергия электростатического отталкивания и молекулярного притяжения соответственно.
Каждую из этих энергий можно выразить как функцию от расстояния H между пластинами:
<Шэ=Пэ£Й (VI.94)
DUM=Tludh (VI.95)
Где Пэ — давление отталкивания, в данном случае электростатическая составляющая расклинивающего давления; Пм — давление притяжения, т. е. молекулярная составляющая расклинивающего давления.
Давление Пи обусловлено обычно стремлением системы к уменьшению поверхностной энергии, его природа связана с ван- дер-ваальсовыми силами.
В теории ДЛФО (в ее классическом виде) принято, что давление отталкивания обусловлено только электростатическими силами, поэтому s
— </1Тэ=Р£/(р . (VI.96)
Где р’— объемная плотность заряда в двойном электрическом слое; ф 1— электрический потенциал двойного слоя.
Наиболее точное описание распределения объемной плотности заряда в двойном электрическом слое дает теория Штерна. Для упрощения вывода зависимости энергии отталкивания от расстояния предполагают, что при взаимодействии пластин происходит деформация только диффузной части двойного электрического слоя, поэтому можно воспользоваться теорией Гуи — Чепмена. Ограничимся условием, ісогда потенциал q> имеет малое значение, и его изменение следует приведенному ранее уравнению (11.124):
Ф* = фвЄ-ю:
Где фа — потенциал диффузной части двойного электрического слоя; х — величина, обратная толщине диффузной части двойного слоя.
|
Рис. VI.14. Схема, показывающая изменение электрического потенциала между двумя одноименно заряженными частицами (пластинами) прн непе — рекрытых (а) и перекрытых (б) двойных электрических слоях |
Если пластины (частицы) находятся на расстоянии h = 2x, На котором взаимодействия не происходит (рис. VI. 14, а), то двойные электрические слои не перекрываются, и потенциалы в них снижаются практически до нуля (<р = 0). При сближении пластин двойные электрические слои перекрываются, и соотношение (11.124) может быть применено только для описания области, близкой к поверхности пластин (рис. VI. 14, б). Принимают, что в середине расстояния между пластинами в результате взаимодействия двойных слоев потенциал становится равным 2ф*, т. е. распределение потенциала происходит в соответствии со сплошной кривой на рис. VI. 14, б.
‘ Таким образом, для определения электростатической составляющей расклинивающего давления интегрирование уравнения (VI.96) необходимо провести в пределах области снижения потенциала при отталкивании пластин, т. е. от до нуля:
О
Pdcp (VI.97)
2<Px
Сопоставляя уравнение Пуассона (11.113) с соотношением Пуассона — Больцмана при малом значении потенциала (11.118)
D2q>/dx2=— p/ієое), d./dx2=K
Получим, что
Р=_еоЄх2ф (VI.98)
Подставляя это выражение для р в (VI.97), найдем:
Пэ е= І" е0ех! ф гіф =) 2е0ех*ф*х (VI .99)
О
Учитывая уравнение (11.124) и что ft = 2х, получим зависимость электростатической составляющей расклинивающего давления от расстояния в области низких потенциалов:
IT, = 2P(>F х2г("2лв_ *H (VI.100)
Если провести подобный вывод для области высоких потенциалов и больших расстояний между пластинами, то уравнение электростатической составляющей расклинивающего давления примет следующий вид:
П,=64с0ЯГ^-‘"1 (VI.101)
|
Exp[zF(pg/(2RT) ] |
Ехр[гґ<р6/(2/?Г)]- 1
Где у.
Со — концентрация противоионов в растворе; z— заряд противоионов; F — число Фарадея.
Следует отметить, что электростатическая составляющая расклинивающего давления в области малых потенциалов (VI.100) сильно зависит от значения потенциала (пропорционально ф»2), с ростом же потенциала эта зависимость становится менее заметной. При больших значениях <рв потенциал перестает влиять на расклинивающее давление отталкивания. Это можно объяснить тем, что с ростом потенциала одновременно увеличивается притяжение противоионов двойного электрического слоя к поверхности, эффективный заряд которой поэтому почти не изменяется.
Чтобы получить выражение для энергии электростатического отталкивания пластин, интегрируем уравнение (VI.94) в пределах от ft до оо после подстановки в него соотношения (VI. 100):
ОО оо СО
Иэ J" Пэ dh t= J 2E0Sx2Q>52E—Xft<M 2g°e^p2a J e-*hd(-Y.h) (VI. 102) H h h Окончательно имеем:
V, (ft) = 2єое>с(р v-"1 (VI. 103)
При больших значениях потенциалов аналогичное интегрирование уравнения (VI.94) после подстановки соотношения (VI. 101) приводит к выражению
U9(h)=Z*EЈLfe-* (VI. 104):
Таким образом, энергия отталкивания частиц, как и электростатическая составляющая расклинивающего давления, возрастает с уменьшением расстояния Л между ними по экспоненциальному закону.
 2 ноября, 2012
2 ноября, 2012  admin
admin 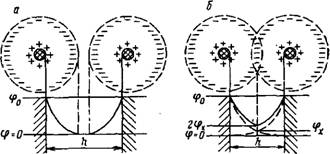
 Опубликовано в рубрике
Опубликовано в рубрике 